evaluare | Biopsihologie | comparativă |cognitivă | dezvoltare | limbă | diferențe individuale |personalitate | filozofie | socială |
metode | statistici |articole clinice | educaționale | industriale |profesionale |Psihologie Mondială |
statistici:metodă științifică · metode de cercetare · proiectare experimentală · cursuri de Statistică universitare · teste statistice · teoria jocurilor · teoria deciziei
vă rugăm să ajutați la îmbunătățirea acestei pagini dacă puteți..
analiza Cluster sau clustering este o tehnică comună pentru analiza datelor statistice, care este utilizată în multe domenii, inclusiv învățarea automată, extragerea datelor, recunoașterea modelelor, analiza imaginilor și bioinformatica. Clustering este clasificarea obiectelor similare în grupuri diferite sau, mai precis, Partiționarea unui set de date în subseturi (clustere), astfel încât datele din fiecare subset (în mod ideal) împărtășesc o trăsătură comună – adesea proximitate în funcție de o anumită măsură de distanță definită.
pe lângă termenul de clustering de date (sau doar clustering), există o serie de termeni cu semnificații similare, inclusiv analiza clusterului, clasificarea automată, taxonomia numerică, botriologia și analiza tipologică.
- tipurile de clustering
- gruparea ierarhică
- măsurarea distanței
- crearea clusterelor
- grupare ierarhică aglomerată
- grupare Partițională
- K-înseamnă și derivate
- K-înseamnă grupare
- algoritmul Qt Clust
- Fuzzy c-înseamnă clustering
- criteriul cotului
- clustering Spectral
- Aplicații
- Biologie
- cercetare de Marketing
- alte aplicații
- comparații între clusterings de date
- a se vedea, de asemenea,
- Bibliografie
- implementări Software
- gratuit
tipurile de clustering
algoritmii de clustering a datelor pot fi ierarhici sau partiționali. Algoritmii ierarhici găsesc clustere succesive folosind clustere stabilite anterior, în timp ce algoritmii partiționali determină toate clusterele simultan. Algoritmii ierarhici pot fi aglomerați (de jos în sus) sau divizivi (de sus în jos). Algoritmii aglomerați încep cu fiecare element ca un cluster separat și le îmbină în clustere succesiv mai mari. Algoritmii divizori încep cu întregul set și continuă să-l împartă în clustere succesiv mai mici.
gruparea ierarhică
măsurarea distanței
un pas cheie într-o grupare ierarhică este selectarea unei măsurători a distanței. O măsură simplă este distanța manhattan, egală cu suma distanțelor absolute pentru fiecare variabilă. Numele provine din faptul că într-un caz cu două variabile, variabilele pot fi reprezentate grafic pe o grilă care poate fi comparată cu străzile orașului, iar distanța dintre două puncte este numărul de blocuri pe care o persoană le-ar parcurge.
o măsură mai comună este distanța euclidiană, calculată prin găsirea pătratului distanței dintre fiecare variabilă, însumarea pătratelor și găsirea rădăcinii pătrate a acelei sume. În cazul cu două variabile, distanța este analogă cu găsirea lungimii ipotenuzei într-un triunghi; adică este distanța „pe măsură ce zboară cioara.”O revizuire a analizei clusterului în cercetarea psihologiei sănătății a constatat că cea mai comună măsură a distanței în studiile publicate în acea zonă de cercetare este distanța euclidiană sau distanța euclidiană pătrată.
crearea clusterelor
având în vedere o măsură de distanță, elementele pot fi combinate. Gruparea ierarhică construiește (aglomerativă) sau se desparte (divizivă), o ierarhie a clusterelor. Reprezentarea tradițională a acestei ierarhii este o structură de date arbore (numită dendrogramă), cu elemente individuale la un capăt și un singur cluster cu fiecare element la celălalt. Algoritmii aglomerativi încep în partea de sus a arborelui, în timp ce algoritmii divizori încep în partea de jos. (În figură, săgețile indică o grupare aglomerată.)
tăierea copacului la o înălțime dată va da o grupare la o precizie selectată. În exemplul următor, tăierea după al doilea rând va produce clustere {A} {b c} {d E} {f}. Tăierea după al treilea rând va produce clustere {A} {b c} {d E f}, care este o grupare mai grosieră, cu un număr mai mic de clustere mai mari.
grupare ierarhică aglomerată
de exemplu, să presupunem că aceste date vor fi grupate. Unde distanța euclidiană este metrica distanței.
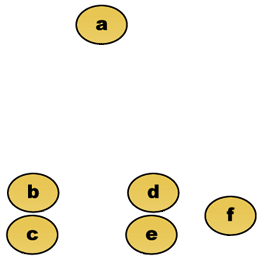
date brute
dendrograma ierarhică de grupare ar fi ca atare:
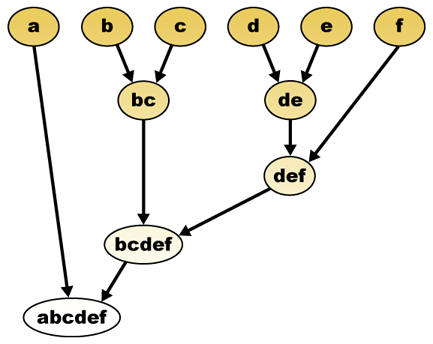
reprezentare tradițională
această metodă construiește ierarhia din elementele individuale prin îmbinarea progresivă a clusterelor. Din nou, avem șase elemente {A} {B} {c} {d} {e} și {f}. Primul pas este de a determina ce elemente să fuzioneze într-un cluster. De obicei, vrem să luăm cele două elemente cele mai apropiate, de aceea trebuie să definim o distanță 
să presupunem că am îmbinat cele două elemente cele mai apropiate b și c, acum avem următoarele clustere {A}, {B, C}, {d}, {E} și {F} și dorim să le îmbinăm mai departe. Dar pentru a face asta, trebuie să luăm distanța dintre {a} și {b c} și, prin urmare, să definim distanța dintre două clustere. De obicei, distanța dintre două clustere 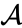
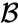
- distanța maximă dintre elementele fiecărui cluster (numită și clustering complet de legătură):
- distanța minimă dintre elementele fiecărui cluster (numită și clustering cu o singură legătură):
- distanța medie dintre elementele fiecărui cluster (numită și clustering mediu de legătură):
- suma tuturor varianței intra-cluster
- creșterea varianței pentru clusterul fuzionat (criteriul Ward)
- probabilitatea ca clusterele candidate să apară din aceeași funcție de distribuție (v-linkage)
fiecare aglomerare are loc la o distanță mai mare între clustere decât aglomerarea anterioară și se poate decide oprirea grupării fie atunci când clusterele sunt prea îndepărtate pentru a fi îmbinate (criteriul distanței) sau atunci când există un număr suficient de mic de clustere (criteriul numărului).
grupare Partițională
K-înseamnă și derivate
K-înseamnă grupare
algoritmul K-înseamnă atribuie fiecare punct clusterului al cărui centru (numit și centroid) este cel mai apropiat. Centrul este media tuturor punctelor din cluster-adică coordonatele sale sunt media aritmetică pentru fiecare dimensiune separat pe toate punctele din cluster.
exemplu: Setul de date are trei dimensiuni, iar clusterul are două puncte: X = (x1, x2, x3) și Y = (y1, y2, y3). Apoi centroidul Z devine Z = (z1, z2, z3), unde z1 = (x1 + y1)/2 și z2 = (x2 + y2)/2 și z3 = (x3 + y3)/2.
algoritmul este aproximativ (J. MacQueen, 1967):
- genera aleatoriu k clustere și de a determina centrele de cluster, sau de a genera direct K puncte de semințe ca centre de cluster.
- alocați fiecare punct celui mai apropiat centru de cluster.
- recalculați noile centre de cluster.
- repetați până când este îndeplinit un criteriu de convergență (de obicei că atribuirea nu s-a schimbat).
principalele avantaje ale acestui algoritm sunt simplitatea și viteza care îi permit să ruleze pe seturi de date mari. Dezavantajul său este că nu produce același rezultat cu fiecare rulare, deoarece clusterele rezultate depind de sarcinile aleatorii inițiale. Maximizează varianța inter-cluster (sau minimizează intra-cluster), dar nu asigură că rezultatul are un minim global de varianță.
algoritmul Qt Clust
gruparea Qt (prag de calitate) (Heyer și colab., 1999) este o metodă alternativă de partiționare a datelor, inventată pentru gruparea genelor. Necesită mai multă putere de calcul decât mijloacele k, dar nu necesită specificarea numărului de clustere a priori și returnează întotdeauna același rezultat atunci când rulează de mai multe ori.
algoritmul este:
- utilizatorul alege un diametru maxim pentru clustere.
- construiți un cluster candidat pentru fiecare punct incluzând cel mai apropiat punct, următorul cel mai apropiat și așa mai departe, până când diametrul clusterului depășește pragul.
- Salvați clusterul candidat cu cele mai multe puncte ca primul cluster adevărat și eliminați toate punctele din cluster de la o analiză suplimentară.
- se repetă cu setul redus de puncte.
distanța dintre un punct și un grup de puncte este calculată folosind legătura completă, adică. ca distanța maximă de la punct la orice membru al grupului (a se vedea secțiunea „clustering ierarhic aglomerat” despre distanța dintre clustere).
Fuzzy c-înseamnă clustering
în clustering fuzzy, fiecare punct are un grad de apartenență la clustere, ca în logica fuzzy, mai degrabă decât să aparțină complet unui singur cluster. Astfel, punctele de pe marginea unui cluster pot fi în cluster într-o măsură mai mică decât punctele din Centrul clusterului. Pentru fiecare punct x avem un coeficient care dă gradul de a fi în KTH cluster 

cu C-mijloace fuzzy, centroidul unui cluster este media tuturor punctelor, ponderate de gradul lor de apartenență la cluster:
gradul de apartenență este legat de inversul distanței față de cluster
apoi coeficienții sunt normalizați și fuzionați cu un parametru real 
pentru m egal cu 2, Aceasta este echivalentă cu normalizarea coeficientului liniar pentru a face suma lor 1. Când m este aproape de 1, atunci Centrul de cluster cel mai apropiat de punct este dat mult mai multă greutate decât celelalte, iar algoritmul este similar cu K-înseamnă.
algoritmul fuzzy c-means este foarte similar cu algoritmul k-means:
- alegeți un număr de clustere.
- atribuie aleatoriu fiecărui punct coeficienți pentru a fi în clustere.
- repetați până când algoritmul a convergent (adică schimbarea coeficienților între două iterații nu este mai mare de
, pragul de sensibilitate dat) :
- calculați centroidul pentru fiecare cluster, folosind formula de mai sus.
- pentru fiecare punct, calculați coeficienții săi de a fi în clustere, folosind formula de mai sus.
algoritmul minimizează și varianța intra-cluster, dar are aceleași probleme ca și mijloacele k, minimul este un minim local, iar rezultatele depind de alegerea inițială a greutăților.
criteriul cotului
criteriul cotului este o regulă comună pentru a determina ce număr de clustere ar trebui alese, de exemplu pentru k-means și clustering ierarhic aglomerat.
criteriul cotului spune că ar trebui să alegeți un număr de clustere, astfel încât adăugarea unui alt cluster să nu adauge suficiente informații. Mai exact, dacă graficați procentul de varianță explicat de clustere în raport cu numărul de clustere, primele clustere vor adăuga multe informații (explicați o mulțime de varianță), dar la un moment dat câștigul marginal va scădea, oferind un unghi în grafic (cotul).
în graficul următor, cotul este indicat de cercul roșu. Prin urmare, numărul de clustere alese ar trebui să fie 4.
clustering Spectral
având în vedere un set de puncte de date, matricea de similitudine poate fi definită ca o matrice


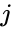
o astfel de tehnică este algoritmul Shi-Malik, utilizat în mod obișnuit pentru segmentarea imaginilor. Împarte punctele în două seturi 


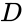
această partiționare se poate face în diferite moduri, cum ar fi luând mediana 



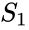
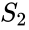
un algoritm înrudit este algoritmul Meila-Shi, care ia vectorii proprii corespunzători celor mai mari valori proprii k ale matricei 
Aplicații
Biologie
în biologie clustering are multe aplicații în domeniile biologiei computaționale și bioinformatică, dintre care două sunt:
- în transcriptomică, gruparea este utilizată pentru a construi grupuri de gene cu modele de Expresie conexe. Adesea, astfel de grupuri conțin proteine legate funcțional, cum ar fi enzimele pentru o cale specifică sau genele care sunt co-reglementate. Experimentele cu randament ridicat folosind etichete de secvență exprimate (Est) sau microarrays ADN pot fi un instrument puternic pentru adnotarea genomului, un aspect general al genomicii.
- în analiza secvențelor, gruparea este utilizată pentru a grupa secvențele omoloage în familii de gene. Acesta este un concept foarte important în bioinformatică și în biologia evoluționistă în general. A se vedea evoluția prin duplicarea genelor.
cercetare de Marketing
analiza Cluster este utilizată pe scară largă în cercetarea de piață atunci când se lucrează cu date multivariate din sondaje și panouri de testare. Cercetătorii de piață folosesc analiza cluster pentru a împărți populația generală a consumatorilor în segmente de piață și pentru a înțelege mai bine relațiile dintre diferite grupuri de consumatori/potențiali clienți.
- segmentarea pieței și determinarea piețelor țintă
- poziționarea produsului
- dezvoltarea de produse noi
- selectarea piețelor de testare (a se vedea : tehnici experimentale)
alte aplicații
analiza rețelelor sociale: în studiul rețelelor sociale, gruparea poate fi utilizată pentru a recunoaște comunitățile din grupuri mari de oameni.
segmentarea imaginii: gruparea poate fi utilizată pentru a împărți o imagine digitală în regiuni distincte pentru detectarea frontierelor sau recunoașterea obiectelor.
data mining: multe aplicații de data mining implică partiționarea elementelor de date în subseturi conexe; aplicațiile de marketing discutate mai sus reprezintă câteva exemple. O altă aplicație comună este împărțirea documentelor, cum ar fi paginile World Wide Web, în genuri.
comparații între clusterings de date
au existat mai multe sugestii pentru o măsură de similitudine între două clusterings. O astfel de măsură poate fi utilizată pentru a compara cât de bine funcționează diferiți algoritmi de grupare a datelor pe un set de date. Multe dintre aceste măsuri sunt derivate din matricea de potrivire (aka matricea de confuzie), de exemplu, măsura Rand și măsurile Fowlkes-Mallows BK.
- Jain, Murty și Flynn: Clustering de date: o revizuire, ACM Comp. Surv., 1999. Disponibil aici.
- pentru o altă prezentare a mijloacelor ierarhice, k și a mijloacelor c neclare, consultați această introducere în clustering. De asemenea, are o explicație pe amestec de Gaussians.
- David Dowe, pagina de modelare a amestecului – alte legături de grupare și model de amestec.
- un tutorial despre clustering
- manualul on-line: Teoria informației, inferența și algoritmii de învățare, de David J. C. MacKay include capitole despre K-înseamnă clustering, soft K-înseamnă clustering și derivări, inclusiv algoritmul E-M și viziunea variațională a algoritmului E-M.
a se vedea, de asemenea,
- k-înseamnă
- rețea neuronală artificială (ANN)
- hartă auto-organizare
- maximizarea așteptărilor (EM)
Bibliografie
- Clatworthy, J., Buick, D., Hankins, M., Weinman, J., & Horne, R. (2005). Utilizarea și raportarea analizei clusterului în psihologia sănătății: o revizuire. Jurnalul britanic de Psihologie a sănătății 10: 329-358.
- Romesburg, H. Clarles, analiza clusterului pentru cercetători, 2004, 340 pp. ISBN 1411606175 sau editor, retipărirea ediției din 1990 publicată de Krieger Pub. Co… O traducere în limba japoneză este disponibilă de la Uchida Rokakuho Publishing Co., Ltd., Tokyo, Japonia.
- Heyer, L. J., Kruglyak, S. și Yooseph, S., Explorarea datelor de Expresie: identificarea și analiza genelor Coexprimate, cercetarea genomului 9:1106-1115.
- manualul on-line: Teoria informației, inferența și algoritmii de învățare, de David J. C. MacKay include capitole despre K-înseamnă clustering, soft K-înseamnă clustering și derivări, inclusiv algoritmul E-M și viziunea variațională a algoritmului E-M.
pentru gruparea spectrală :
- Jianbo Shi și Jitendra Malik, „Reduceri normalizate și segmentarea imaginilor”, tranzacții IEEE privind Analiza modelelor și inteligența mașinilor, 22(8), 888-905, August 2000. Disponibil pe pagina de pornire a Jitendra Malik
- Marina Meila și Jianbo Shi, „segmentarea învățării cu plimbare aleatorie”, Neural Information Processing Systems, NIPS, 2001. Disponibil de pe pagina de pornire Jianbo Shi
pentru estimarea numărului de clustere:
- Can, F., Ozkarahan, E. A. (1990) ” conceptele și eficacitatea metodologiei de clustering bazate pe coeficienți de acoperire pentru bazele de date text.”Tranzacții ACM pe sisteme de baze de date. 15 (4) 483-517.
implementări Software
gratuit
- pachetul flexclust pentru R
- YALE (încă un alt mediu de învățare): software gratuit open-source pentru descoperirea de cunoștințe și data mining, inclusiv, de asemenea, un plugin pentru clustering
- unele fișiere sursă Matlab pentru clustering aici
- compact – pachet comparativ pentru evaluarea clustering (de asemenea, în Matlab)
- mixmod : Clusterul Bazat Pe Model Și Analiza Discriminantă. Cod în C++, Interfață cu Matlab și Scilab
- LingPipe Clustering Tutorial Tutorial pentru a face complet – și single-link clustering folosind LingPipe, un pachet Java Data mining text distribuit cu sursa.
- Weka : Weka conține instrumente pentru pre-procesarea datelor, clasificarea, regresia, gruparea, regulile de asociere și vizualizarea. De asemenea, este potrivit pentru dezvoltarea de noi scheme de învățare automată.