dzisiaj będzie krótkie wprowadzenie do statystyki cyrkulacyjnej (czasami określane jako statystyki kierunkowe). Statystyka kołowa jest interesującym podziałem statystyki obejmującym obserwacje podejmowane jako wektory wokół okręgu jednostkowego. Jako przykład, wyobraź sobie pomiar czasu porodu w szpitalu w ciągu 24-godzinnego cyklu lub kierunkowe rozproszenie grupy wędrownych zwierząt. Ten rodzaj danych dotyczy różnych dziedzin, takich jak Ekologia, klimatologia i biochemia. Charakter obserwacji pomiarowych wokół okręgu jednostkowego wymaga innego podejścia do badania hipotez. Rozkłady muszą być „owinięte” wokół okręgu, aby były użyteczne, a konwencjonalne estymatory, takie jak średnia próbki lub wariancja próbki, nie zawierają wody.
w tym poście przeprowadzimy Test odstępów Rao w celu oceny jednorodności okrągłego zbioru danych. Jest to podstawowa procedura i powinna być traktowana jako wprowadzenie do obsługi danych o obiegu zamkniętym.
pierwsze kroki
przeprowadzimy Test hipotezy na żółwiach, mały zbiór danych składający się z kątów przybycia 10 zielonych żółwi morskich na ich wyspę lęgową. Naszym celem jest określenie, gdzie kąty przylotów wykazują oznaki kierunkowości lub są bardziej wskazujące na przypadkowe rozproszenie.
najpierw zainstaluj pakiet circular i dołącz zestaw danych żółwi.
install.packages("circular")require(circular)attach(turtles)
wykreślanie danych
pakiet circularzawiera własną funkcję wykreślania, plot.circular. Przyjrzyjmy się kątom przybycia żółwi.
plot.circular(arrival)
oto wykres: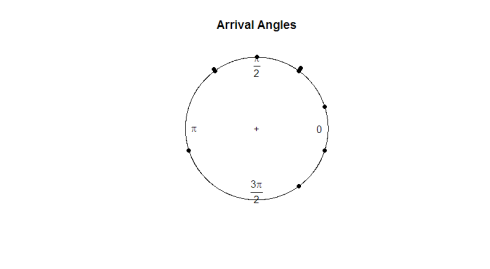
biorąc pod uwagę badanie oczu, obserwacje wydają się być jednolite wokół okręgu. Jeśli chcemy uruchomić Test hipotezy, aby określić, czy dane są naprawdę jednolite, będziemy musieli opracować statystykę testową, która działa z danymi kątowymi.
jaki jest dobry parametr do wykorzystania? Pobranie średniej próby nie mówi nam wiele o kierunku danych(180 stopni nie jest użyteczną średnią 2 stopni i 358 stopni). Na poniższym wykresie, obserwuj, jak średnia próby jest bezużyteczna w reprezentowaniu kształtu lub rozprzestrzeniania się naszych danych.
mean(arrival)plot.circular(mean(arrival)) 0.9120794
oto fabuła: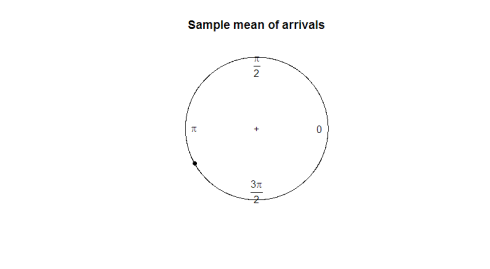
zamiast tego użyjemy metody, która określa kierunkowość, mierząc średnią przestrzeń między obserwacjami. Test ten nazywa się testem odstępów Rao.
Test odstępu Rao
Test odstępu Rao został opracowany w celu oceny jednolitości danych kołowych. Wykorzystuje przestrzeń między obserwacjami, aby określić, czy dane wykazują znaczącą kierunkowość. Jeśli dane są jednolite, obserwacje powinny być równomiernie rozmieszczone.
oto statystyka testu \(U\) Dla testu odstępów Rao: $$U = 1/2\sum\limits_{i=1}^n |T_{i} – λ| $$ gdzie \(λ = 360/n, T_{i} = f_{i+1}-f_{i}\) i \(t_{n} = (360-f_{n})+f_{1}\)
zasadniczo statystyka badania agreguje odchylenia między kolejnymi punktami, z których każdy ważony jest całkowitą liczbą obserwacji w zbiorze danych.
użyjemy funkcji rao.spacing.test()do uruchomienia tego testu hipotez. Nasza hipoteza zerowa mówi, że dane mają jednolity rozkład, podczas gdy stany alternatywne dane wykazują oznaki kierunkowości. Zróbmy test.
rao.spacing.test(arrival,alpha=.10) Rao's Spacing Test of Uniformity Test Statistic = 127.2689 Level 0.1 critical value = 161.23 Do not reject null hypothesis of uniformity
przy statystykach testu 127 spadających poniżej wartości krytycznej 161 dane nie ulegają znacznemu pochyleniu w żadnym kierunku. Nie możemy odrzucić hipotezy, że żółwie przybywające mają jednolity rozkład.
wniosek
test odstępów Rao ustalił, że dane nie wykazują oznak trendów kierunkowych. Nie możemy odrzucić hipotezy zerowej jednolitości i przyjmiemy jednolitość w odniesieniu do kierunku przybycia. Chociaż ten post był stosunkowo prostym samouczkiem, Wiele osób ze społeczności data science nie pracowało wcześniej z danymi okrągłymi. Jest to ciekawa Subtopia do nurkowania, a także młoda dziedzina statystyki, która wciąż się rozwija.
Uwagi końcowe
chciałbym rozszerzyć uznanie dla S. Rao Jammalamadaka PhD, z Uniwersytetu Kalifornijskiego w Santa Barbara, i jego podręcznika „Topics in Circular Statistics” za wywołanie mojego zainteresowania w dziedzinie statystyki cyrkulacyjnej.