4.2 Szacowanie współczynników modelu regresji liniowej
w praktyce punkt przecięcia \(\beta_0\) i nachylenie \(\beta_1\) linii regresji populacyjnej nie są znane. Dlatego musimy wykorzystać dane do oszacowania zarówno nieznanych parametrów. W poniższym przykładzie przedstawimy, w jaki sposób można to osiągnąć. Chcemy powiązać wyniki testów ze wskaźnikami uczeń-nauczyciel mierzonymi w kalifornijskich szkołach. Wynik testu jest średnią ocen czytelniczych i matematycznych dla piątoklasistów. Ponownie, wielkość klasy jest mierzona jako liczba uczniów podzielona przez liczbę nauczycieli (stosunek uczeń-nauczyciel). Jeśli chodzi o Dane, California School data set (CASchools) jest dostarczany z pakietem r o nazwie AER, akronimem dla Stosowanej Ekonometrii z R (Kleiber and Zeileis 2020). Po zainstalowaniu pakietu z install.Pakiety („AER”) i dołączając je do biblioteki(AER) zbiór danych można załadować za pomocą funkcji data ().
## # install the AER package (once)## install.packages("AER")## ## # load the AER packagelibrary(AER)# load the the data set in the workspacedata(CASchools)po zainstalowaniu pakietu jest on dostępny do użytku przy kolejnych okazjach, gdy jest wywoływany z library () – nie ma potrzeby uruchamiania install.packages () ponownie!
ciekawe, z jakim przedmiotem mamy do czynienia.class () zwraca klasę obiektu. W zależności od klasy obiektu niektóre funkcje (na przykład plot () i summary ()) zachowują się inaczej.
sprawdźmy klasę obiektu CASchools.
class(CASchools)#> "data.frame"okazuje się, że CASchools jest klasą danych.ramka, która jest wygodnym formatem do pracy, szczególnie do wykonywania analizy regresji.
z pomocą funkcji head() otrzymujemy pierwszy przegląd naszych danych. Ta funkcja pokazuje tylko pierwsze 6 wierszy zestawu danych, co zapobiega przepełnionemu wyjściu konsoli.
head(CASchools)#> district school county grades students teachers#> 1 75119 Sunol Glen Unified Alameda KK-08 195 10.90#> 2 61499 Manzanita Elementary Butte KK-08 240 11.15#> 3 61549 Thermalito Union Elementary Butte KK-08 1550 82.90#> 4 61457 Golden Feather Union Elementary Butte KK-08 243 14.00#> 5 61523 Palermo Union Elementary Butte KK-08 1335 71.50#> 6 62042 Burrel Union Elementary Fresno KK-08 137 6.40#> calworks lunch computer expenditure income english read math#> 1 0.5102 2.0408 67 6384.911 22.690001 0.000000 691.6 690.0#> 2 15.4167 47.9167 101 5099.381 9.824000 4.583333 660.5 661.9#> 3 55.0323 76.3226 169 5501.955 8.978000 30.000002 636.3 650.9#> 4 36.4754 77.0492 85 7101.831 8.978000 0.000000 651.9 643.5#> 5 33.1086 78.4270 171 5235.988 9.080333 13.857677 641.8 639.9#> 6 12.3188 86.9565 25 5580.147 10.415000 12.408759 605.7 605.4okazuje się, że zbiór danych składa się z wielu zmiennych i że większość z nich jest numeryczna.
przy okazji: alternatywą dla class() I head () jest str (), która jest wyprowadzona z 'struktury’ i daje kompleksowy przegląd obiektu. Spróbuj!
Wracając do CASchools, dwie zmienne, którymi jesteśmy zainteresowani (tj., średni wynik testu i stosunek uczeń-nauczyciel) nie są uwzględniane. Jednak możliwe jest obliczenie zarówno z dostarczonych danych. Aby uzyskać stosunek uczeń-nauczyciel, po prostu dzielimy liczbę uczniów przez liczbę nauczycieli. Średni wynik testu to średnia arytmetyczna wyniku testu do czytania i wynik testu z matematyki. Następny fragment kodu pokazuje, jak dwie zmienne mogą być konstruowane jako wektory i jak są dołączane do CASchools.
# compute STR and append it to CASchoolsCASchools$STR <- CASchools$students/CASchools$teachers # compute TestScore and append it to CASchoolsCASchools$score <- (CASchools$read + CASchools$math)/2 jeśli uruchomimy head (CASchools) ponownie, znajdziemy dwie interesujące zmienne jako dodatkowe kolumny o nazwie STR i score(sprawdź to!).
tabela 4.1 z podręcznika podsumowuje rozkład wyników testów i proporcje uczeń-nauczyciel. Istnieje kilka funkcji, które można wykorzystać do uzyskania podobnych wyników, np.,
-
średnia () (oblicza średnią arytmetyczną podanych liczb),
-
sd () (Oblicza odchylenie standardowe próbki),
-
quantile () (zwraca wektor podanych przykładowych kwantyli dla danych).
następny fragment kodu pokazuje, jak to osiągnąć. Najpierw obliczamy statystyki sumaryczne na kolumnach STR i wynik CASchools. Aby uzyskać dobre wyniki, zbieramy miary w danych.ramka o nazwie DistributionSummary.
# compute sample averages of STR and scoreavg_STR <- mean(CASchools$STR) avg_score <- mean(CASchools$score)# compute sample standard deviations of STR and scoresd_STR <- sd(CASchools$STR) sd_score <- sd(CASchools$score)# set up a vector of percentiles and compute the quantiles quantiles <- c(0.10, 0.25, 0.4, 0.5, 0.6, 0.75, 0.9)quant_STR <- quantile(CASchools$STR, quantiles)quant_score <- quantile(CASchools$score, quantiles)# gather everything in a data.frame DistributionSummary <- data.frame(Average = c(avg_STR, avg_score), StandardDeviation = c(sd_STR, sd_score), quantile = rbind(quant_STR, quant_score))# print the summary to the consoleDistributionSummary#> Average StandardDeviation quantile.10. quantile.25. quantile.40.#> quant_STR 19.64043 1.891812 17.3486 18.58236 19.26618#> quant_score 654.15655 19.053347 630.3950 640.05000 649.06999#> quantile.50. quantile.60. quantile.75. quantile.90.#> quant_STR 19.72321 20.0783 20.87181 21.86741#> quant_score 654.45000 659.4000 666.66249 678.85999jeśli chodzi o przykładowe dane, używamy plot (). Pozwala nam to wykryć cechy naszych danych, takie jak wartości odstające, które są trudniejsze do wykrycia, patrząc na zwykłe liczby. Tym razem dodajemy kilka dodatkowych argumentów do wywołania plot ().
pierwszy argument w naszej funkcji plot (), score ~ STR, jest ponownie formułą, która określa zmienne na osi y i X. Tym razem jednak dwie zmienne nie są zapisywane w oddzielnych wektorach, lecz są kolumnami CASchools. Dlatego R nie znajdzie ich bez poprawnego podania danych argumentu. dane muszą być zgodne z nazwą danych.ramka, do której należą zmienne, w tym przypadku CASchools. Kolejne argumenty są używane do zmiany wyglądu wykresu: podczas gdy main dodaje tytuł, xlab i ylab dodają własne etykiety do obu osi.
plot(score ~ STR, data = CASchools, main = "Scatterplot of TestScore and STR", xlab = "STR (X)", ylab = "Test Score (Y)")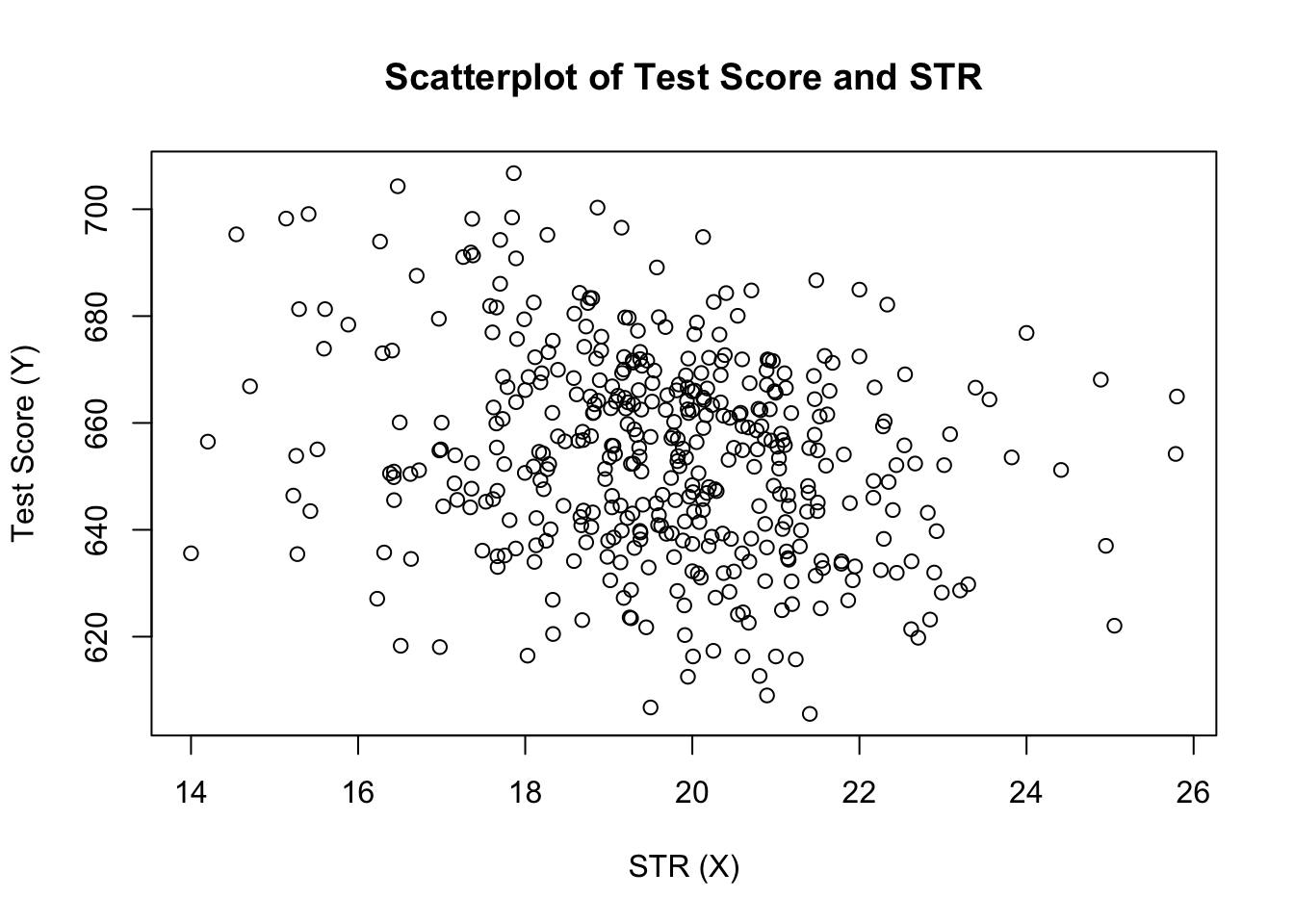
Wykres (rysunek 4.2 w książce) pokazuje rozrzut wszystkich obserwacji na temat stosunku uczeń-nauczyciel i wynik testu. Widzimy, że punkty są silnie rozproszone, a zmienne są ujemnie skorelowane. Oznacza to, że spodziewamy się niższych wyników testów w większych klasach.
funkcja cor () (zobacz ?cor for further info) może być użyty do obliczenia korelacji między dwoma wektorami liczbowymi.
cor(CASchools$STR, CASchools$score)#> -0.2263627jak już sugeruje punkt rozrzutu, korelacja jest ujemna, ale raczej słaba.
zadaniem, przed którym teraz stoimy, jest znalezienie linii, która najlepiej pasuje do danych. Oczywiście możemy po prostu trzymać się kontroli graficznej i analizy korelacji, a następnie wybrać najlepszą linię dopasowania, rzucając okiem. Byłoby to jednak raczej subiektywne: różni obserwatorzy rysowaliby różne linie regresji. W związku z tym interesują nas techniki, które są mniej arbitralne. Taką technikę daje zwykłe oszacowanie najmniejszych kwadratów (OLS).
zwykły Estymator najmniejszych kwadratów
Estymator OLS wybiera współczynniki regresji, tak aby szacowana linia regresji była jak najbardziej „bliska” obserwowanym punktom danych. Tutaj bliskość jest mierzona sumą kwadratowych błędów popełnionych w przewidywaniu \(Y\) podanym \(X\). Niech \(b_0\) i \(b_1\) będą niektórymi estymatorami \(\beta_0\) i \(\beta_1\). Wtedy suma błędów estymacji kwadratowej może być wyrażona jako
\
Estymator OLS w prostym modelu regresji jest parą estymatorów dla punktu przecięcia i nachylenia, co minimalizuje powyższe wyrażenie. Wyprowadzenie estymatorów OLS dla obu parametrów przedstawiono w dodatku 4.1 książki. Wyniki podsumowano w kluczowym koncepcie 4.2.
Estymator OLS, przewidywane wartości i pozostałości
estymatory OLS nachylenia \(\beta_1\) i przechwytywania \(\beta_0\) w prostym modelu regresji liniowej są\wartości przewidywane OLS \(\widehat{y}_i\) i pozostałości \(\hat{u}_i\) są\
szacowane przechwytywanie \(\Hat{\beta}_0\), parametr nachylenia \(\hat{\beta}_1\) i pozostałości \(\Left(\hat{u}_i\right)\) są obliczane z próbki \(N\) obserwacji \(x_i\) i \(y_i\), \(i\), \(…\), \(n\). Są to szacunki nieznanej populacji intercept \(\left (\beta_0 \right)\), slope \(\left(\beta_1\right)\) i error term \((u_i)\).
wzory przedstawione powyżej mogą na pierwszy rzut oka nie być zbyt intuicyjne. Poniższa interaktywna aplikacja ma pomóc ci zrozumieć mechanikę OLS. Możesz dodać obserwacje, klikając w układ współrzędnych, w którym dane są reprezentowane przez punkty. Gdy dostępne są dwie lub więcej obserwacji, aplikacja oblicza linię regresji za pomocą OLS i niektórych statystyk, które są wyświetlane w prawym panelu. Wyniki są aktualizowane w miarę dodawania kolejnych obserwacji do lewego panelu. Dwukrotne kliknięcie resetuje aplikację, tzn. wszystkie dane są usuwane.
istnieje wiele możliwych sposobów obliczania \(\Hat{\beta}_0\) i \(\hat{\beta}_1\) w R. na przykład, możemy zaimplementować formuły przedstawione w koncepcji klucza 4.2 z dwiema najbardziej podstawowymi funkcjami R: mean() I sum(). Zanim to zrobimy, dołączamy zestaw danych CASchools.
attach(CASchools) # allows to use the variables contained in CASchools directly# compute beta_1_hatbeta_1 <- sum((STR - mean(STR)) * (score - mean(score))) / sum((STR - mean(STR))^2)# compute beta_0_hatbeta_0 <- mean(score) - beta_1 * mean(STR)# print the results to the consolebeta_1#> -2.279808beta_0#> 698.9329wywołanie attached (CASchools) umożliwia nam adresowanie zmiennej zawartej w CASchools po jej nazwie: nie jest już konieczne używanie operatora $ w połączeniu z dataset: R może obliczyć nazwę zmiennej bezpośrednio.
R wykorzystuje obiekt w środowisku użytkownika, jeżeli obiekt ten posiada nazwę zmiennej zawartej w dołączonej bazie danych. Jednak lepiej jest zawsze używać charakterystycznych nazw, aby uniknąć takich (pozornie) ambiwalencji!
zauważ, że zmienne zawarte w dołączonym dataset CASchools adresujemy bezpośrednio do reszty tego rozdziału!
oczywiście istnieje jeszcze więcej ręcznych sposobów wykonywania tych zadań. Ponieważ OLS jest jedną z najczęściej używanych technik estymacji, R oczywiście zawiera już wbudowaną funkcję o nazwie lm () (model liniowy), która może być wykorzystana do przeprowadzenia analizy regresji.
pierwszym argumentem funkcji, która ma być określona, jest wzór regresji z podstawową składnią y ~ x, gdzie y jest zmienną zależną, a X zmienną objaśniającą. Argument data określa zestaw danych, który ma być użyty w regresji. Teraz wracamy do przykładu z książki, w którym analizuje się związek między wynikami testu a rozmiarami klas. Poniższy kod wykorzystuje lm () do replikacji wyników przedstawionych na rysunku 4.3 książki.
# estimate the model and assign the result to linear_modellinear_model <- lm(score ~ STR, data = CASchools)# print the standard output of the estimated lm object to the console linear_model#> #> Call:#> lm(formula = score ~ STR, data = CASchools)#> #> Coefficients:#> (Intercept) STR #> 698.93 -2.28dodajmy szacowaną linię regresji do wykresu. Tym razem również powiększamy zakresy obu osi ustawiając argumenty xlim i ylim.
# plot the dataplot(score ~ STR, data = CASchools, main = "Scatterplot of TestScore and STR", xlab = "STR (X)", ylab = "Test Score (Y)", xlim = c(10, 30), ylim = c(600, 720))# add the regression lineabline(linear_model) 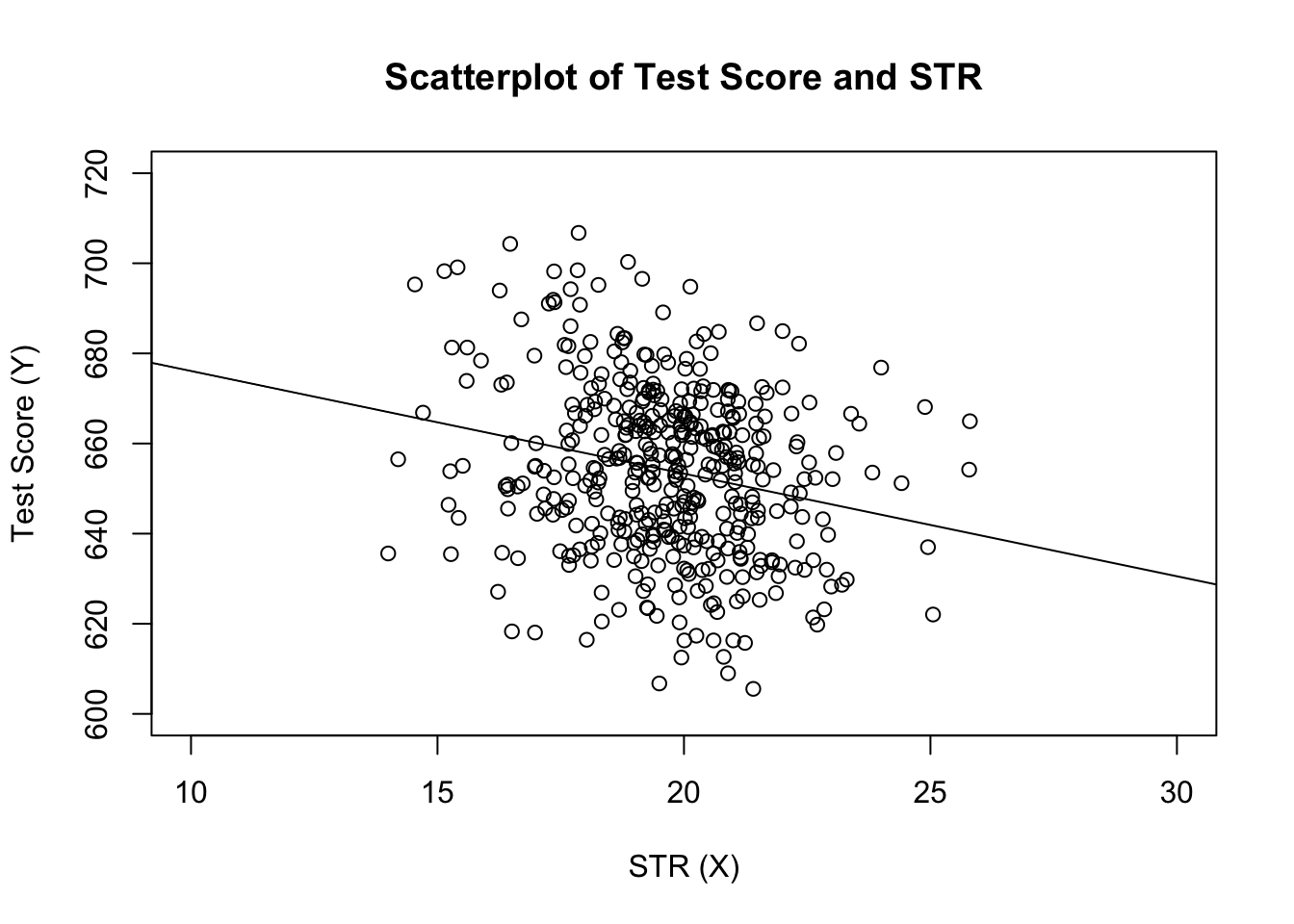
zauważyłeś, że tym razem nie przekazaliśmy parametrów przechwytywania i nachylenia do ably? Jeśli wywołasz abline () na obiekcie klasy lm, który zawiera tylko jeden regresor, R automatycznie rysuje linię regresji!