Terminologia:
- IDS = current from drain to source lub drain-Source current
- VDS = drain to source voltage
- L = length of the channel
teraz dla idealnego przypadku, w obszarze nasycenia, IDS staje się niezależne od VDS, tzn. w obszarze nasycenia kanał jest odcięty na końcu odpływu, a dalsze zwiększenie VDS nie ma wpływu na kształt kanału.
ale w praktyce wzrost VDS wpływa na kanał. W obszarze nasycenia, gdy VDS wzrasta, punkt zaciskania kanału jest przesunięty nieco od drenu, w kierunku źródła, gdy pole elektronowe drenu „odpycha” go z powrotem. Region zmniejszania odchylenia wstecznego rozszerza się, a efektywna długość kanału zmniejsza się o ∆l dla wzrostu VDS.
w ten sposób kanał nie „dotyka” odpływu i nabiera asymetrycznego kształtu, który jest cieńszy na końcu odpływu. Zjawisko to znane jest jako modulacja długości kanału.
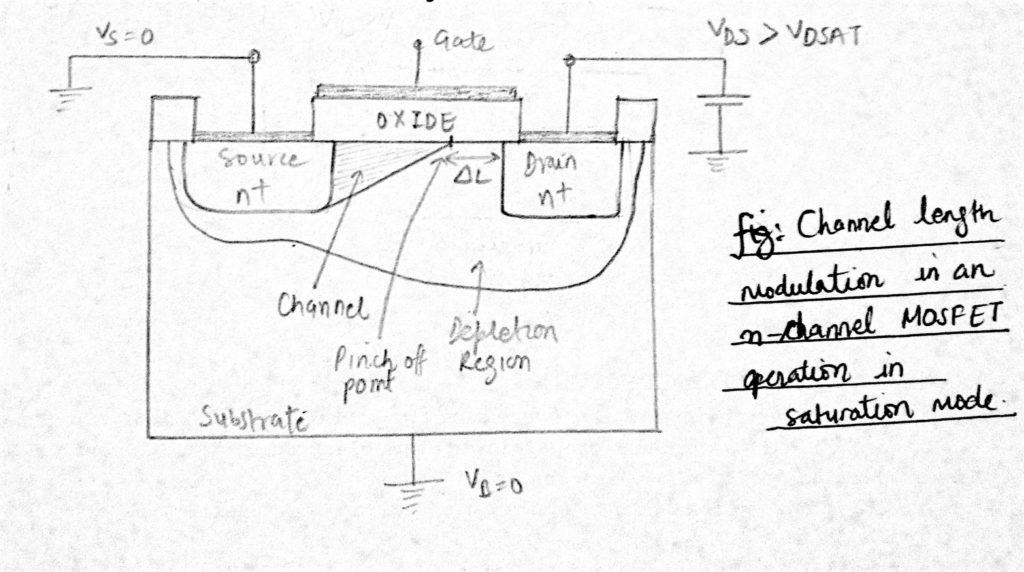
W dużych urządzeniach efekt ten jest znikomy, ale dla urządzeń krótszych ∆L/L staje się ważne. Również w obszarze nasycenia ze względu na modulację długości kanału, IDS wzrasta wraz ze wzrostem VDS, a także wzrasta wraz ze spadkiem długości kanału L.
krzywa napięcie-prąd nie jest już płaska w tym regionie.
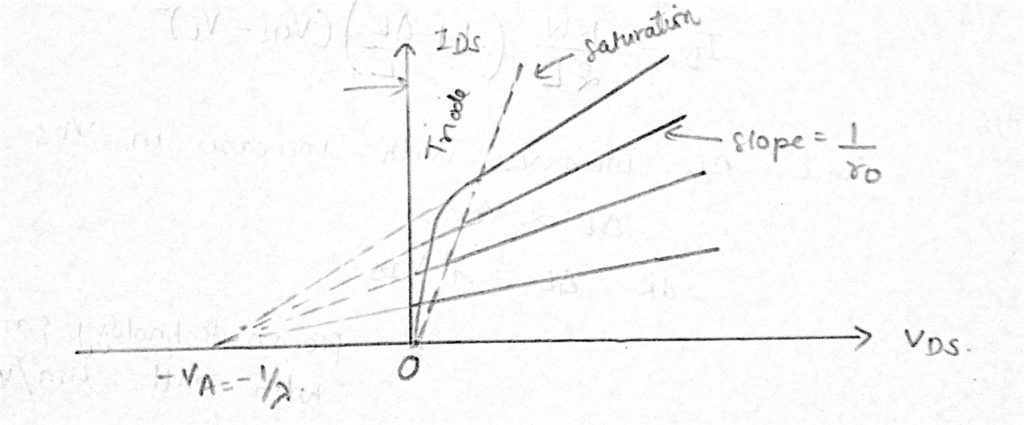
prąd spustowy z modulacją długości kanału jest podawany przez:
DERYWACJA:
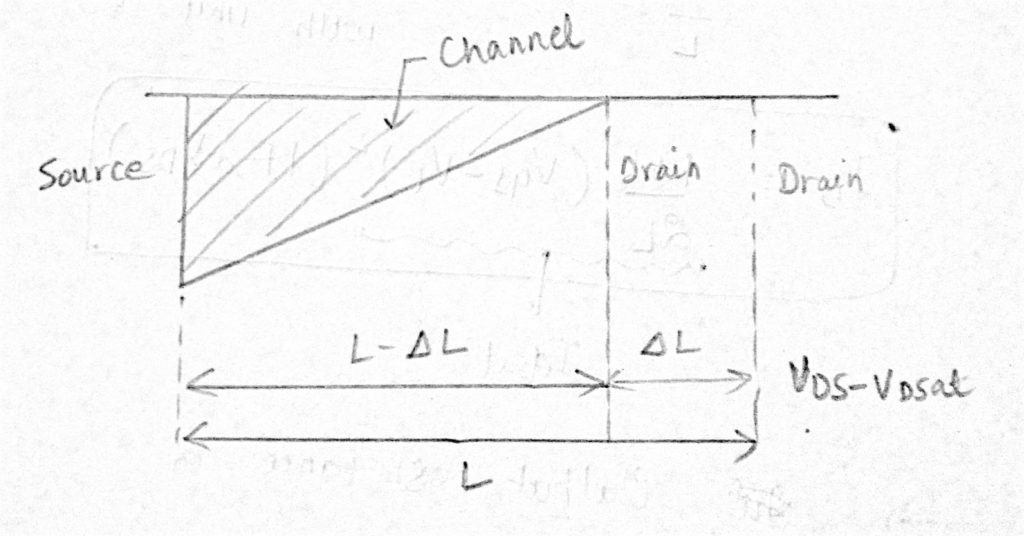
aby uwzględnić zależność ID od VDS w obszarze nasycenia, zastąp L przez L – ∆L. wiemy, że w obszarze nasycenia drenaż do prądu źródłowego (IDS = ID) jest podany przez:
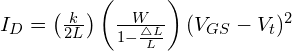
zakładając 
ponieważ ∆l wzrasta wraz ze wzrostem VDS
lub
gdzie, 
= parametr technologii procesu z jednostką µm / V.
dlatego,
gdzie,
= parametr technologii procesu z jednostką V-1
