oto przewodnik krok po kroku, jak uruchomić analizę klastra k-means na arkuszu kalkulacyjnym Excela od początku do końca. Należy pamiętać, że istnieje szablon Excel, który automatycznie uruchamia analizę klastra, dostępny do bezpłatnego pobrania na tej stronie internetowej. Ale jeśli chcesz wiedzieć, jak samemu uruchomić klastrowanie k-means w programie Excel, ten artykuł jest dla ciebie.
oprócz tego artykułu mam również wideo pokazujące, jak uruchomić analizę klastra w programie Excel.
- Krok pierwszy-zacznij od zestawu danych
- Krok drugi – jeśli tylko dwie zmienne, użyj wykresu punktowego w programie Excel
- Krok trzeci-Oblicz odległość od każdego punktu danych do środka klastra
- jak działa kalkulacja?
- Krok czwarty-Oblicz średnią (średnią) każdego zestawu klastrów
- krok piąty-powtórz Krok 3-Odległość od poprawionej średniej
- ostatni krok-wykres i podsumowanie klastrów
Krok pierwszy-zacznij od zestawu danych
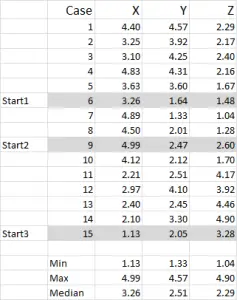
Rysunek 1
w tym przykładzie używam 15 przypadków (lub respondentów), gdzie mamy dane dla trzech zmiennych-ogólnie oznaczonych X, Y i Z.
należy zauważyć, że dane są skalowane 1-5 w tym przykładzie. Twoje dane mogą być w dowolnej formie, z wyjątkiem nominalnej skali danych (zobacz artykuł, jakich danych użyć).
Uwaga: wolę używać skalowanych danych-ale nie jest to obowiązkowe. Powodem tego jest „zawierać” wszelkie wartości odstające. Powiedzmy, na przykład, używam danych o dochodach (miara demograficzna) – większość danych może wynosić około $40,000 do $100,000, ale mam jedną osobę z dochodem w wysokości $5m. łatwiej jest mi zaklasyfikować tę osobę w przedziale dochodów „ponad $250,000” i skalować dochód 1-9-ale to zależy od Ciebie, w zależności od danych, z którymi pracujesz.
z tego przykładowego zestawu widać, że wyróżniono trzy pozycje startowe – omówimy je w kroku trzecim poniżej.
Krok drugi – jeśli tylko dwie zmienne, użyj wykresu punktowego w programie Excel
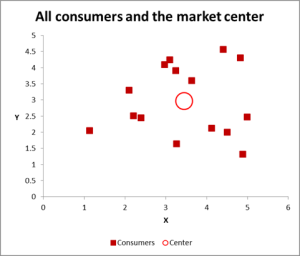
Rysunek 2
w tym przykładzie analizy klastra używamy trzech zmiennych – ale jeśli masz tylko dwie zmienne do klastra, to wykres punktowy jest doskonałym sposobem na rozpoczęcie. Czasami można gromadzić dane za pomocą środków wizualnych.
jak widać na tym wykresie punktowym, każdy pojedynczy przypadek (co nazywam konsumentem w tym przykładzie) został zmapowany, wraz ze średnią (średnią) dla wszystkich przypadków (czerwone kółko).
w zależności od sposobu wyświetlania danych / wykresu-wydaje się, że istnieje kilka klastrów. W tym przypadku można zidentyfikować trzy lub cztery stosunkowo różne klastry-jak pokazano na następnym wykresie.
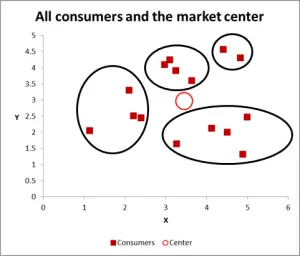
Rysunek 3
na następnym wykresie zidentyfikowałem prawdopodobny klaster i okrążyłem go. Jak już zasugerowałem, dobre podejście, gdy są tylko dwie zmienne do rozważenia – ale czy w tym przypadku mamy trzy zmienne (i możesz mieć więcej), więc to wizualne podejście będzie działać tylko dla podstawowych zestawów danych – więc teraz spójrzmy na to, jak wykonać obliczenia Excela dla K-oznacza grupowanie.
Krok trzeci-Oblicz odległość od każdego punktu danych do środka klastra
w tym przykładzie Przyjmijmy, że chcemy zidentyfikować tylko trzy segmenty/klastry. Tak, istnieją cztery klastry widoczne na powyższym diagramie, ale to tylko patrzy na dwie ze zmiennych. Pamiętaj, że możesz użyć tego podejścia do Excela, aby zidentyfikować dowolną liczbę klastrów – po prostu postępuj zgodnie z tą samą koncepcją, jak wyjaśniono poniżej.
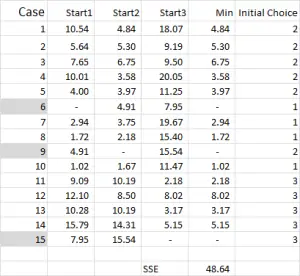
Rysunek 4
w przypadku grupowania k-means zazwyczaj wybieramy kilka przypadkowych przypadków (punkty wyjściowe lub nasiona), aby rozpocząć analizę.
w tym przykładzie-ponieważ chcę utworzyć trzy klastry, będę potrzebował trzech punktów początkowych. Dla tych punktów startowych wybrałem przypadki 6, 9 i 15 – ale dowolne losowe punkty mogą być również odpowiednie.
wybrałem te przypadki, ponieważ-patrząc tylko na zmienną X-przypadek 6 był medianą, przypadek 9 był maksimum, a przypadek 15 był minimum. Sugeruje to, że te trzy przypadki są nieco różne od siebie, więc dobre punkty wyjścia, ponieważ są one rozłożone.
proszę odnieść się do artykułu na temat dlaczego analiza klastra czasami generuje różne wyniki.
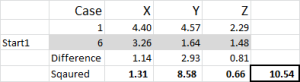
odnosząc się do wyniku tabeli-jest to nasze pierwsze obliczenie w Excelu i generuje nasz „początkowy wybór” klastrów. Start 1 to dane dla przypadku 6, start 2 to przypadek 9, a start 3 to przypadek 15. Należy pamiętać, że przecięcie każdego z nich daje 0 ( – ) w tabeli.
jak działa kalkulacja?
5
spójrzmy na pierwszą liczbę w tabeli-przypadek 1, start 1 = 10.54.
pamiętaj, że arbitralnie wyznaczyliśmy przypadek 6 jako nasz losowy punkt startowy dla klastra 1. Chcemy obliczyć odległość i używamy metody sumy kwadratów – jak pokazano tutaj. Obliczamy różnicę między każdym z trzech punktów danych w zbiorze, a następnie do kwadratu różnice, a następnie sumujemy je.
możemy to zrobić „mechanicznie”, jak pokazano tutaj – ale Excel ma wbudowaną formułę do użycia: SUMXMY2-jest to znacznie bardziej wydajne w użyciu.
Wracając do rysunku 4, znajdujemy minimalną odległość dla każdego przypadku od każdego z trzech punktów początkowych-to mówi nam, do którego klastra (1, 2 lub 3) jest najbliższy przypadek – co jest pokazane w „initial choice column”.
Krok czwarty-Oblicz średnią (średnią) każdego zestawu klastrów
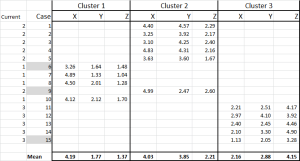
Rysunek 6
teraz przydzieliliśmy każdy przypadek do jego początkowego klastra – i możemy to rozłożyć za pomocą instrukcji IF w tabeli (jak pokazano na rysunku 6).
na dole tabeli mamy średnią (średnią) każdego z tych przypadków. N0w – zamiast polegać tylko na jednym „reprezentatywnym” punkcie danych-mamy zestaw przypadków reprezentujących każdy.
krok piąty-powtórz Krok 3-Odległość od poprawionej średniej
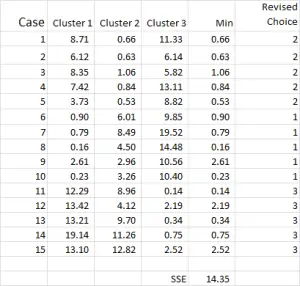
Rysunek 7
proces analizy klastra staje się teraz kwestią powtarzania kroków 4 i 5 (iteracji), aż klastry się ustabilizują.
za każdym razem używamy poprawionej średniej dla każdego klastra. Dlatego Rysunek 7 pokazuje naszą drugą iterację-ale tym razem używamy środków wygenerowanych na dole rysunku 6 (zamiast punktów początkowych z rysunku 1).
teraz widać, że nastąpiła niewielka zmiana w aplikacji klastra, a przypadek 9-jeden z naszych punktów wyjściowych-został ponownie przydzielony.
możesz również zobaczyć sumę błędu kwadratowego (SSE) obliczoną na dole – która jest sumą każdej z minimalnych odległości. Naszym celem jest teraz powtarzanie kroków 4 i 5, dopóki SSE nie wykaże minimalnej poprawy i/lub zmiany alokacji klastrów będą niewielkie w każdej iteracji.
ostatni krok-wykres i podsumowanie klastrów
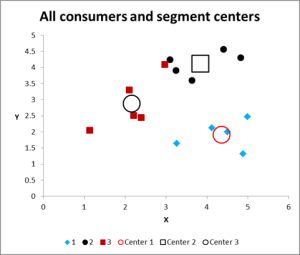
Rysunek 8
po uruchomieniu wielu iteracji mamy teraz wyjście do wykresu i podsumowania danych.
oto wykres wyjściowy dla tego przykładowego Excela analizy klastra.
jak widać, pokazano trzy różne gromady, wraz z centroidami (średnią) każdego z nich-większymi symbolami.
możemy również przedstawić te dane w formie tabeli, jeśli jest to wymagane, ponieważ opracowaliśmy je w Excelu.
Proszę spojrzeć na przypadek w klastrze 3-mały czerwony kwadrat tuż obok czarnej kropki w górnej środkowej części wykresu. Ten przypadek znajduje się tam z powodu wpływu trzeciej zmiennej, która nie jest pokazana na tym wykresie dwóch zmiennych.