zakładana wiedza
uczniowie będą mieli szerokie nieformalne doświadczenie z geometrią we wcześniejszych latach, co zapewni dobrą intuicyjną podstawę do bardziej systematycznego podejścia do geometrii odpowiedniego w latach 7-10. Poszczególne tematy z Lat F-6 związane z tym modułem to:
- zastosowanie kompasów i linijek oraz staranne rysowanie figur geometrycznych.
- rodzaje kątów, w tym co najmniej kąty proste, kąty ostre, kąty rozwarte i
kąty odruchowe. - Trójkąty, w tym nieformalne wprowadzenie do trójkątów równoramiennych i równobocznych.
- kwadraty, w tym nieformalne wprowadzenie do kwadratów, prostokątów, równoległoboków, trapezów i rombów.
- nieformalne doświadczenie z tłumaczeniami, refleksjami, obrotami i powiększeniami,
i z symetrią w kontekście działań takich jak składanie trójkąta równoramiennego, prostokąta lub rombu.
Motywacja
 Geometria służy do modelowania otaczającego nas świata. Widok dachów domów ujawnia trójkąty, trapezy i prostokąty, natomiast wzory płytek na chodnikach i łazienkach wykorzystują sześciokąty, pięciokąty, trójkąty i kwadraty.
Geometria służy do modelowania otaczającego nas świata. Widok dachów domów ujawnia trójkąty, trapezy i prostokąty, natomiast wzory płytek na chodnikach i łazienkach wykorzystują sześciokąty, pięciokąty, trójkąty i kwadraty.
Budowniczowie, kafelkarze, architekci, graficy i projektanci stron internetowych rutynowo wykorzystują pomysły geometryczne w swojej pracy. Klasyfikacja takich obiektów geometrycznych i badanie ich właściwości są bardzo ważne. Geometria ma również wiele zastosowań w sztuce.
tak jak arytmetyka ma liczby jako podstawowe obiekty badań, tak punkty, linie i okręgi są podstawowym budulcem geometrii płaszczyzny.
w geometrii szkoły średniej zaczynamy od kilku intuicyjnych pomysłów (punktów, linii i kątów), które wcale nie są łatwe do precyzyjnego zdefiniowania, a następnie kilka definicji (pionowo przeciwległe kąty, równoległe linie itp.) i z nich wyciągamy ważne fakty, które często nazywane są twierdzeniami. W szkole średniej poziom rygoru powinien rozwijać się powoli z roku na rok, ale na każdym etapie jasne wyznaczanie jest bardzo ważne i należy podkreślić.
w ten sposób geometria daje uczniom możliwość rozwijania swojej intuicji geometrycznej, która ma zastosowanie w wielu dziedzinach życia, a także nauczenia się konstruowania logicznych argumentów i dokonywania dedukcji w otoczeniu, które jest w większości niezależne od liczby
.
zawartość
punkty i linie
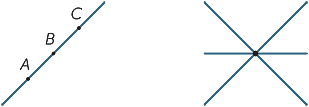
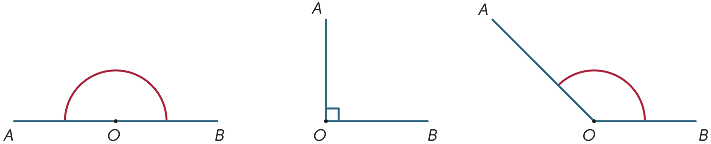
najprostszymi obiektami w geometrii płaszczyzny są punkty i linie. Ponieważ są one tak proste, trudno jest je precyzyjnie zdefiniować, więc zamiast tego staramy się dać uczniom przybliżony opis ich właściwości, który jest zgodny z naszą intuicją. Punkt oznacza pozycję, ale nie ma rozmiaru. W praktyce, gdy rysujemy punkt, ma on wyraźnie określoną szerokość, ale reprezentuje punkt w naszej wyobraźni. Linia nie ma szerokości i rozciąga się w nieskończoność w obu kierunkach. Kiedy rysujemy linię, ma ona szerokość i ma końce, więc tak naprawdę nie jest to linia, ale reprezentuje linię w naszej wyobraźni. Biorąc pod uwagę dwa różne punkty A i B, istnieje jedna (i tylko jedna) linia, która przechodzi przez oba punkty. Używamy wielkich liter, aby odnieść się do punktów i linii nazw, albo podając dwa punkty na linii, albo używając małych liter, takich jak  I m. Tak więc, dana linia poniżej jest określana jako linia AB lub jako linia
I m. Tak więc, dana linia poniżej jest określana jako linia AB lub jako linia  .
.

biorąc pod uwagę dwie różne linie, istnieją dwie możliwości: mogą się spotkać w jednym punkcie lub nigdy się nie spotkać, bez względu na to, jak daleko są rozciągnięte (lub wyprodukowane). Linie, które nigdy się nie spotykają, nazywane są równoległymi. Na drugim diagramie zapisujemy AB / / CD.
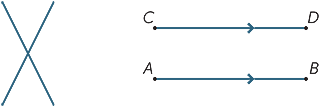
trzy (lub więcej) punkty leżące na linii prostej nazywane są kolinearnymi.
trzy (lub więcej) linie, które spotykają się w jednym punkcie, są nazywane jednocześnie.
|
|
|
Ćwiczenie 1
narysuj trzy linie, które nie są równoległe, tak aby żadne dwie nie były równoległe.
Ćwiczenie 2
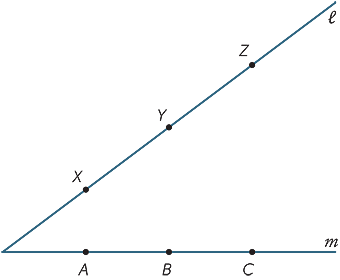
zrób dużą kopię poniższego diagramu. Punkty X, Y, Z są dowolnymi punktami na linii  i A, B, C są dowolnymi punktami na linii m. Dołącz AY i XB nazywają swoje skrzyżowanie R. Dołącz BZ i YC i nazwij ich skrzyżowanie P. Dołącz CX i ZA i nazwij ich skrzyżowanie Q. co zauważysz o punktach P, Q, R? (Wynik ten nazywany jest twierdzeniem Pappusa, c. 340 AD.)
i A, B, C są dowolnymi punktami na linii m. Dołącz AY i XB nazywają swoje skrzyżowanie R. Dołącz BZ i YC i nazwij ich skrzyżowanie P. Dołącz CX i ZA i nazwij ich skrzyżowanie Q. co zauważysz o punktach P, Q, R? (Wynik ten nazywany jest twierdzeniem Pappusa, c. 340 AD.)
odstępy, promienie i kąty
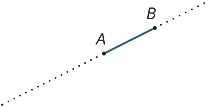 Załóżmy, że A i B są dwoma punktami na linii. Odstęp
Załóżmy, że A i B są dwoma punktami na linii. Odstęp
AB jest częścią linii między A i B, w tym dwoma punktami końcowymi.
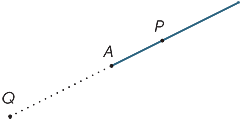 punkt A na diagramie dzieli linię na dwie części zwane promieniami. Promień AP jest tym promieniem, który zawiera punkt P (i punkt A).
punkt A na diagramie dzieli linię na dwie części zwane promieniami. Promień AP jest tym promieniem, który zawiera punkt P (i punkt A).
Kąty
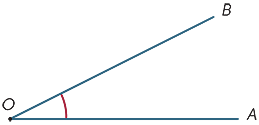
 na diagramie obszar zacieniony między promieniami OA i OB nazywany jest kątem AOB lub kątem BOA. Znak kąta
na diagramie obszar zacieniony między promieniami OA i OB nazywany jest kątem AOB lub kątem BOA. Znak kąta ![]() jest zapisany, więc piszemy
jest zapisany, więc piszemy ![]() AOB.
AOB.
 zacieniony obszar na zewnątrz nazywany jest kątem refleksyjnym utworzonym przez OA i OB. W większości przypadków, o ile nie określimy słowa odruch, wszystkie nasze kąty odnoszą się do obszaru między promieniami, a nie poza nimi.
zacieniony obszar na zewnątrz nazywany jest kątem refleksyjnym utworzonym przez OA i OB. W większości przypadków, o ile nie określimy słowa odruch, wszystkie nasze kąty odnoszą się do obszaru między promieniami, a nie poza nimi.
Rozmiar kąta
 wyobraź sobie, że promień OB jest obracany wokół punktu O, aż leży wzdłuż OA. Wielkość skrętu nazywa się wielkością kąta AOB. Podobnie możemy zdefiniować wielkość kąta refleksyjnego.
wyobraź sobie, że promień OB jest obracany wokół punktu O, aż leży wzdłuż OA. Wielkość skrętu nazywa się wielkością kąta AOB. Podobnie możemy zdefiniować wielkość kąta refleksyjnego.
często używamy małych liter greckich, α, β, γ,… do reprezentowania wielkości kąta.
wielkość kąta odpowiadająca jednemu pełnemu obrotowi została podzielona (przez Babilończyków)na 360 równych części, które nazywamy stopniami. (Prawdopodobnie wybrali 360, ponieważ było blisko liczby dni w roku.) Stąd wielkość kąta prostego wynosi 180° , a wielkość kąta prostego 90°. Inne kąty można zmierzyć (w przybliżeniu) za pomocą kątomierza.
|
|
||
| kąt prosty | kąt prosty |
kąt rozwarty |
kąty są klasyfikowane według ich wielkości. Mówimy, że kąt o rozmiarze α jest ostry
(słowo oznaczające „ostry”), jeśli 0° < α < 90°, α jest rozwarty (słowo oznaczające „tępy”), jeśli
90° < α < 180°, a α jest refleksyjny, jeśli 180° < α < 360°.
ponieważ kątomierz ma dwie skale, uczniowie muszą być ostrożni podczas rysowania i
mierzyć kąty. Warto ćwiczyć, aby użyć kątomierza do narysowania niektórych kątów, takich jak 30°, 78°, 130°, 163°.
3
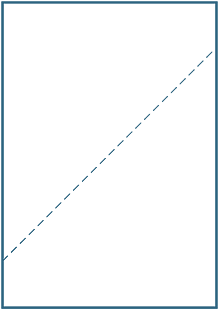 złóż arkusz papieru A4 pasujący do (po przekątnej) przeciwległych narożników. Narysuj linię wzdłuż tworzonego zagniecenia i zmierz kąty między zagnieceniem a bokiem.
złóż arkusz papieru A4 pasujący do (po przekątnej) przeciwległych narożników. Narysuj linię wzdłuż tworzonego zagniecenia i zmierz kąty między zagnieceniem a bokiem.
w powyższym ćwiczeniu oba kąty tworzą razem linię prostą, a więc dodają się do 180°. Dwa kąty, które dodają do 180°, nazywane są kątami dodatkowymi; tak więc 45° i 135° są kątami dodatkowymi.
Dwa kąty, które dodają do 90°, nazywane są komplementarnymi; zatem 23° i 67° to
kąty komplementarne.
kąty w punkcie
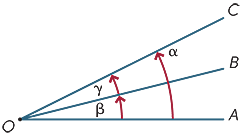 mówi się, że dwa kąty w punkcie sąsiadują, jeśli mają wspólny promień. Stąd na diagramie sąsiadują ze sobą
mówi się, że dwa kąty w punkcie sąsiadują, jeśli mają wspólny promień. Stąd na diagramie sąsiadują ze sobą ![]() AOB i
AOB i ![]() BOC.
BOC.
można dodać Kąty przyległe, więc na schemacie
α = β + γ.
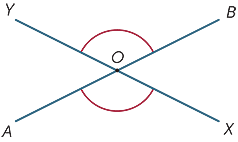
gdy dwie linie przecinają się, w punkcie przecięcia powstają cztery kąty.
na diagramie kąty oznaczone ![]() AOX i
AOX i ![]() BOY nazywane są pionowo przeciwległymi.
BOY nazywane są pionowo przeciwległymi.
 od
od
-
 AOX jest uzupełnieniem pudełka
AOX jest uzupełnieniem pudełka  (kąt prosty).
(kąt prosty). -
 BOY jest również uzupełnieniem
BOY jest również uzupełnieniem  pudełka (kąt prosty),
pudełka (kąt prosty),
możemy wywnioskować, że te pionowo przeciwległe kąty,
![]() AOX i
AOX i ![]() BOY są równe. Mamy więc nasze pierwsze
BOY są równe. Mamy więc nasze pierwsze
ważne twierdzenie geometryczne:
kąty przeciwległe w pionie są równe.
wynik w geometrii (i ogólnie w matematyce) jest często nazywany twierdzeniem. Twierdzenie jest ważnym stwierdzeniem, które można udowodnić za pomocą dedukcji logicznej. Powyższy argument jest dowodem twierdzenia; czasami dowody są przedstawiane formalnie po stwierdzeniu twierdzenia.
 Jeśli dwie linie przecinają się tak, że wszystkie cztery kąty są prostopadłe, to linie są prostopadłe.
Jeśli dwie linie przecinają się tak, że wszystkie cztery kąty są prostopadłe, to linie są prostopadłe.
kąty w punkcie-argumenty geometryczne
w argumentach geometrycznych można użyć następujących powodów:
- Kąty przyległe mogą być dodawane lub odejmowane.
- kąty w rewolucji dodać do 360°.
- kąty w linii prostej do 180°.
- kąty przeciwległe pionowo są równe.
linie poprzeczne i równoległe
 poprzeczna jest linią, która spełnia dwie inne linie.
poprzeczna jest linią, która spełnia dwie inne linie.
odpowiednie kąty
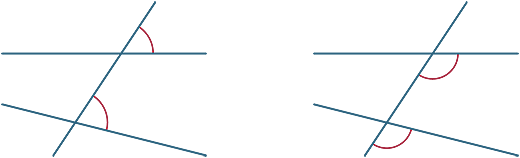
różne kąty są tworzone przez poprzeczne. Na poniższych diagramach dwa zaznaczone kąty nazywane są odpowiednimi kątami.
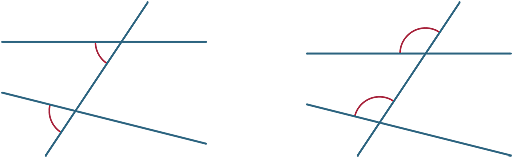
 przyjrzymy się teraz, co się dzieje, gdy dwie linie przecięte przez poprzeczkę są równoległe.
przyjrzymy się teraz, co się dzieje, gdy dwie linie przecięte przez poprzeczkę są równoległe.
Inituitely, jeśli kąt α był większy niż β, to CD przekroczyłoby AB na lewo od F, a jeśli byłoby mniejsze niż β, to skrzyżowałoby się na prawo od F. ponieważ linie w ogóle się nie krzyżują, α nie może być ani mniejszy, ani większy niż β, a więc równa się β.
alternatywnie, wyobraźmy sobie tłumaczenie kąta QGD wzdłuż GF, aż G zbiega się z F. ponieważ linie są równoległe, spodziewamy się, że kąt α zbiega się z kątem β. Ta obserwacja prowadzi nas do przypuszczeń, że:
odpowiednie kąty utworzone z równoległych linii są równe.
nie możemy udowodnić tego wyniku, chociaż wykazaliśmy, że jest on geometrycznie prawdopodobny. Przyjmiemy to jako aksjomat geometrii. Aksjomat jest stwierdzeniem, którego nie możemy udowodnić, ale które jest intuicyjnie rozsądne. Zauważ, że wiele faktów, które już ustaliliśmy, takich jak: kąty przyległe mogą być dodawane, a dwa punkty określają linię itp., są również aksjomatami, choć nie określiliśmy ich wyraźnie w ten sposób.
Kąty naprzemianległe
na każdym diagramie dwa zaznaczone kąty nazywane są kątami naprzemianległymi (ponieważ znajdują się na naprzemianległych bokach poprzecznej).

 jeśli linie AB i CD są równoległe, to alternatywne kąty są równe. Ten wynik można teraz udowodnić.
jeśli linie AB i CD są równoległe, to alternatywne kąty są równe. Ten wynik można teraz udowodnić.
![]() DGQ = α (odpowiednie kąty, AB / / CD)
DGQ = α (odpowiednie kąty, AB / / CD)
![]() DGQ = β (pionowo przeciwległe kąty w G)
DGQ = β (pionowo przeciwległe kąty w G)
więc α = β.
podsumowując:
alternatywne Kąty utworzone z równoległych linii są równe.
Kąty Współwewnętrzne
wreszcie, na każdym diagramie poniżej, dwa oznaczone kąty są nazywane kątami współwewnętrznymi i leżą po tej samej stronie poprzecznej.

jeśli linie AB i CD są równoległe, to oczywiste jest, że kąty współ-wewnętrzne nie są równe, ale okazuje się, że są uzupełniające, czyli ich suma wynosi 180°.
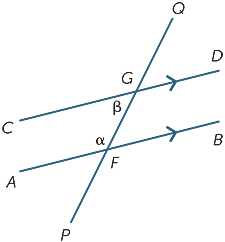 jest to wynik, który jest również łatwy do udowodnienia:
jest to wynik, który jest również łatwy do udowodnienia:
![]() BFG = β (kąty alternatywne, AB ||CD)
BFG = β (kąty alternatywne, AB ||CD)
α + β = 180° (kąt prosty przy F)
podsumowując:
Kąty Współwewnętrzne utworzone z równoległych linii są uzupełniające.
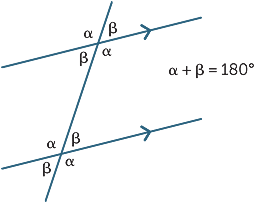 trzy wyniki można podsumować
trzy wyniki można podsumować
za pomocą następującego diagramu:
przykłady liczbowe
podane informacje o kątach na diagramie, możemy użyć powyższych wyników, aby znaleźć Rozmiar innych kątów na diagramie. Jest to prosta, ale bardzo ważna umiejętność, często określana nieformalnie jako ANGLE chasing. W rozwiązywaniu problemów kolejność kroków nie zawsze jest wyjątkowa. Może być kilka różnych, ale równie ważnych podejść.
na przykład na poniższym diagramie szukamy wielkości kąta BAC.

![]() DCA = 102° (kąty naprzemienne, AC / BD)
DCA = 102° (kąty naprzemienne, AC / BD)
![]() BAC = 78° (kąty współwłasności, AB / / CD)
BAC = 78° (kąty współwłasności, AB / / CD)
ćwiczenie 4
użyj naprzemiennej sekwencji kroków, aby znaleźć ![]() BAC.
BAC.
Ćwiczenia 5
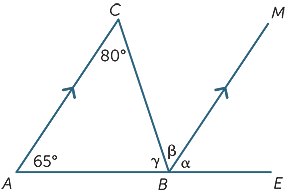 używając tylko właściwości równoległych linii, Znajdź (z przyczynami) brakujące kąty na poniższym diagramie.
używając tylko właściwości równoległych linii, Znajdź (z przyczynami) brakujące kąty na poniższym diagramie.
ćwiczenie 6
znajdź wartość α na poniższym diagramie.
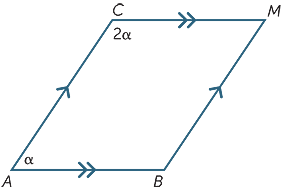
Converse twierdzenia
wiele twierdzeń w matematyce ma converse, w którym implikacja idzie w przeciwnym kierunku. Na przykład polecenie
’ każda liczba parzysta kończy się na 0, 2, 4, 6 lub 8.’
ma konwersję
’ każda liczba kończąca się na 0, 2, 4, 6 lub 8 jest parzysta.”
to konkretne stwierdzenie i jego konwersja są prawdziwe, ale nie zawsze jest to przypadek
.
na przykład, następujące dwa wyrażenia są konwersjami siebie:
'każda wielokrotność 4 jest liczbą parzystą.’
’ każda liczba parzysta jest wielokrotnością 4.”
i tu pierwsze stwierdzenie jest prawdziwe, ale drugie jest fałszywe.
ćwiczenie 7
Zapisz:
a![]() prawdziwe oświadczenie geometryczne, którego konwersja jest również prawdziwa,
prawdziwe oświadczenie geometryczne, którego konwersja jest również prawdziwa,
b![]() fałszywe oświadczenie geometryczne, którego konwersja jest prawdziwa,
fałszywe oświadczenie geometryczne, którego konwersja jest prawdziwa,
c![]() fałszywe oświadczenie geometryczne, którego konwersja jest również fałszywa.
fałszywe oświadczenie geometryczne, którego konwersja jest również fałszywa.
twierdzenie odwrotne dla linii równoległych
widzieliśmy, że odpowiadające im kąty utworzone z linii równoległych są równe. Możemy zapisać polecenie converse w następujący sposób.
stwierdzenie: jeśli linie są równoległe, to odpowiednie kąty są równe.
Converse: Jeśli odpowiednie kąty są równe, to linie są równoległe.
twierdzenie converse jest również prawdziwe i jest często używane do udowodnienia, że dwie linie są równoległe. To samo dotyczy kątów naprzemianległych i współ-wewnętrznych.
polecenie: jeśli linie są równoległe, to kąty alternatywne są równe.
Konwersja: jeśli alternatywne kąty są równe, to linie są równoległe.
stwierdzenie: jeśli linie są równoległe, to kąty współwewnętrzne są dodatnie.
Converse: Jeśli kąty współwewnętrzne są dodatnie, to linie są równoległe.
tak więc na każdym diagramie linie AB i CD są równoległe.

ćwiczenia 8
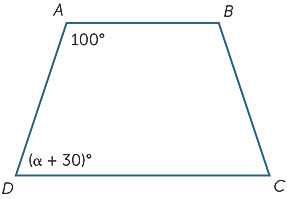 jaka wartość α spowoduje, że AB będzie równoległa do CD?
jaka wartość α spowoduje, że AB będzie równoległa do CD?
dowody trzech Konwersów
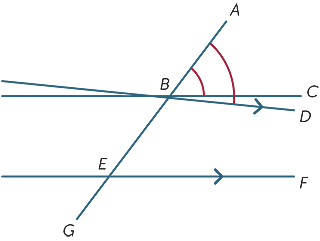 Zakładamy, że odpowiednie kąty utworzone przez poprzeczkę są równe i pokazujemy, że linie są równoległe.
Zakładamy, że odpowiednie kąty utworzone przez poprzeczkę są równe i pokazujemy, że linie są równoległe.
na diagramie Zakładamy, że ![]() ABC =
ABC = ![]() BEF.
BEF.
jeśli BC i EF nie są równoległe, narysuj
BD równolegle do EF.
teraz, ponieważ BD i EF są równoległe ![]() ABD =
ABD = ![]() BEF i tak
BEF i tak ![]() ABC =
ABC = ![]() ABD, co jest wyraźnie niemożliwe, chyba że linie BC i BD są takie same. Stąd linie BC i EF są równoległe.
ABD, co jest wyraźnie niemożliwe, chyba że linie BC i BD są takie same. Stąd linie BC i EF są równoległe.
Pozostałe dowody następują w ten sam sposób.
ćwiczenie 9
daj dowód drugiego twierdzenia converse (kąty alternatywne).
suma kątowa trójkąta
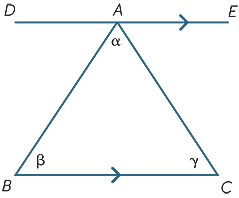 wyniki z poprzedniej sekcji można wykorzystać do wydedukowania jednego z najważniejszych faktów w geometrii-suma kątów trójkąta wynosi 180° .
wyniki z poprzedniej sekcji można wykorzystać do wydedukowania jednego z najważniejszych faktów w geometrii-suma kątów trójkąta wynosi 180° .
zaczynamy od trójkąta ABC z kątami α, β, γ, Jak pokazano. Narysuj linię dae równolegle do BC. Wtedy,
![]() DAB = β (kąty alternatywne, BC / / DE)
DAB = β (kąty alternatywne, BC / / DE)
![]() EAC = γ (kąty alternatywne, BC||DE)
EAC = γ (kąty alternatywne, BC||DE)
α+ β + γ = 180° (kąt prosty).
tak więc udowodniliśmy twierdzenie
suma kątów w trójkącie wynosi 180°.
czworokąt to płaszczyzna ograniczona czterema bokami.
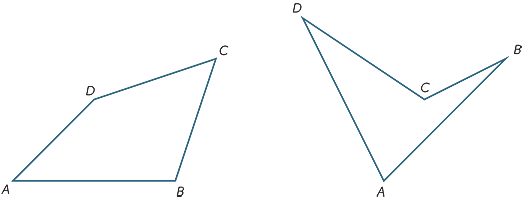
ćwiczenie 10
dzieląc czworokąt ABCD na dwa trójkąty, znajdź sumę kątów.
Links forward
materiał w tym module zaczął umieszczać geometrię na dość systematycznym fundamencie starannie zdefiniowanych obiektów, aksjomatów, które należy przyjąć, i twierdzeń, które udowodniliśmy. Na tej podstawie możemy opracować systematyczny rachunek geometrii płaszczyzny obejmujący:
- twierdzenie Pitagorasa
- Trójkąty przystające i przystające
- podobieństwo i podobne Trójkąty
- równoramienne i trójkąty równoboczne
- kwadraty specjalne, w tym kwadraty, prostokąty, równoległoboki, romby i trapezy
- geometria kół.
geometria płaszczyzny będzie również fundamentalna w wielu innych dziedzinach matematyki lat 7-10:
- przekształcenia
- geometria trójwymiarowa
- obszary i tomy
- Trygonometria
- geometria współrzędnych
- wykresy okręgów i paraboli.
idee stycznych i obszarów prowadzą z kolei do rachunku różniczkowego w latach 11-12.
Historia i zastosowanie
Historia
niesamowite konstrukcje piramid i ogromnych świątyń Egiptu pokazują, że Egipcjanie musieli mieć bardzo dobrą praktyczną wiedzę i zrozumienie podstawowej geometrii, przynajmniej na poziomie praktycznym. Z drugiej strony, nie ma dowodów na to, że usystematyzowali tę wiedzę w jakikolwiek sposób formalny. Pozostawiono to starożytnym Grekom. Nie mamy szczegółowej wiedzy na temat tej systematyzacji, z wyjątkiem twierdzenia, że Thales (ok. 624 p. n. e. – OK. 546 p. n. e.) podał pierwsze „dowody” faktów geometrycznych, które wyznaczały początki geometrii dedukcyjnej. Szkoła Pitagorejska kontynuowała to dzieło, a Platon (428 p. n. e.-348 p. n. e.) wyraźnie czerpie z pracy wcześniejszych matematyków, gdy wspomina o faktach geometrycznych w swoich pismach. Dialog geometryczny w jego pracy Meno, w którym Sokrates nakłania niewolnika do osiągnięcia twierdzenia geometrycznego za pomocą serii dedukcji logicznych, jest wart przeczytania. Jeśli pochodzenie geometrii jest niejasne, „produkt końcowy” nie jest. Euklid (323-283 p. n. e.), piszący w Aleksandrii, stworzył niezwykłe dzieło o nazwie elementy, które przez ponad 2000 lat pozostawało standardowym podręcznikiem geometrii. W tej pracy Euklid określa szereg definicji (np. dla punktów i linii), postulatów i pojęć powszechnych. (Obecnie nazywamy je aksjomatami.) Z nich logicznie rozwinął, w bardzo starannie dobranej kolejności, wiele twierdzeń, które ogólnie nazywamy geometrią euklidesową. Istnieje wiele innych wyników geometrycznych, takich jak twierdzenie Pappusa, które zostały odkryte po Euklidesie, ale nie są one ogólnie objęte w szkole średniej.
jeden z pięciu postulatów Euklidesa nie był tak oczywisty, jak się wydawało. Jedna z jego wersji, znana jako aksjomat Playfaira stwierdza, że: Biorąc pod uwagę linię  i punkt P, a nie na
i punkt P, a nie na  , istnieje jedna i tylko jedna linia równoległa do
, istnieje jedna i tylko jedna linia równoległa do  przechodząca przez P. w XIX wieku wielu matematyków zadało pytanie ” co się stanie, jeśli zaprzeczymy temu postulatowi?”Odbywa się to poprzez założenie, że albo nie ma takiej równoległej linii, albo przez powiedzenie, że istnieje więcej niż jedna taka linia. Doprowadziło to do rozwoju geometrii nie-euklidesowych, z których jedna okazała się jednym z dobrych modeli dla wszechświata.
przechodząca przez P. w XIX wieku wielu matematyków zadało pytanie ” co się stanie, jeśli zaprzeczymy temu postulatowi?”Odbywa się to poprzez założenie, że albo nie ma takiej równoległej linii, albo przez powiedzenie, że istnieje więcej niż jedna taka linia. Doprowadziło to do rozwoju geometrii nie-euklidesowych, z których jedna okazała się jednym z dobrych modeli dla wszechświata.
Aplikacje
w bardzo realnym sensie geometria i intuicja geometryczna stanowią podstawę wszystkich
matematyki − geometria prowadzi do geometrii współrzędnych, która prowadzi do rachunku różniczkowego i
wszystkich jej licznych zastosowań − i tak jest kluczowa w programie nauczania.
na bardziej praktycznym poziomie Budowniczowie, geodeci, inżynierowie i architekci są od wieków ciężkimi użytkownikami geometrii i idei geometrycznych. Ostatnio, wraz z rozwojem komputerów, graficy i projektanci stron internetowych dołączyli do tej grupy ludzi, którzy potrzebują i używają geometrii w swojej pracy. Zapytany niedawno, jak przydatna jest geometria, Jim Kelly, naukowiec zajmujący się zastosowaniami, powiedział: … geometria jest ważną częścią projektowania, rysunku i modelowania komputerowego. Jest również często używany w … zajęcia z fizyki i innych nauk fizycznych w ramach rozumienia wpływu obciążeń na struktury i punkty równoważenia (centra ciężkości) ciał stałych złożonych. W chemii zrozumienie geometrii cząsteczki jest związane ze zrozumieniem właściwości substancji. Istnieje o wiele więcej przykładów. (ze strony Ask a Scientist.
Historia matematyki: An Introduction, 3rd Edition, Victor J. Katz, Addison-Wesley, (2008)
History of Mathematics, D. E. Smith, Dover publications New York, (1958)
odpowiedzi do ćwiczeń
Ćwiczenie 1
ćwiczenie 2
punkty są zbieżne
ćwiczenie 3
60°
ćwiczenia 4
![]() DBA = 102° (odpowiednie kąty, AB / / CD)
DBA = 102° (odpowiednie kąty, AB / / CD)
![]() BAC = 78° (kąty co-wewnętrzne, AC||BD)
BAC = 78° (kąty co-wewnętrzne, AC||BD)
ćwiczenie 5
α = 65°![]() (kąty odpowiadające, AC||BM)
(kąty odpowiadające, AC||BM)
β = 80°![]() (kąty alternatywne, AC||BM)
(kąty alternatywne, AC||BM)
γ + β = 115°![]() (co-kąty wewnętrzne, AC||BM)
(co-kąty wewnętrzne, AC||BM)
= 35°
(jest to struktura dla dowodu wyniku, że suma kątów trójkąta wynosi 180°)
ćwiczenie 6
α = 60°
ćwiczenie 7
a![]() czworokąt z każdym z kątów wewnętrznych kąt prosty jest prostokątem.
czworokąt z każdym z kątów wewnętrznych kąt prosty jest prostokątem.
Converse: każdy kąt wewnętrzny prostokąta jest kątem prostym.
b![]() prostokąt to kwadrat
prostokąt to kwadrat
Konwersja: kwadrat to prostokąt
c![]() suma kątów wewnętrznych trójkąta wynosi 200°
suma kątów wewnętrznych trójkąta wynosi 200°
Konwersja: wielokąt, dla którego suma kąta wewnętrznego wynosi 200°, jest trójkątem.
ćwiczenie 8
α = 50°
ćwiczenie 9
odnosimy się do tego samego diagramu.
umieść punkt H na linii EF po lewej stronie E.
![]() CBE =
CBE = ![]() BEH
BEH
jeśli BC i EF nie są równoległe, narysuj BD równolegle do EF.
ponieważ BD i EF są równoległe, ![]() EBD=
EBD= ![]() BEH, co jest wyraźnie niemożliwe, chyba że linie BC i BD są takie same.
BEH, co jest wyraźnie niemożliwe, chyba że linie BC i BD są takie same.
stąd linie BC i EF są równoległe.
ćwiczenia 10
360°
projekt Improving Mathematics Education in Schools (TIMES) 2009-2011 został sfinansowany przez Australijski rządowy Departament Edukacji, zatrudnienia i Stosunków Pracy.
poglądy wyrażone tutaj są poglądami autora i niekoniecznie reprezentują poglądy australijskiego Departamentu Edukacji, zatrudnienia i Stosunków Pracy.
© Uniwersytet w Melbourne w imieniu Międzynarodowego Centrum Doskonałości Edukacji w matematyce (ICE-EM), Wydział Edukacji Australijskiego Instytutu Nauk Matematycznych (AMSI), 2010 (o ile nie zaznaczono inaczej). Ten utwór jest dostępny na licencji Creative Commons Uznanie autorstwa-Użycie niekomercyjne-Bez utworów zależnych 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()