ocena | Biopsychologia | porównawcza |kognitywna | rozwojowa | językowa | różnice indywidualne |osobowość | filozofia | społeczna |
metody | Statystyka |kliniczna | Edukacyjna | przemysłowa |zawodowa |świat psychologia |
Statystyka:Metoda naukowa · metody badawcze · projektowanie eksperymentalne · studia licencjackie statystyki · testy statystyczne · teoria gier · teoria decyzji
proszę o pomoc w samodzielnym ulepszeniu tej strony..
Analiza klastrów lub klastrowanie jest powszechną techniką analizy danych statystycznych, która jest stosowana w wielu dziedzinach, w tym w uczeniu maszynowym, eksploracji danych, rozpoznawaniu wzorców, analizie obrazów i bioinformatyce. Klastrowanie jest klasyfikacją podobnych obiektów na różne grupy, a dokładniej, dzieleniem zbioru danych na podzbiory (klastry), tak aby dane w każdym podzbiorze (najlepiej) miały wspólną cechę – często bliskość według określonej miary odległości.
poza terminem grupowanie danych (lub po prostu grupowanie) istnieje wiele terminów o podobnym znaczeniu, w tym analiza klastrów, Automatyczna klasyfikacja, Taksonomia numeryczna, botryologia i analiza typologiczna.
- rodzaje klastrowania
- grupowanie hierarchiczne
- miara odległości
- tworzenie klastrów
- aglomeracyjne grupowanie hierarchiczne
- grupowanie partycji
- K-oznacza i pochodne
- K-oznacza grupowanie
- algorytm Qt clust
- Fuzzy c-oznacza klastrowanie
- kryterium łokcia
- klastrowanie spektralne
- zastosowania
- Biologia
- badania marketingowe
- inne aplikacje
- porównania między klastrami danych
- Zobacz też
- Bibliografia
- implementacje oprogramowania
- darmowe
rodzaje klastrowania
algorytmy klastrowania danych mogą być hierarchiczne lub partycjonalne. Algorytmy hierarchiczne znajdują kolejne klastry przy użyciu wcześniej ustalonych klastrów, natomiast algorytmy partycjonujące określają wszystkie klastry jednocześnie. Algorytmy hierarchiczne mogą być aglomeracyjne (bottom-up) lub dzielące (top-down). Algorytmy aglomeracyjne rozpoczynają się od każdego elementu jako osobnego klastra i łączą je w kolejno większe klastry. Algorytmy dzielące zaczynają się od całego zbioru i przechodzą do dzielenia go na kolejno mniejsze skupiska.
grupowanie hierarchiczne
miara odległości
kluczowym krokiem w grupowaniu hierarchicznym jest wybranie miary odległości. Miarą prostą jest odległość Manhattanu, równa sumie odległości bezwzględnych dla każdej zmiennej. Nazwa pochodzi od faktu, że w przypadku dwóch zmiennych zmienne można wykreślić na siatce, którą można porównać do ulic miasta, a odległość między dwoma punktami to liczba bloków, które osoba przeszłaby.
bardziej powszechną miarą jest odległość euklidesowa, obliczana przez znalezienie kwadratu odległości między każdą zmienną, zsumowanie kwadratów i znalezienie pierwiastka kwadratowego tej sumy. W przypadku dwóch zmiennych odległość jest analogiczna do znalezienia długości przeciwprostokątnej w trójkącie; to znaczy jest to odległość ” w linii prostej.”Przegląd analizy klastrów w badaniach Psychologii Zdrowia wykazał, że najczęstszą miarą odległości w opublikowanych badaniach w tym obszarze badawczym jest odległość euklidesowa lub kwadratowa odległość euklidesowa.
tworzenie klastrów
biorąc pod uwagę miarę odległości, elementy można łączyć. Hierarchiczne klastrowanie buduje (aglomeracyjne) lub rozbija (dzielące) hierarchię klastrów. Tradycyjną reprezentacją tej hierarchii jest drzewiasta struktura danych (zwana dendrogramem), z pojedynczymi elementami na jednym końcu i pojedynczym klastrem z każdym elementem na drugim. Algorytmy aglomeracyjne zaczynają się na górze drzewa, natomiast algorytmy dzielące zaczynają się na dole. (Na rysunku strzałki oznaczają skupisko aglomeracyjne.)
przycinanie drzewa na danej wysokości da klastrowanie z wybraną precyzją. W poniższym przykładzie, cięcie po drugim wierszu da klastry {a} {b c} {d e} {f}. Cięcie po trzecim rzędzie daje klastry {a} {b c} {d E f}, które są grubszymi klastrami, z mniejszą liczbą większych klastrów.
aglomeracyjne grupowanie hierarchiczne
na przykład załóżmy, że te dane mają być grupowane. Gdzie odległość euklidesowa jest metryką odległości.
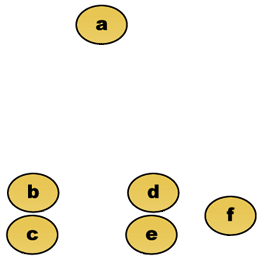
Dane surowe
hierarchiczny klastrujący dendrogram byłby jako taki:
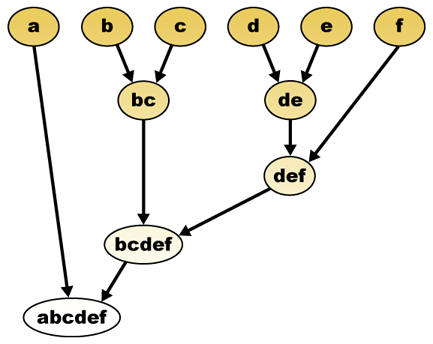
reprezentacja tradycyjna
metoda ta buduje hierarchię z poszczególnych elementów poprzez stopniowe łączenie klastrów. Ponownie, mamy sześć elementów {A} {b} {c} {d} {e} i {f}. Pierwszym krokiem jest określenie, które elementy połączyć w klastrze. Zazwyczaj chcemy wziąć dwa najbliższe elementy, dlatego musimy zdefiniować odległość 
Załóżmy, że połączyliśmy dwa najbliższe elementy b i c, mamy teraz następujące klastry {a}, {b, c}, {d}, {e} i {f} i chcemy je połączyć dalej. Ale aby to zrobić, musimy wziąć odległość między {A} i {b c}, a zatem zdefiniować odległość między dwoma klastrami. Zwykle odległość między dwoma klastrami 
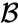
- maksymalna odległość między elementami każdego klastra (zwanego również kompletnym klastrem połączeń):
- minimalna odległość między elementami każdego klastra (zwanego również klastrem pojedynczego połączenia):
- średnia odległość między elementami każdego klastra (zwana również średnim klastrem wiązań):
- suma wszystkich wariancji wewnątrz klastra
- wzrost wariancji dla połączonego klastra (kryterium Warda)
- prawdopodobieństwo, że kandydujące klastry pojawią się z tej samej funkcji dystrybucyjnej (V-powiązanie)
każda aglomeracja występuje w większej odległości między klastrami niż poprzednia aglomeracja i można zdecydować się na zaprzestanie klastrowania, gdy klastry są zbyt daleko od siebie, aby można je było połączyć (kryterium odległości) lub gdy liczba klastrów jest wystarczająco mała (kryterium liczby).
grupowanie partycji
K-oznacza i pochodne
K-oznacza grupowanie
algorytm K-oznacza przypisuje każdy punkt do gromady, której środek (zwany także centroidem) jest najbliższy. Środek jest średnią wszystkich punktów w gromadzie-to znaczy jego współrzędne są średnią arytmetyczną dla każdego wymiaru oddzielnie dla wszystkich punktów w gromadzie.
przykład: Zbiór danych ma trzy wymiary, a klaster ma dwa punkty: X = (x1, x2, x3) I Y = (y1, y2, y3). Następnie centroid z staje się Z = (z1, Z2, z3), gdzie Z1 = (x1 + y1)/2 i Z2 = (x2 + y2)/2 i z3 = (x3 + y3)/2.
algorytm jest mniej więcej (J. MacQueen, 1967):
- losowo Generuj klastry k i określaj centra klastrów lub bezpośrednio Generuj punkty nasienne k jako centra klastrów.
- Przypisz każdy punkt do najbliższego centrum klastra.
- Przelicz nowe centra klastrów.
- powtarzaj, dopóki nie zostanie spełnione jakieś kryterium konwergencji (Zwykle, że przypisanie się nie zmieniło).
głównymi zaletami tego algorytmu jest jego prostota i szybkość, która pozwala mu działać na dużych zbiorach danych. Jego wadą jest to, że nie daje tego samego wyniku z każdym biegiem, ponieważ powstałe klastry zależą od początkowych losowych przydziałów. Maksymalizuje wariancję między klastrami (lub minimalizuje wariancję wewnątrz klastra), ale nie zapewnia, że wynik ma globalne minimum wariancji.
algorytm Qt clust
Qt (próg jakości) klastrowanie (Heyer i wsp., 1999) jest alternatywną metodą podziału danych, wynalezioną do klastrowania genów. Wymaga większej mocy obliczeniowej niż k-means, ale nie wymaga określania liczby klastrów a priori i zawsze zwraca ten sam wynik, gdy jest uruchamiany kilka razy.
algorytm jest:
- użytkownik wybiera maksymalną średnicę dla klastrów.
- Zbuduj klaster kandydata dla każdego punktu, włączając najbliższy punkt, najbliższy najbliższy itd., dopóki średnica klastra nie przekroczy progu.
- Zapisz klaster kandydata z największą liczbą punktów jako pierwszy prawdziwy klaster i usuń wszystkie punkty w klastrze z dalszej analizy.
- Rekurencja ze zmniejszonym zestawem punktów.
odległość między punktem a grupą punktów oblicza się za pomocą pełnego powiązania, tj. jako maksymalna odległość od punktu do dowolnego członka grupy (patrz sekcja „aglomeracyjne grupowanie hierarchiczne” dotycząca odległości między klastrami).
Fuzzy c-oznacza klastrowanie
w klastrach rozmytych każdy punkt ma stopień przynależności do klastrów, jak w logice rozmytej, a nie przynależności całkowicie do tylko jednego klastra. Tak więc punkty na krawędzi gromady mogą znajdować się w gromadzie w mniejszym stopniu niż punkty w centrum gromady. Dla każdego punktu x mamy współczynnik dający stopień bycia w klastrze kth 

z rozmytym c-oznacza, że centroid gromady jest średnią wszystkich punktów ważoną stopniem przynależności do gromady:
stopień przynależności jest związany z odwrotnością odległości do gromady
następnie współczynniki są znormalizowane i fuzzyfikowane z parametrem rzeczywistym 
dla m równego 2 jest to równoważne normalizacji współczynnika liniowo, aby ich suma była równa 1. Gdy m jest zbliżone do 1, wówczas Centrum skupienia najbliżej punktu otrzymuje znacznie większą wagę niż pozostałe, a algorytm jest podobny do K-oznacza.
algorytm C-means jest bardzo podobny do algorytmu k-means:
- wybierz kilka klastrów.
- Przypisz losowo do każdego punktu współczynniki bycia w klastrach.
- powtarzaj, aż algorytm się zbierze (to znaczy, że zmiana współczynników między dwiema iteracjami nie jest większa niż
, podany próg czułości) :
- Oblicz centroid dla każdego klastra, używając powyższego wzoru.
- dla każdego punktu Oblicz jego współczynniki bycia w klastrach, korzystając z powyższego wzoru.
algorytm minimalizuje również wariancję wewnątrz klastra, ale ma takie same problemy jak k-means, minimum jest lokalnym minimum, a wyniki zależą od początkowego wyboru wag.
kryterium łokcia
kryterium łokcia jest powszechną zasadą określającą, jaką liczbę klastrów należy wybrać, na przykład dla K-średniej i aglomeracyjnego hierarchicznego klastrowania.
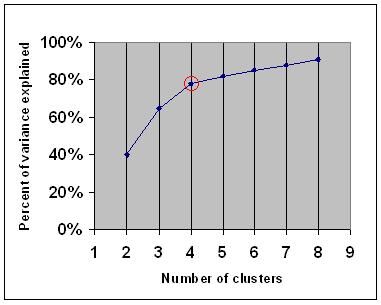
kryterium łokcia mówi, że należy wybrać liczbę klastrów, aby dodanie kolejnego klastra nie dodało wystarczających informacji. Dokładniej, jeśli narysujesz procent wariancji wyjaśnionej przez klastry w stosunku do liczby klastrów, pierwsze klastry dodadzą wiele informacji (wyjaśnią wiele wariancji), ale w pewnym momencie przyrost marginalny spadnie, dając kąt na wykresie (łokieć).
na poniższym wykresie łokieć jest oznaczony czerwonym kółkiem. Liczba wybranych klastrów powinna zatem wynosić 4.
klastrowanie spektralne
biorąc pod uwagę zbiór punktów danych, macierz podobieństwa może być zdefiniowana jako macierz {\displaystyle S} gdzie 
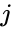
jedną z takich technik jest algorytm Shi-Malika, powszechnie stosowany do segmentacji obrazów. Dzieli punkty na dwa zestawy 
{\displaystyle S}, gdzie 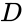
to partycjonowanie może być wykonane na różne sposoby, na przykład przez wzięcie mediany 

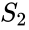
pokrewnym algorytmem jest algorytm Meila-Shi, który pobiera wektory własne odpowiadające K największym wartościom własnym macierzy 
zastosowania
Biologia
w biologii klastrowanie ma wiele zastosowań w dziedzinie biologii obliczeniowej i bioinformatyki, z których dwa to:
- w transkryptomice klastrowanie jest używane do budowania grup genów o powiązanych wzorach ekspresji. Często takie grupy zawierają funkcjonalnie powiązane białka, takie jak enzymy dla określonego szlaku lub geny, które są współregulowane. Eksperymenty o wysokiej przepustowości z wykorzystaniem wyrażonych znaczników sekwencji (est) lub mikromacierzy DNA mogą być potężnym narzędziem do adnotacji genomu, ogólnego aspektu genomiki.
- w analizie sekwencji, grupowanie jest używane do grupowania sekwencji homologicznych w rodziny genów. Jest to bardzo ważne pojęcie w bioinformatyce i biologii ewolucyjnej w ogóle. Zobacz ewolucję poprzez duplikację genów.
badania marketingowe
Analiza klastrów jest szeroko stosowana w badaniach rynku podczas pracy z wielowymiarowymi danymi z ankiet i paneli testowych. Badacze rynku wykorzystują analizę klastrową do podziału ogólnej populacji konsumentów na segmenty rynku i lepszego zrozumienia relacji między różnymi grupami konsumentów/potencjalnych klientów.
- Segmentacja rynku i wyznaczanie rynków docelowych
- pozycjonowanie produktów
- rozwój nowych produktów
- wybór rynków testowych (patrz : techniki eksperymentalne)
inne aplikacje
analiza sieci społecznościowych: w badaniu sieci społecznościowych klastrowanie może być używane do rozpoznawania społeczności w dużych grupach ludzi.
segmentacja obrazu: klastry mogą być używane do dzielenia obrazu cyfrowego na odrębne obszary w celu wykrywania granic lub rozpoznawania obiektów.
eksploracja danych: wiele aplikacji eksploracji danych obejmuje partycjonowanie elementów danych na powiązane podzbiory; aplikacje marketingowe omówione powyżej stanowią kilka przykładów. Innym powszechnym zastosowaniem jest podział dokumentów, takich jak strony internetowe World Wide Web, na gatunki.
porównania między klastrami danych
istnieje kilka sugestii dotyczących miary podobieństwa między dwoma klastrami. Taka miara może być użyta do porównania, jak dobrze różne algorytmy grupowania danych działają na zbiorze danych. Wiele z tych miar pochodzi z matching matrix (aka macierz pomieszania), np. miara Rand i miara Fowlkes-Mallows Bk.
- Jain, Murty and Flynn: Data Clustering: a Review, ACM Comp. Surv., 1999. Dostępne tutaj.
- dla innej prezentacji hierarchicznych, k-oznacza i rozmyte C-oznacza Patrz to wprowadzenie do klastrowania. Ma również wyjaśnienie dotyczące mieszania Gaussów.
- David Dowe, Mixture Modeling page-other clustering and mixture model links.
- samouczek na temat klastrowania
- Podręcznik on-line: Information Theory, Inference, and Learning Algorithms, autorstwa Davida J. C. Mackaya zawiera rozdziały na temat klastrowania k-means, miękkiego klastrowania k-means I pochodnych, w tym algorytmu E-M i wariacyjnego widoku algorytmu E-M.
Zobacz też
- k-means
- Sztuczna sieć neuronowa (ANN)
- Samoorganizująca się Mapa
- maksymalizacja oczekiwań (EM)
Bibliografia
- Clatworthy, J., Buick, D., Hankins, M., Weinman, J., & Horne, R. (2005). Zastosowanie i raportowanie analizy klastrowej w psychologii zdrowia: przegląd. British Journal of Health Psychology 10: 329-358.
- Romesburg, H. Clarles, Cluster Analysis for Researchers, 2004, 340 pp. ISBN 1411606175 lub wydawca, przedruk Wydania z 1990 roku wydanego przez Krieger Pub. Co… Tłumaczenie na język japoński jest dostępne w Uchida Rokakuho Publishing Co., Ltd., Tokio, Japonia.
- Heyer, L. J., Kruglyak, S. and Yooseph, S., Exploring Expression Data: Identification and Analysis of Coexpressed Genes, Genome Research 9: 1106-1115.
- Podręcznik on-line: Information Theory, Inference, and Learning Algorithms, autorstwa Davida J. C. Mackaya zawiera rozdziały na temat klastrowania k-means, miękkiego klastrowania k-means I pochodnych, w tym algorytmu E-M i wariacyjnego widoku algorytmu E-M.
do grupowania spektralnego :
- Jianbo Shi and Jitendra Malik, „Normalized Cuts and Image Segmentation”, IEEE Transactions on Pattern Analysis and Machine Intelligence, 22(8), 888-905, August 2000. Dostępne na stronie głównej Jitendra Malika
- Marina Meila i Jianbo Shi, „Learning Segmentation with Random Walk”, Neural Information Processing Systems, NIPS, 2001. Dostępne na stronie głównej Jianbo Shi
do szacowania liczby klastrów:
- Can, F., Ozkarahan, E. A. (1990) ” Concepts and effectiveness of the cover coefficient-based clustering methodology for text databases.”Transakcje ACM na systemach bazodanowych. 15 (4) 483-517.
implementacje oprogramowania
darmowe
- pakiet flexclust dla R
- YALE (Yet Another Learning Environment): darmowe oprogramowanie open-source do odkrywania wiedzy i eksploracji danych, zawierające również wtyczkę do klastrowania
- niektóre pliki źródłowe Matlab do klastrowania tutaj
- Compact – pakiet porównawczy do oceny klastrów (również w MATLAB)
- mixmod : Analiza Klastra Oparta Na Modelu I Analiza Dyskryminacyjna. Kod w C++, interfejs z Matlab i Scilab
- LingPipe Clustering Tutorial Tutorial do robienia klastrowania kompletnego i pojedynczego łącza za pomocą LingPipe, pakietu Java text data mining dystrybuowanego ze źródłem.
- WEKA : WEKA zawiera narzędzia do wstępnego przetwarzania danych, klasyfikacji, regresji, klastrowania, reguł asocjacji i wizualizacji. Doskonale nadaje się również do opracowywania nowych schematów uczenia maszynowego.