katamorfizm dla obu jest uogólnieniem jego fałdu. Katamorfizm umożliwia operacje niedostępne poprzez fold.
ten artykuł jest częścią serii artykułów o katamorfizmach. Katamorfizm jest uniwersalną abstrakcją, która opisuje, jak przetrawić strukturę danych w potencjalnie bardziej zwartą wartość.
Ten artykuł przedstawia katamorfizm dla obu (znany również jako wynik), a także jak go zidentyfikować. Początek artykułu przedstawia katamorfizm w języku C#, wraz z przykładami. Reszta artykułu opisuje jak wywnioskować katamorfizm. Ta część artykułu przedstawia moją pracę w Haskell. Czytelnicy, którzy nie czują się dobrze z Haskellem, mogą po prostu przeczytać pierwszą część, a resztę artykułu potraktować jako opcjonalny dodatek.
albo jest kontenerem danych, który modeluje dwa wzajemnie wykluczające się wyniki. Jest często używany do zwracania wartości, które mogą być poprawne (po prawej) lub Nieprawidłowe (po lewej). W statycznie typowanym programowaniu funkcyjnym z preferencją dla wszystkich funkcji, albo oferuje bardziej rozsądny, bardziej rozsądny sposób modelowania sukcesu i wyników błędów niż rzucanie WYJĄTKÓW.
C# katamorfizm #
ten artykuł używa kodowania kościelnego albo. Katamorfizmem dla obu jest metoda Match :
T Match<T>(Func<L, T> onLeft, Func<R, T> onRight);
do tego artykułu wszystkie poprzednie katamorfizmy były parą utworzoną z wartości początkowej i funkcji. Katamorfizm jest uogólnieniem, ponieważ jest parą funkcji. Jedna funkcja obsługuje przypadek, w którym jest lewa wartość, a druga funkcja obsługuje przypadek, w którym jest właściwa wartość. Obie funkcje muszą zwracać ten sam, unifikujący typ, który często jest ciągiem znaków lub czymś podobnym, co może być pokazane w interfejsie użytkownika:
> IEither<TimeSpan, int> e = new Left<TimeSpan, int>(TimeSpan.FromMinutes(3));> e.Match(ts => ts.ToString(), i => i.ToString())"00:03:00"> IEither<TimeSpan, int> e = new Right<TimeSpan, int>(42);> e.Match(ts => ts.ToString(), i => i.ToString())"42"
często zobaczysz przykłady, takie jak powyższy, które zamieniają zarówno lewe, jak i prawe przypadki w ciągi znaków lub coś, co może być reprezentowane jako jednoczący Typ odpowiedzi, ale nie jest to w żaden sposób wymagane. Jeśli możesz wymyślić Typ unifikujący, możesz przekonwertować oba przypadki na ten typ:
> IEither<Guid, string> e = new Left<Guid, string>(Guid.NewGuid());> e.Match(g => g.ToString().Count(c => 'a' <= c), s => s.Length)12> IEither<Guid, string> e = new Right<Guid, string>("foo");> e.Match(g => g.ToString().Count(c => 'a' <= c), s => s.Length)3
w dwóch powyższych przykładach używasz dwóch różnych funkcji, które redukują odpowiednio wartości Guid i string do liczby. Funkcja zamieniająca wartości Guid w liczbę zlicza liczbę szesnastkową większą lub równą A (10). Druga funkcja po prostu zwraca długość string, jeśli tam jest. Ten przykład nie ma sensu, ale metoda Match nie dba o to.
w praktycznym użyciu, albo jest często używany do obsługi błędów. Artykuł o kodowaniu Kościoła Zawiera przykład.
albo F-Algebra #
tak jak w poprzednim artykule, użyję Fix i cata jak wyjaśniono w doskonałym artykule Bartosza Milewskiego O F-Algebrach.
podczas gdy F-algebry i PUNKTY STAŁE są najczęściej używane dla rekurencyjnych struktur danych, można również zdefiniować F-algebrę dla nie-rekurencyjnej struktury danych. Widzieliście już przykład tego w artykułach o Katamorfizmie Boolowskim i być może katamorfizmie. Różnica między np. może wartości i albo jest taka, że oba przypadki albo mają wartość. Możesz modelować to jako Functor z zarówno typem nośnika, jak i dwoma argumentami typu dla danych, które mogą zawierać:
data EitherF l r c = LeftF l | RightF r deriving (Show, Eq, Read) instance Functor (EitherF l r) where fmap _ (LeftF l) = LeftF l fmap _ (RightF r) = RightF r
wybrałem wywołanie „typów danych” l (dla lewej) i r (dla prawej) oraz typ nośnika c (dla nośnika). Podobnie jak w przypadku BoolF i MaybeF, instancja Functor ignoruje funkcję map, ponieważ brakuje typu nośnika zarówno w przypadku LeftF, jak i RightF. Podobnie jak instancje Functor dla BoolF i MaybeF, wydawałoby się, że nic się nie dzieje, ale na poziomie typu jest to nadal tłumaczenie z EitherF l r c na EitherF l r c1. Może nie jest to zbyt duża funkcja, ale na pewno endofunktor.
podobnie jak w przypadku dedukowania katamorfizmów Maybe I List, Haskell nie jest zbyt zadowolony z definiowania instancji dla typu takiego jak Fix (EitherF l r). Aby rozwiązać ten problem, możesz wprowadzić opakowanie newtype :
newtype EitherFix l r = EitherFix { unEitherFix :: Fix (EitherF l r) } deriving (Show, Eq, Read)
możesz zdefiniować Functor, Applicative, Monad, itd. instancje tego typu bez uciekania się do żadnych rozszerzeń funky GHC. Należy pamiętać, że ostatecznie celem całego tego kodu jest tylko ustalenie, jak wygląda katamorfizm. Ten kod nie jest przeznaczony do rzeczywistego użytku.
para funkcji pomocniczych ułatwia definiowanie wartości EitherFix :
leftF :: l -> EitherFix l rleftF = EitherFix . Fix . LeftF rightF :: r -> EitherFix l rrightF = EitherFix . Fix . RightF
dzięki tym funkcjom możesz tworzyć wartości EitherFix :
Prelude Data.UUID Data.UUID.V4 Fix Either> leftF <$> nextRandomEitherFix {unEitherFix = Fix (LeftF e65378c2-0d6e-47e0-8bcb-7cc29d185fad)}Prelude Data.UUID Data.UUID.V4 Fix Either> rightF "foo"EitherFix {unEitherFix = Fix (RightF "foo")}
to wszystko, czego potrzebujesz, aby zidentyfikować katamorfizm.
Haskell catamorphism #
w tym momencie masz dwa z trzech elementów F-algebry. Masz endofunctor (EitherF l r) i obiekt c, ale nadal musisz znaleźć morfizm EitherF l r c -> c. Zauważ, że algebra, którą musisz znaleźć, Jest funkcją, która redukuje funktor do typu nośnika c, a nie „typy danych” li r. Przyzwyczajenie się do tego zajmuje trochę czasu, ale tak właśnie działają katamorfizmy. Nie oznacza to jednak, że możesz zignorować l i r, jak zobaczysz.
tak jak w poprzednich artykułach, zacznij od napisania funkcji, która stanie się katamorfizmem, opartym na cata:
eitherF = cata alg . unEitherFix where alg (LeftF l) = undefined alg (RightF r) = undefined
podczas gdy kompiluje się, z jego implementacjami undefined, oczywiście nie robi nic użytecznego. Uważam jednak, że pomaga mi to myśleć. Jak można zwrócić wartość typu c z przypadku LeftF? Możesz przekazać argument do funkcji eitherF :
eitherF fl = cata alg . unEitherFix where alg (LeftF l) = fl l alg (RightF r) = undefined
chociaż technicznie można przekazać argument typu c do eitherF, a następnie zwrócić tę wartość z przypadku LeftF, oznaczałoby to, że zignorowałbyś wartość l. Byłoby to niepoprawne, więc zamiast tego, Ustaw argument jako funkcję i wywołaj go za pomocą l. Podobnie, możesz zająć się sprawą RightF w ten sam sposób:
eitherF :: (l -> c) -> (r -> c) -> EitherFix l r -> ceitherF fl fr = cata alg . unEitherFix where alg (LeftF l) = fl l alg (RightF r) = fr r
to działa. Ponieważ cata ma typ Functor f => (f a -> a) -> Fix f -> a, oznacza to, że algma typ f a -> a. W przypadku EitherF kompilator wnioskuje, że funkcja alg ma typ EitherF l r c -> c, który jest właśnie tym, czego potrzebujesz!
możesz teraz zobaczyć, do czego służy typ nośnika c. Jest to typ, który algebra wyodrębnia, a więc typ, który zwraca katamorfizm.
to jest katamorfizm dla obu. Jak do tej pory było spójne, jest to para, ale teraz składa się z dwóch funkcji. Jak wielokrotnie widzieliście, nie jest to jedyny możliwy katamorfizm, ponieważ można na przykład trywialnie przerzucić argumenty na eitherF.
wybrałem reprezentację pokazaną tutaj, ponieważ jest izomorficzna z funkcją either z wbudowanego modułu Haskella Data.Either, który nazywa funkcję „analizą Przypadku dla typu Either„. Obie te funkcje (eitherF i either) są równoważne powyższej metodzie C# Match.
Basis #
większość innych przydatnych funkcji można zaimplementować za pomocą eitherF. Tu jest Bifunctor :
instance Bifunctor EitherFix where bimap f s = eitherF (leftF . f) (rightF . s)
z tej instancji, instancja Functor trywialnie następuje:
instance Functor (EitherFix l) where fmap = second
na górze Functor możesz dodać Applicative:
instance Applicative (EitherFix l) where pure = rightF f <*> x = eitherF leftF (<$> x) f
zauważ, że implementacja <*> jest podobna do implementacji <*> dla MaybeFix. To samo dotyczy instancji Monad :
instance Monad (EitherFix l) where x >>= f = eitherF leftF f x
nie tylko jest EitherFix Foldable, to Bifoldable:
instance Bifoldable EitherFix where bifoldMap = eitherF
zauważ, co ciekawe, że bifoldMap jest identyczny z eitherF.
wystąpienie Bifoldable umożliwia trywialne zaimplementowanie wystąpienia Foldable :
instance Foldable (EitherFix l) where foldMap = bifoldMap mempty
obecność mempty może być zagadkowa, ponieważ bifoldMap(lub eitherF; są identyczne) przyjmuje jako argumenty dwie funkcje. Czy mempty jest funkcją?
tak, mempty może być funkcją. Proszę. Istnieje instancja Monoid dla dowolnej funkcji a -> m, gdzie m jest instancją Monoid, a mempty jest tożsamością dla tego monoidu. To jest instancja w użyciu tutaj.
tak jak EitherFix to Bifoldable, to też Bitraversable:
instance Bitraversable EitherFix where bitraverse fl fr = eitherF (fmap leftF . fl) (fmap rightF . fr)
możesz wygodnie zaimplementować instancję Traversable w oparciu o instancję Bitraversable :
instance Traversable (EitherFix l) where sequenceA = bisequenceA . first pure
wreszcie, możesz zaimplementować konwersje do i ze standardowego typu Either, używając ana jako podwójnego cata:
toEither :: EitherFix l r -> Either l rtoEither = eitherF Left Right fromEither :: Either a b -> EitherFix a bfromEither = EitherFix . ana coalg where coalg (Left l) = LeftF l coalg (Right r) = RightF r
pokazuje to, że EitherFix jest izomorficzna z Either, co ponownie dowodzi, że eitherF i either są równoważne.
relacje #
w tej serii widzieliście różne przykłady katamorfizmów struktur, które nie mają fałd, katamorfizmów pokrywających się z fałdami, a teraz katamorfizm, który jest bardziej ogólny niż fałd. Wstępem do serii był poniższy schemat:
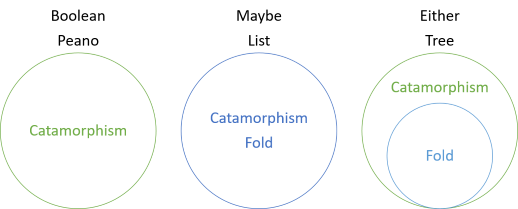
to pokazuje, że wartości logiczne i liczby Peano mają katamorfizm, ale nie ma fałd, podczas gdy dla Maybe I List, fold i katamorfizm są takie same. Dla obu jednak fałd jest szczególnym przypadkiem katamorfizmu. Fold dla obu „udaje”, że lewa strona nie istnieje. Zamiast tego lewa wartość jest interpretowana jako brakująca prawa wartość. Tak więc, aby spasować obie wartości, musisz podać wartość „awaryjną”, która zostanie użyta w przypadku, gdy obie wartości nie są poprawną wartością:
Prelude Fix Either> e = rightF LT :: EitherFix Integer OrderingPrelude Fix Either> foldr (const . show) "" e"LT"Prelude Fix Either> e = leftF 42 :: EitherFix Integer OrderingPrelude Fix Either> foldr (const . show) "" e""
w sesji GHCi, takiej jak powyższa, możesz utworzyć dwie wartości tego samego typu. Prawy przypadek to wartość Ordering, natomiast lewy przypadek to wartość Integer.
z foldr nie ma możliwości dostępu do lewej sprawy. Podczas gdy możesz uzyskać dostęp do właściwej wartości Ordering i przekształcić ją, liczba 42 jest po prostu ignorowana podczas składania. Zamiast tego zwracana jest wartość domyślna "".
kontrastuje to z katamorfizmem, który ma dostęp do obu przypadków:
Prelude Fix Either> e = rightF LT :: EitherFix Integer OrderingPrelude Fix Either> eitherF show show e"LT"Prelude Fix Either> e = leftF 42 :: EitherFix Integer OrderingPrelude Fix Either> eitherF show show e"42"
w takiej sesji odtwarzasz te same wartości, ale używając katamorfizmu eitherF, możesz teraz uzyskać dostęp i przekształcić zarówno lewy, jak i prawy przypadek. Innymi słowy, katamorfizm umożliwia wykonywanie operacji niemożliwych w przypadku zagięcia.
warto jednak zauważyć, że podczas gdy fałd jest specjalnością katamorfizmu, bifold jest identyczny z katamorfizmem.
podsumowanie #
katamorfizm dla obu jest parą funkcji. Jedna funkcja przekształca lewy przypadek, podczas gdy druga funkcja przekształca prawy przypadek. Dla dowolnej wartości zostanie użyta tylko jedna z tych funkcji.
kiedy po raz pierwszy zetknąłem się z pojęciem katamorfizmu, trudno mi było odróżnić katamorfizm od fałdowania. Moim problemem było, myślę, że samouczki, na które wpadłem, używały głównie połączonych list, aby pokazać, jak w tym przypadku fałd jest katamorfizmem. Okazuje się jednak, że nie zawsze tak jest. Katamorfizm jest abstrakcją ogólną. Z drugiej strony, fold wydaje mi się być głównie związany ze zbiorami.
w tym artykule zobaczyłeś pierwszy przykład katamorfizmu, który może zrobić więcej niż fałd. Dla obu, fałd jest tylko szczególnym przypadkiem katamorfizmu. Widziałeś też, jak katamorfizm był identyczny z bifoldem. Tak więc nadal nie jest do końca jasne, jak te pojęcia się odnoszą. Dlatego w następnym artykule przedstawimy przykład kontenera, w którym nie ma bifolda, a katamorfizm jest w istocie uogólnieniem fałdu.
następny: Katamorfizm drzew.