Antatt kunnskap
Studentene vil ha hatt omfattende uformell erfaring med geometri i tidligere år, og Dette vil gi et godt intuitivt grunnlag for den mer systematiske tilnærmingen til geometri som passer I År 7-10. De spesielle emnene Fra År F-6 relevant for denne modulen er:
- bruk av kompasser og linjaler og forsiktig tegning av geometriske figurer.
- typer vinkler, inkludert minst rette vinkler, spisse vinkler, stumpe vinkler og
refleksvinkler. - Trekanter, inkludert en uformell introduksjon til likebent og likesidet trekanter.
- Quadrilaterals, inkludert en uformell introduksjon til firkanter, rektangler, parallellogrammer, trapeser og rhombuses.
- Uformell erfaring med oversettelser, refleksjoner, rotasjoner og forstørrelser,
og med symmetri i sammenheng med aktiviteter som å brette en likebent trekant, rektangel eller rombe.
Motivasjon
 Geometri brukes til å modellere verden rundt oss. En visning av takene av hus avslører trekanter, trapes og rektangler, mens flislegging mønstre i fortau og bad bruke sekskanter, femkanter, trekanter og firkanter.
Geometri brukes til å modellere verden rundt oss. En visning av takene av hus avslører trekanter, trapes og rektangler, mens flislegging mønstre i fortau og bad bruke sekskanter, femkanter, trekanter og firkanter.
Byggherrer, flisleggere, arkitekter, grafiske designere og webdesignere bruker rutinemessig geometriske ideer i sitt arbeid. Klassifisere slike geometriske objekter og studere deres egenskaper er svært viktig. Geometri har også mange applikasjoner i kunst.
akkurat som aritmetikk har tall som sine grunnleggende objekter for studier, så er punkter, linjer og sirkler de grunnleggende byggesteinene i plangeometri.
i videregående geometri begynner vi med en rekke intuitive ideer (punkter, linjer og vinkler) som ikke er enkle å nøyaktig definere, etterfulgt av noen definisjoner (vertikalt motsatte vinkler, parallelle linjer og så videre) og fra disse utleder vi viktige fakta, som ofte refereres til som teoremer. I videregående skole bør nivået av strenghet utvikle seg sakte fra ett år til det neste, men i hvert trinn er klar innstilling svært viktig og bør understrekes.
dermed geometri gir en mulighet for elevene å utvikle sin geometriske intuisjon, som har programmer i mange områder av livet, og også å lære å konstruere logiske argumenter og gjøre fradrag i en innstilling som er, for det meste, uavhengig
av antall.
Innhold
Punkter Og Linjer
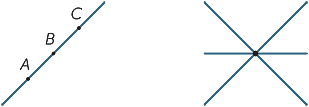
de enkleste objektene i plangeometri er punkter og linjer. Fordi de er så enkle, er det vanskelig å gi presise definisjoner av dem, så i stedet tar vi sikte på å gi studentene en grov beskrivelse av deres egenskaper som er i tråd med vår intuisjon. Et punkt markerer en posisjon, men har ingen størrelse. I praksis, når vi tegner et punkt, har det klart en bestemt bredde, men det representerer et punkt i fantasien vår. En linje har ingen bredde og strekker seg uendelig i begge retninger. Når vi tegner en linje, har den bredde og ender, så det er egentlig ikke en linje, men representerer en linje i fantasien vår. Gitt to forskjellige punkter A Og B så er det en (og bare en) linje som går gjennom begge punktene. Vi bruker store bokstaver for å referere til punkter og navnelinjer enten ved å angi to punkter på linjen, eller ved å bruke små bokstaver som  og m. dermed er den angitte linjen nedenfor referert til som linjen AB eller som linjen
og m. dermed er den angitte linjen nedenfor referert til som linjen AB eller som linjen  .
.

Gitt to forskjellige linjer, er det to muligheter: De kan enten møtes på et enkelt punkt eller de kan aldri møtes, uansett hvor langt de er utvidet (eller produsert). Linjer som aldri møtes kalles parallelle. I det andre diagrammet skriver VI AB / / CD.
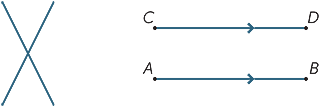
Tre (eller flere) punkter som ligger på en rett linje kalles kollineære.
Tre (eller flere) linjer som møtes på et enkelt punkt kalles samtidig.
|
|
|
| Kollineær |
Samtidig |
Øvelse 1
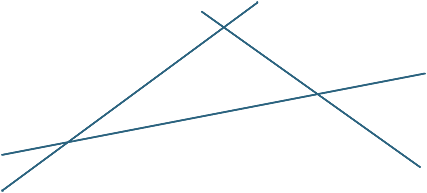
Tegn tre linjer som ikke er samtidige slik at ingen to er parallelle.
Øvelse 2
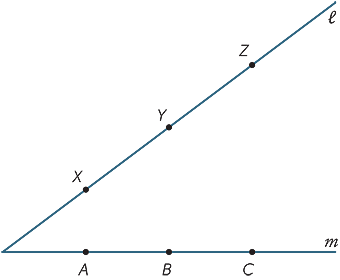
Lag en stor kopi av diagrammet nedenfor. Punktene X, Y, Z er noen punkter på linjen  og A, B, C er noen punkter på linjen m. Bli MED AY OG XB ring deres skjæringspunkt R. Bli MED BZ OG YC og ring deres skjæringspunkt P. Bli MED CX OG ZA og ring deres skjæringspunkt Q. hva merker du om punktene P, Q, R? (Dette resultatet kalles Pappus ‘ teorem, ca. 340 E.KR.)
og A, B, C er noen punkter på linjen m. Bli MED AY OG XB ring deres skjæringspunkt R. Bli MED BZ OG YC og ring deres skjæringspunkt P. Bli MED CX OG ZA og ring deres skjæringspunkt Q. hva merker du om punktene P, Q, R? (Dette resultatet kalles Pappus ‘ teorem, ca. 340 E.KR.)
Intervaller, Stråler Og Vinkler
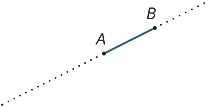 Anta At A og B er to punkter på en linje. Intervallet
Anta At A og B er to punkter på en linje. Intervallet
AB er delen av linjen Mellom A og B, inkludert de to endepunktene.
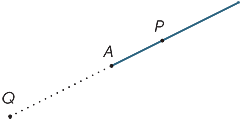 punktet A i diagrammet deler linjen i to deler kalt stråler. Strålen AP ER den strålen som inneholder punktet P (og punktet A).
punktet A i diagrammet deler linjen i to deler kalt stråler. Strålen AP ER den strålen som inneholder punktet P (og punktet A).
Vinkler
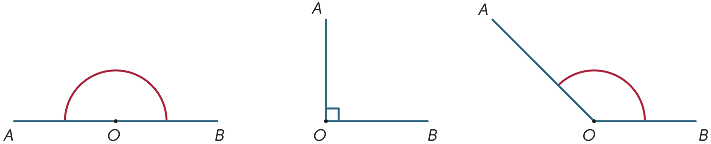
 i diagrammet kalles det skyggelagte området MELLOM strålene OA og OB vinkelen aob eller vinkelen BOA. Vinkeltegnet
i diagrammet kalles det skyggelagte området MELLOM strålene OA og OB vinkelen aob eller vinkelen BOA. Vinkeltegnet ![]() er skrevet så vi skriver
er skrevet så vi skriver ![]() AOB.
AOB.
 det skraverte området utenfor kalles refleksvinkelen dannet AV OA og OB. Mesteparten av tiden, med mindre vi angir ordrefleksen, refererer alle våre vinkler til området mellom strålene og ikke utenfor dem.
det skraverte området utenfor kalles refleksvinkelen dannet AV OA og OB. Mesteparten av tiden, med mindre vi angir ordrefleksen, refererer alle våre vinkler til området mellom strålene og ikke utenfor dem.
Størrelsen På En Vinkel
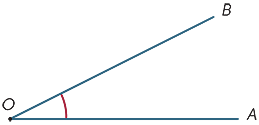 Tenk deg at ray OB roteres om punktet O til det ligger langs OA. Mengden sving kalles størrelsen på vinkelen AOB. Vi kan på samme måte definere størrelsen på refleksvinkelen.
Tenk deg at ray OB roteres om punktet O til det ligger langs OA. Mengden sving kalles størrelsen på vinkelen AOB. Vi kan på samme måte definere størrelsen på refleksvinkelen.
Vi vil ofte bruke små greske bokstaver, α, β ,γ.. for å representere størrelsen på en vinkel.
størrelsen på vinkelen som tilsvarer en full revolusjon ble delt (Av Babylonerne) i 360 like deler, som vi kaller grader. (De valgte sannsynligvis 360 siden det var nær antall dager i et år.) Størrelsen på en rett vinkel er derfor 180° og størrelsen på en rett vinkel er 90°. Andre vinkler kan måles (omtrentlig) ved hjelp av en grader.
|
|
||
| Rett vinkel | Rett vinkel |
Stump vinkel |
Vinkler er klassifisert i henhold til deres størrelse. Vi sier at en vinkel med størrelse α er akutt
(et ord som betyr ‘kvass’) hvis 0° < α < 90°, α er stumpe (et ord som betyr ‘butt’) hvis
90° < α < 180° og α er refleks hvis 180° < α < 360°.
siden vinkelmåleren har to skalaer, må elevene være forsiktige når de tegner og
målevinkler. Det er en verdig øvelse å bruke en grader til å tegne noen vinkler som 30°, 78°, 130°, 163°.
Øvelse 3
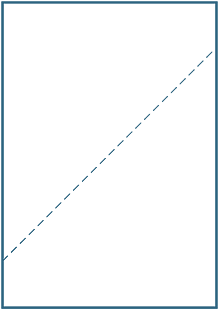 Brett et a4-ark som samsvarer med de (diagonalt) motsatte hjørnene. Tegn en linje langs krøllen som dannes og måle vinklene mellom krøllen og siden.
Brett et a4-ark som samsvarer med de (diagonalt) motsatte hjørnene. Tegn en linje langs krøllen som dannes og måle vinklene mellom krøllen og siden.
i øvelsen ovenfor danner de to vinklene sammen en rett linje og legger dermed til 180°. To vinkler som legger til 180° kalles tilleggsvinkler; dermed er 45° og 135° tilleggsvinkler.
to vinkler som legger til 90° kalles komplementære; dermed er 23° og 67°
komplementære vinkler.
Vinkler På Et Punkt
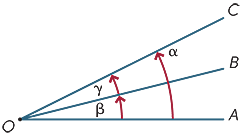 To vinkler på et punkt sies å være tilstøtende hvis de deler en felles stråle. Derfor, i diagrammet,
To vinkler på et punkt sies å være tilstøtende hvis de deler en felles stråle. Derfor, i diagrammet, ![]() AOB og
AOB og ![]() BOC er tilstøtende.
BOC er tilstøtende.
Tilstøtende vinkler kan legges til, så i diagrammet
α = β + γ.
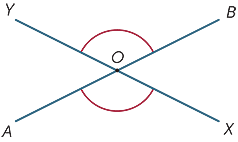
når to linjer krysser, dannes fire vinkler ved skjæringspunktet.
i diagrammet kalles vinklene merket ![]() AOX og
AOX og ![]() BOY vertikalt motsatt.
BOY vertikalt motsatt.
 Siden
Siden
-
 AOX er tillegget av
AOX er tillegget av  BOKS (rett vinkel).
BOKS (rett vinkel). -
 GUTT er også supplement til
GUTT er også supplement til  BOKS (rett vinkel),
BOKS (rett vinkel),
vi kan konkludere med at disse vertikalt motsatte vinklene,
![]() AOX og
AOX og ![]() BOY er like. Vi har dermed vår første
BOY er like. Vi har dermed vår første
viktige geometriske setning:
Vertikalt motsatte vinkler er like.
et resultat i geometri (og i matematikk generelt) kalles ofte et teorem. En teorem er en viktig setning som kan bevises ved logisk fradrag. Argumentet ovenfor er et bevis på teoremet; noen ganger presenteres bevis formelt etter setningen av teoremet.
 hvis to linjer krysser slik at alle fire vinkler er rette vinkler, sies linjene å være vinkelrett.
hvis to linjer krysser slik at alle fire vinkler er rette vinkler, sies linjene å være vinkelrett.
Vinkler ved et punkt-Geometriske Argumenter
følgende grunner kan brukes i geometriske argumenter:
- Tilstøtende vinkler kan legges til eller trekkes fra.
- Vinkler i en revolusjon legge til 360°
- Vinkler i en rett linje legger til 180 hryvnias.
- Vertikalt motsatte vinkler er like.
Transversale Og Parallelle Linjer
 en transversal er en linje som møter to andre linjer.
en transversal er en linje som møter to andre linjer.
Korresponderende vinkler
Ulike vinkler dannes av den transversale. I diagrammene nedenfor kalles de to merkede vinklene tilsvarende vinkler.
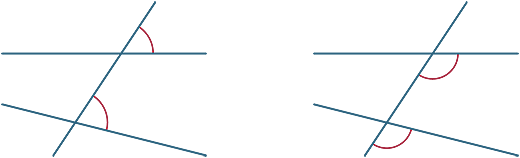
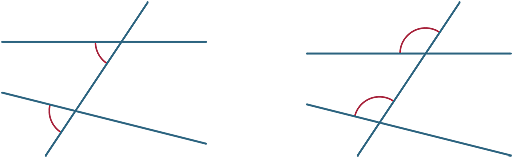
 Vi ser nå på hva som skjer når de to linjene kuttet av transversalen er parallelle.
Vi ser nå på hva som skjer når de to linjene kuttet av transversalen er parallelle.
Inituitively, hvis vinkelen α var større enn β deretter CD-ville krysse AB til venstre for F og om det var mindre enn β, det ville kryss til høyre for F. Så siden linjer kryss ikke i det hele tatt, α kan være verken mindre eller mer enn β og så β er lik.
alternativt kan du forestille deg å oversette vinkelen QGD langs GF til G faller sammen Med F. Siden linjene er parallelle, forventer vi at vinkelen α vil falle sammen med vinkelen β. Denne observasjonen fører oss til formodning om at:
Tilsvarende vinkler dannet fra parallelle linjer er like.
vi kan ikke bevise dette resultatet, selv om vi har vist at det er geometrisk plausibelt. Vi vil akseptere det som et aksiom av geometri. Et aksiom er en uttalelse som vi ikke kan bevise, men som er intuitivt rimelig. Merk at mange av de fakta vi allerede har nevnt som: tilstøtende vinkler kan legges, og to punkter bestemme en linje etc., er også aksiomer, selv om vi ikke eksplisitt har uttalt dem på denne måten.
Alternative Vinkler
i hvert diagram kalles de to merkede vinklene alternative vinkler(siden de er på alternative sider av transversalen).

 HVIS linjene AB og CD er parallelle, er de alternative vinklene like. Dette resultatet kan nå bevises.
HVIS linjene AB og CD er parallelle, er de alternative vinklene like. Dette resultatet kan nå bevises.
![]() dgq = α (korresponderende vinkler, AB / / CD)
dgq = α (korresponderende vinkler, AB / / CD)
![]() DGQ = β (vertikalt motsatte vinkler ved G)
DGQ = β (vertikalt motsatte vinkler ved G)
så α = β.
for å oppsummere:
Alternative Vinkler dannet fra parallelle linjer er like.
Co-interior Angles
Til slutt, i hvert diagram nedenfor, kalles de to merkede vinklene co-interior angles og ligger på samme side av transversalen.

HVIS LINJENE AB OG CD er parallelle, er det åpenbart at de innvendige vinklene ikke er like, men det viser seg at de er supplerende, det vil si at summen er 180° .
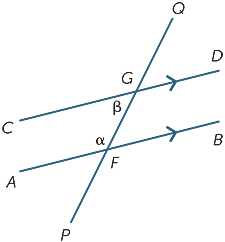 dette er et resultat som også er lett å bevise:
dette er et resultat som også er lett å bevise:
![]() bfg = β (alternative vinkler, AB ||CD)
bfg = β (alternative vinkler, AB ||CD)
α + β = 180° (rett vinkel på F)
for å oppsummere:
Sammenføyde vinkler dannet av parallelle linjer er supplerende.
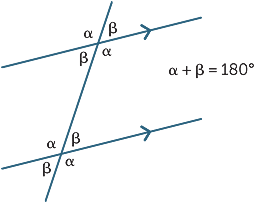 de tre resultatene kan oppsummeres
de tre resultatene kan oppsummeres
med følgende diagram:
Numeriske Eksempler
Gitt informasjon Om vinklene i et diagram, kan vi bruke resultatene ovenfor for å finne størrelsen på andre vinkler i diagrammet. Dette er en enkel, men svært viktig ferdighet, ofte referert til uformelt som vinkeljakt. Ved å løse problemer er trinnsekvensen ikke alltid unik. Det kan være flere forskjellige, men like gyldige, tilnærminger.
for eksempel, i det følgende diagrammet, søker vi størrelsen på vinkel BAC.

![]() DCA = 102° (alternative vinkler, AC / BD)
DCA = 102° (alternative vinkler, AC / BD)
![]() bac = 78° (med innvendige vinkler, AB||CD)
bac = 78° (med innvendige vinkler, AB||CD)
Øvelse 4
Bruk en alternativ sekvens av trinn for å finne ![]() BAC.
BAC.
Trening 5
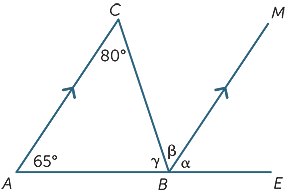 Bruk bare egenskaper for parallelle linjer, finn (med grunner) de manglende vinklene i følgende diagram.
Bruk bare egenskaper for parallelle linjer, finn (med grunner) de manglende vinklene i følgende diagram.
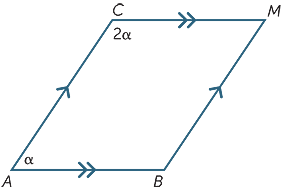
Øvelse 6
Finn verdien av α i diagrammet nedenfor.
Converse statements
Mange utsagn i matematikk har en converse, der implikasjonen går i motsatt retning. For eksempel setningen
‘ hver partall ender i 0, 2, 4, 6 eller 8.’
har converse
‘ Hvert tall som slutter på 0, 2, 4, 6 eller 8 er jevnt.’
denne spesielle setningen og dens omvendte er begge sanne, men dette er på ingen måte alltid
saken.
for eksempel er følgende to setninger samtaler av hverandre:
‘ Hvert multiplum av 4 er et jevnt tall.’
‘ hvert partall er et multiplum av 4.’
og her er den første setningen sant, men den andre er falsk.
Øvelse 7
Skriv ned:
a ![]() en sann geometrisk setning hvis converse er også sant,
en sann geometrisk setning hvis converse er også sant,
b ![]() falsk geometrisk setning hvis converse er sant,
falsk geometrisk setning hvis converse er sant,
c![]() en falsk geometrisk setning hvis converse er også falsk.
en falsk geometrisk setning hvis converse er også falsk.
De Omvendte Teoremene For Parallelle Linjer
vi har sett at tilsvarende vinkler dannet fra parallelle linjer er like. Vi kan skrive ned den omvendte setningen som følger.
Setning: hvis linjene er parallelle, er de tilsvarende vinklene like.
Converse: Hvis de tilsvarende vinklene er like, er linjene parallelle.
den omvendte setningen er også sant og brukes ofte til å bevise at to linjer er parallelle. Det samme gjelder med hensyn til alternative og co-indre vinkler.
Setning: hvis linjene er parallelle, er de alternative vinklene like.
Converse: hvis de alternative vinklene er like, er linjene parallelle.
Setning: hvis linjene er parallelle, er de co-indre vinklene supplerende.
Converse: Hvis de innvendige vinklene er supplerende, er linjene parallelle.
således er LINJENE AB og CD parallelle i hvert diagram.

Trening 8
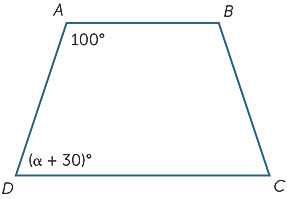 Hvilken verdi av α vil gjøre AB parallell MED CD?
Hvilken verdi av α vil gjøre AB parallell MED CD?
Bevis På De Tre Converses
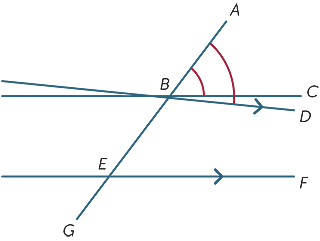 vi antar at de tilsvarende vinklene dannet av transversalen er like, og vi viser at linjene er parallelle.
vi antar at de tilsvarende vinklene dannet av transversalen er like, og vi viser at linjene er parallelle.
i diagrammet antar vi at
![]() ABC =
ABC = ![]() BEF.
BEF.
hvis BC og EF ikke er parallelle, tegner du
bd parallelt MED EF.
NÅ SIDEN BD og EF er parallelle ![]() ABD =
ABD = ![]() BEF og så
BEF og så ![]() ABC =
ABC = ![]() ABD som er klart umulig med mindre linjene BC og BD er de samme. DERFOR er LINJENE BC og EF parallelle.
ABD som er klart umulig med mindre linjene BC og BD er de samme. DERFOR er LINJENE BC og EF parallelle.
de andre bevisene følger på samme måte.
Øvelse 9
Gi et bevis på den andre omvendte setningen (alternative vinkler).
Vinkel sum av en trekant
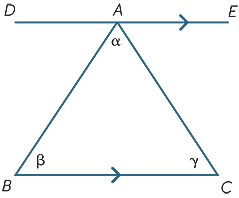 resultatene fra forrige avsnitt kan brukes til å utlede en av de viktigste fakta i geometri-vinkelen summen av en trekant er 180° .
resultatene fra forrige avsnitt kan brukes til å utlede en av de viktigste fakta i geometri-vinkelen summen av en trekant er 180° .
Vi begynner med trekant ABC med vinkler α, β, γ som vist. Tegn linjen dae parallelt MED BC. Deretter,
![]() dab = β (alternative vinkler, BC / / DE)
dab = β (alternative vinkler, BC / / DE)
![]() EAC = γ (alternerende vinkler, BC||DE)
EAC = γ (alternerende vinkler, BC||DE)
α+ β + γ = 180° (rett vinkel).
derfor har vi bevist teoremet
summen av vinklene i en trekant er 180°.
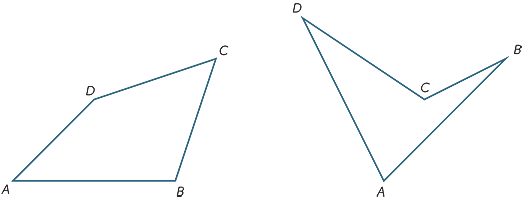
en firkant er en planfigur avgrenset av fire sider.
Øvelse 10
ved å dele den firkantede ABCD i to trekanter, finn summen av vinklene.
Links forward
materialet i denne modulen har begynt å plassere geometri på et rimelig systematisk grunnlag av nøye definerte objekter, aksiomer som skal antas, og teoremer som vi har bevist. På denne bakgrunn kan vi utvikle en systematisk redegjørelse for plangeometri som involverer:
- Pythagoras’ teorem
- kongruens og kongruente trekanter
- likhet og lignende trekanter
- isosceles og equilaterale trekanter
- spesielle firkanter, inkludert firkanter, rektangler, parallellogrammer, rhombuses og trapes
- geometrien av sirkler.
plangeometri vil også være grunnleggende i mange andre områder Av År 7-10 matematikk:
- transformasjoner
- tredimensjonal geometri
- områder og volumer
- trigonometri
- koordinatgeometri
- grafer av sirkler og parabler.
ideene til tangenter og områder fører igjen til kalkulator I År 11-12.
Historie Og Anvendelse
Historie
de utrolige konstruksjonene av pyramidene og De store templene I Egypt avslører At Egypterne må ha hatt en veldig god arbeidskunnskap og forståelse av grunnleggende geometri, i hvert fall på et praktisk nivå. På den annen side er det ingen bevis for at de hadde systematisert denne kunnskapen på noen formell måte. Dette ble overlatt til De gamle Grekerne. Vi har ikke detaljert kunnskap om at systematisering, bortsett fra påstanden Om At Thales (ca. 624 F KR.-ca. 546 F. KR.) ga de første bevisene på geometriske fakta som markerte begynnelsen på deduktiv geometri. Den Pythagoranske Skolen fortsatte dette arbeidet, Og Platon (428 F. KR. -348 F. KR.) trekker tydelig på arbeidet til tidligere matematikere når han nevner geometriske fakta i hans skrifter. Den geometriske dialogen I hans verk Meno, Hvor Sokrates får en slavegutt til å komme fram til et geometrisk teorem ved en rekke logiske fradrag, er verdt å lese. Hvis opprinnelsen til geometri er uklar, er sluttproduktet ikke. Euklid (323-283 F. KR.), som skrev I Alexandria, produserte et bemerkelsesverdig arbeid, kalt Elementene, som forblev standard lærebok i geometri i mer enn 2000 år. I dette arbeidet setter Euklid ut en rekke definisjoner (som for punkter og linjer), postulater og vanlige forestillinger. (I disse dager kaller vi dem aksiomer.) Fra disse utviklet han logisk, i en svært nøye utvalgt rekkefølge, mange teoremer som vi generelt refererer til Som Euklidisk Geometri. Det finnes en rekke andre geometriske resultater, slik Som Pappus’ teorem, som ble oppdaget etter Euklid, men disse er vanligvis ikke dekket i videregående skole.
En Av Euklids fem postulater var ikke så åpenbart sant som de andre syntes å være. En versjon av Det, kjent som Playfair Aksiom sier at: Gitt en linje og et punkt P, ikke på
og et punkt P, ikke på  , er det en og en linje parallell til
, er det en og en linje parallell til som går Gjennom P. I Det 19. århundre spurte en rekke matematikere spørsmålet ‘Hva skjer hvis vi nekter dette postulatet? Dette gjøres ved å anta at det enten ikke er en slik parallell linje, eller ved å si at det er mer enn en slik linje. Dette førte til utviklingen av ikke-euklidiske geometrier, hvorav en har vist seg å gi en av de gode modellene for universet.
som går Gjennom P. I Det 19. århundre spurte en rekke matematikere spørsmålet ‘Hva skjer hvis vi nekter dette postulatet? Dette gjøres ved å anta at det enten ikke er en slik parallell linje, eller ved å si at det er mer enn en slik linje. Dette førte til utviklingen av ikke-euklidiske geometrier, hvorav en har vist seg å gi en av de gode modellene for universet.
Applikasjoner
i en veldig reell forstand danner geometri og geometrisk intuisjon grunnlaget for Alle
Matematikk-geometri fører til koordinatgeometri som fører til kalkulator og
alle sine mange applikasjoner − og så er avgjørende i læreplanen.
på et mer praktisk nivå har byggherrer, landmålere, ingeniører og arkitekter vært tunge brukere av geometri og geometriske ideer i århundrer. Mer nylig, med utviklingen av datamaskiner, har grafikere og webdesignere blitt med i denne gruppen mennesker som trenger og bruker geometri i sitt arbeid. På spørsmål nylig hvor nyttig geometri er, Jim Kelly, en anvendt forsker sa:… geometri er en viktig del av design, tegning og datamodellering. Det brukes også ofte i … fysikk og andre fysiske vitenskapskurs som en del av å forstå effekten av belastninger på strukturer og balanseringspunkter(tyngdepunkter) for sammensatte faste stoffer. I kjemi er forståelse av geometrien til et molekyl relatert til å forstå egenskapene til stoffer. Mange flere eksempler finnes. (Fra Spør En Forsker nettsted.)
En Matematikkhistorie: En Introduksjon, 3. Utgave, Victor J. Katz, Addison-Wesley, (2008)
Matematikkens Historie, D. E. Smith, Dover publikasjoner New York, (1958)
SVAR PÅ ØVELSER
ØVELSE 1
ØVELSE 2
poeng I likhet kollineære
TRENING 3
60°
TRENING 4
![]() DBA = 102° (tilsvarende vinkler, AB||CD)
DBA = 102° (tilsvarende vinkler, AB||CD)
![]() BAC = 78° (co-indre vinklene, AC||BD)
BAC = 78° (co-indre vinklene, AC||BD)
ØVELSE 5
α = 65°![]() (tilsvarende vinkler, AC||BM)
(tilsvarende vinkler, AC||BM)
β = 80°![]() (alternative vinkler, AC||BM)
(alternative vinkler, AC||BM)
γ + β = 115°![]() (co-indre vinklene, AC||BM)
(co-indre vinklene, AC||BM)
Derfor, γ = 35°
(Dette er strukturen for et bevis på det resultat at vinkelen er summen av en trekant er 180°)
ØVELSE 6
α = 60°
ØVELSE 7
a![]() en firkant med hver av sine indre vinkler en rett vinkel er et rektangel.
en firkant med hver av sine indre vinkler en rett vinkel er et rektangel.
Converse: hver indre vinkel i et rektangel er en rett vinkel.
b ![]() et rektangel er et kvadrat
et rektangel er et kvadrat
Converse: et firkant er et rektangel
c ![]() vinkelsummen av de indre vinklene i en trekant er 200°
vinkelsummen av de indre vinklene i en trekant er 200°
Converse: et polygon hvor summen av den indre vinkelen er 200° er en trekant.
ØVELSE 8
α = 50°
ØVELSE 9
vi viser til det samme diagrammet.
Plasser et Punkt H PÅ LINJEN EF TIL venstre For E.
![]() CBE =
CBE = ![]() BEH
BEH
hvis BC og EF ikke er parallelle, tegner DU BD parallelt MED EF.
SIDEN BD og EF er parallelle, ![]() EBD=
EBD= ![]() BEH, som er klart umulig med mindre linjene BC og BD er de samme.
BEH, som er klart umulig med mindre linjene BC og BD er de samme.
derfor er linjene BC og EF parallelle.
ØVELSE 10
360°
The Improving Mathematics Education In Schools (TIMES) Prosjektet 2009-2011 ble finansiert av Den Australske Regjeringen Department Of Education, Sysselsetting Og Arbeidsplass Relasjoner.
synspunktene uttrykt her er de av forfatteren og representerer ikke nødvendigvis synspunktene Til Den Australske Regjeringen Department Of Education, Employment and Workplace Relations.
© Universitetet I Melbourne på vegne av International Centre Of Excellence For Utdanning I Matematikk (ICE-EM), utdanning divisjon Av Australian Mathematical Sciences Institute (AMSI), 2010 (unntatt der annet er angitt). Dette verk er lisensieret under følgende Creative Commons Navngivelse-Ikkekommersiell-Ingenbearbeidelser 3.0 unported Lisens.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()