I Dag vil det bli en kort introduksjon til sirkulær statistikk (noen ganger referert til som retningsstatistikk). Sirkulær statistikk er en interessant inndeling av statistikk som involverer observasjoner tatt som vektorer rundt en enhetssirkel. For eksempel, tenk å måle fødselstider på et sykehus over en 24-timers syklus, eller retningsmessig spredning av en gruppe trekkdyr. Denne typen data er involvert i en rekke felt, for eksempel økologi, klimatologi og biokjemi. Naturen til å måle observasjoner rundt en enhetssirkel krever en annen tilnærming til hypotesetesting. Fordelinger må «pakkes» rundt sirkelen for å være i bruk, og konvensjonelle estimatorer som prøvemiddelverdien eller prøvevariansen holder ikke vann.
I dette innlegget vil Vi gjennomføre Raos Avstandstest for å vurdere ensartetheten til et sirkulært datasett. Dette er en grunnleggende prosedyre og bør betraktes som en introduksjon til håndtering av sirkulære data.
Komme i gang
vi skal gjennomføre en hypotesetest på skilpadder, et lite datasett som består av ankomstvinklene på 10 grønne havskilpadder til deres nestende øy. Vårt mål er å finne ut hvor ankomst vinkler viser tegn til retning eller er mer indikativ for en tilfeldig scatter.
først installerer du circular – pakken og legger til turtles-datasettet.
install.packages("circular")require(circular)attach(turtles)
Plotting av dataene
circularpakken inneholder sin egen plotting-funksjon, plot.circular. La oss observere ankomst vinkler av skilpadder.
plot.circular(arrival)
her er plottet: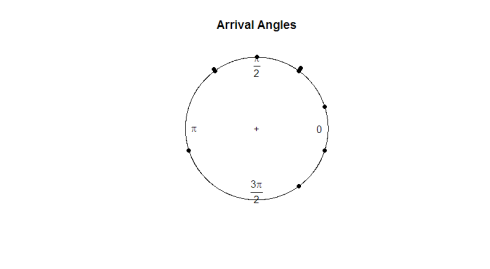
Gitt øyetesten ser observasjonene ut til å være ensartede rundt sirkelen. Hvis vi vil kjøre en hypotesetest for å avgjøre om dataene er virkelig ensartede, må vi utvikle en teststatistikk som fungerer med vinkeldata.
Hva er en god parameter for oss å utnytte? Å ta prøven betyr ikke mye om retningen av dataene (180 grader er ikke et nyttig gjennomsnitt på 2 grader og 358 grader). I det følgende plottet, observere hvordan utvalgsgjennomsnittet ikke er til nytte for å representere formen eller spredningen av dataene våre.
mean(arrival)plot.circular(mean(arrival)) 0.9120794
her er plottet: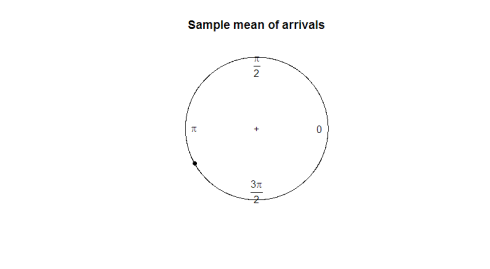
I Stedet vil vi bruke en metode som bestemmer retningen ved å måle gjennomsnittlig mellomrom mellom observasjoner. Denne testen kalles Raos Avstandstest.
Raos Avstandstest
Raos Avstandstest ble utviklet for å vurdere ensartethet av sirkulære data. Den bruker avstanden mellom observasjoner for å avgjøre om dataene viser betydelig retning. Hvis dataene er ensartede, bør observasjonene ha en tendens til å være jevnt fordelt.
Her er teststatistikken \(U\) For Raos Avstandstest: $ $ U = 1/2 \ sum \ limits_{i = 1}^n| T_{i} – λ/ $ $ hvor \(λ = 360 / n, t_{i} = f_{i+1}-f_{i}\) og \(T_{n} = (360-f_{n}) + f_{1}\)
i utgangspunktet aggregerer teststatistikken avvikene mellom påfølgende punkter, hver vektet av totalt antall observasjoner i datasettet.
Vi vil bruke funksjonen rao.spacing.test() til å kjøre denne hypotesetesten. Vår nullhypotese sier at dataene har en jevn fordeling, mens de alternative statene viser dataene tegn på retningsvirkning. La oss kjøre testen.
rao.spacing.test(arrival,alpha=.10) Rao's Spacing Test of Uniformity Test Statistic = 127.2689 Level 0.1 critical value = 161.23 Do not reject null hypothesis of uniformity
med en teststatistikk på 127 som faller under den kritiske verdien av 161, unnlater dataene å lene seg betydelig i alle retninger. Vi kan ikke avvise hypotesen om at skilpadder ankomster er av en jevn fordeling.
Konklusjon
Raos avstandstest bestemte at dataene ikke viste tegn på retningstrender. Vi kan ikke avvise nullhypotesen om ensartethet og vil anta ensartethet i forhold til ankomstretningen. Selv om dette innlegget var en relativt grunnleggende opplæring, har mange mennesker i datavitenskapssamfunnet ikke jobbet med sirkulære data før. Det er et interessant underemne å dykke inn i, så vel som et ungt felt av statistikk som fortsatt utvikler seg.
Avsluttende bemerkninger
jeg vil gjerne gi Kreditt Til S. Rao Jammalamadaka PhD, Ved University Of California, Santa Barbara, og hans lærebok «Emner I Sirkulær Statistikk» for å vekke min interesse for feltet sirkulær statistikk.