4.2 Estimering Av Koeffisientene Til Den Lineære Regresjonsmodellen / Introduksjon til Økonometri Med R

4.2 Estimering Av Koeffisientene Til Den Lineære Regresjonsmodellen

i praksis er intercept $\beta_0$ og helling $\beta_1$ av populasjonsregresjonslinjen ukjent. Derfor må vi bruke data for å estimere begge ukjente parametere. I det følgende vil et ekte verdenseksempel bli brukt til å demonstrere hvordan dette oppnås. Vi ønsker å relatere testresultater til student-lærerforhold målt i Californiske skoler. Testresultatet er det gjennomsnittlige gjennomsnittet for lesing og matematikk for femte gradere. Igjen måles klassestørrelsen som antall studenter dividert med antall lærere (student-lærerforholdet). Når det gjelder dataene, Kommer California School data set (CASchools) med En R-pakke kalt AER, et akronym For Applied Econometrics with R (Kleiber and Zeileis 2020). Etter installasjon av pakken med installasjon.pakker («AER») og feste den med bibliotek (AER) datasettet kan lastes ved hjelp av funksjonen data ().

## # install the AER package (once)## install.packages("AER")## ## # load the AER packagelibrary(AER)# load the the data set in the workspacedata(CASchools)

Når en pakke er installert, er den tilgjengelig for bruk ved flere anledninger når den påberopes med library ().pakker () igjen!

det er interessant å vite hva slags objekt vi har å gjøre med.klasse () returnerer klassen til et objekt. Avhengig av klassen av et objekt noen funksjoner (for eksempel plot() og sammendrag()) oppfører seg annerledes.

la oss sjekke klassen av objektet CASchools.

class(CASchools)#> "data.frame"

Det viser seg At CASchools er av klassedata.ramme som er et praktisk format å jobbe med, spesielt for å utføre regresjonsanalyse.

ved hjelp av head () får vi en første oversikt over våre data. Denne funksjonen viser bare de forste 6 radene i datasettet som forhindrer en overfylt konsollutgang.

trykk ctrl + L for å tømme konsollen. Denne kommandoen sletter all kode som er skrevet inn og utført av Deg eller skrevet ut til konsollen av R functions. Den gode nyheten er at alt annet er uberørt. Du mister heller ikke definerte variabler etc. heller ikke kodehistorien. Det er fortsatt mulig å huske tidligere utførte r-kommandoer ved hjelp av opp-og ned-tastene. Hvis Du arbeider I RStudio, trykker du ctrl + Opp på tastaturet (CMD + Opp På En Mac) for å se gjennom en liste over tidligere angitte kommandoer.

head(CASchools)#> district school county grades students teachers#> 1 75119 Sunol Glen Unified Alameda KK-08 195 10.90#> 2 61499 Manzanita Elementary Butte KK-08 240 11.15#> 3 61549 Thermalito Union Elementary Butte KK-08 1550 82.90#> 4 61457 Golden Feather Union Elementary Butte KK-08 243 14.00#> 5 61523 Palermo Union Elementary Butte KK-08 1335 71.50#> 6 62042 Burrel Union Elementary Fresno KK-08 137 6.40#> calworks lunch computer expenditure income english read math#> 1 0.5102 2.0408 67 6384.911 22.690001 0.000000 691.6 690.0#> 2 15.4167 47.9167 101 5099.381 9.824000 4.583333 660.5 661.9#> 3 55.0323 76.3226 169 5501.955 8.978000 30.000002 636.3 650.9#> 4 36.4754 77.0492 85 7101.831 8.978000 0.000000 651.9 643.5#> 5 33.1086 78.4270 171 5235.988 9.080333 13.857677 641.8 639.9#> 6 12.3188 86.9565 25 5580.147 10.415000 12.408759 605.7 605.4

vi finner at datasettet består av mange variabler, og at de fleste er numeriske.

forresten: et alternativ til klasse() og hode() er str() som er utledet fra ‘struktur’ og gir en omfattende oversikt over objektet. Prøv!

Vender tilbake Til CASchools, de to variablene vi er interessert i (dvs., gjennomsnittlig test score og student-lærer ratio) er ikke inkludert. Det er imidlertid mulig å beregne både fra de angitte dataene. For å oppnå student-lærerforholdene deler vi bare antall studenter med antall lærere. Gjennomsnittlig testresultat er det aritmetiske gjennomsnittet av testresultatet for lesing og poengsummen til matteprøven. Den neste kodebiten viser hvordan de to variablene kan konstrueres som vektorer og hvordan de legges til CASchools.

# compute STR and append it to CASchoolsCASchools$STR <- CASchools$students/CASchools$teachers # compute TestScore and append it to CASchoolsCASchools$score <- (CASchools$read + CASchools$math)/2

hvis vi kjørte hodet (CASchools) igjen, ville vi finne de to variablene av interesse som flere kolonner KALT STR og score (sjekk dette!).

Tabell 4.1 fra læreboken oppsummerer fordelingen av testresultater og student-lærerforhold. Det finnes flere funksjoner som kan brukes til å produsere lignende resultater, f. eks.,

gjennomsnitt () (beregner det aritmetiske gjennomsnittet av de angitte tallene),
sd () (beregner standardavviket for prøven),
quantile () (returnerer en vektor av de angitte utvalgskantantene for dataene).

den neste kodebiten viser hvordan man oppnår dette. Først beregner vi sammendragsstatistikk på kolonnene STR og score På CASchools. For å få fin utgang samler vi tiltakene i en data.ramme kalt DistributionSummary.

# compute sample averages of STR and scoreavg_STR <- mean(CASchools$STR) avg_score <- mean(CASchools$score)# compute sample standard deviations of STR and scoresd_STR <- sd(CASchools$STR) sd_score <- sd(CASchools$score)# set up a vector of percentiles and compute the quantiles quantiles <- c(0.10, 0.25, 0.4, 0.5, 0.6, 0.75, 0.9)quant_STR <- quantile(CASchools$STR, quantiles)quant_score <- quantile(CASchools$score, quantiles)# gather everything in a data.frame DistributionSummary <- data.frame(Average = c(avg_STR, avg_score), StandardDeviation = c(sd_STR, sd_score), quantile = rbind(quant_STR, quant_score))# print the summary to the consoleDistributionSummary#> Average StandardDeviation quantile.10. quantile.25. quantile.40.#> quant_STR 19.64043 1.891812 17.3486 18.58236 19.26618#> quant_score 654.15655 19.053347 630.3950 640.05000 649.06999#> quantile.50. quantile.60. quantile.75. quantile.90.#> quant_STR 19.72321 20.0783 20.87181 21.86741#> quant_score 654.45000 659.4000 666.66249 678.85999

når det gjelder eksempeldataene, bruker vi plot (). Dette tillater oss å oppdage egenskaper av våre data, for eksempel uteliggere som er vanskeligere å oppdage ved å se på bare tall. Denne gangen legger vi til noen ekstra argumenter til call of plot ().

det første argumentet i vår call of plot(), score ~ STR, er igjen en formel som angir variabler på y – og x-aksen. Men denne gangen lagres de to variablene ikke i separate vektorer, men er kolonner av CASchools. Derfor Vil R ikke finne dem uten at argumentdataene er riktig angitt. dataene må være i samsvar med navnet på dataene.ramme som variablene tilhører, i dette tilfellet CASchools. Ytterligere argumenter brukes til å endre utseendet på plottet: mens main legger til en tittel, legger xlab og ylab til egendefinerte etiketter i begge aksene.

plot(score ~ STR, data = CASchools, main = "Scatterplot of TestScore and STR", xlab = "STR (X)", ylab = "Test Score (Y)")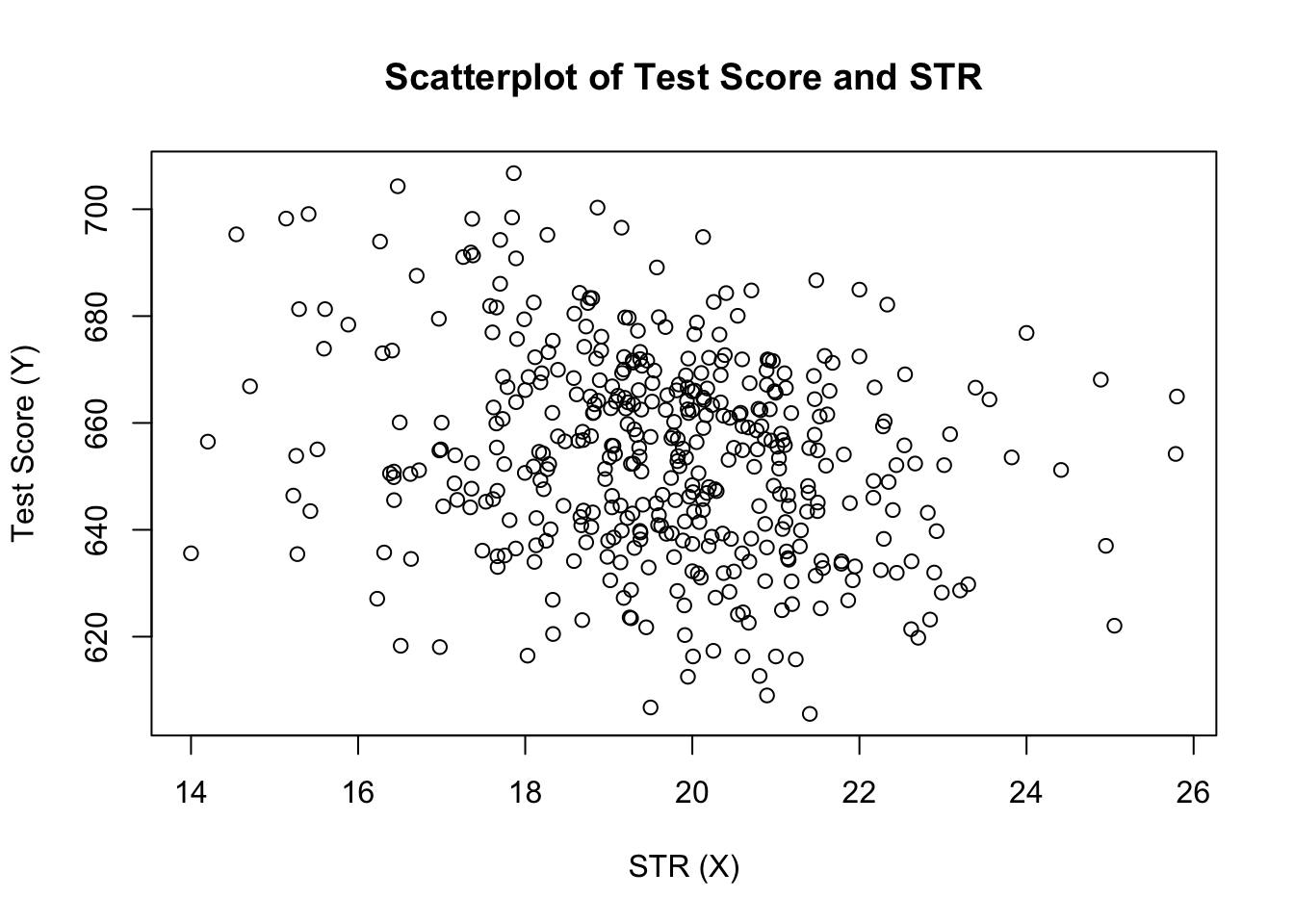

plottet (Figur 4.2 i boken) viser scatterplot av alle observasjoner på student-lærerforholdet og testresultatet. Vi ser at punktene er sterkt spredt, og at variablene er negativt korrelert. Det vil si at vi forventer å observere lavere testresultater i større klasser.

funksjonen cor () (se ?cor for ytterligere info) kan brukes til å beregne korrelasjonen mellom to numeriske vektorer.

cor(CASchools$STR, CASchools$score)#> -0.2263627

som scatterplot allerede antyder, er korrelasjonen negativ, men ganske svak.

oppgaven vi nå står overfor er å finne en linje som passer best til dataene. Selvfølgelig kan vi bare holde fast med grafisk inspeksjon og korrelasjonsanalyse og deretter velge den beste tilpasningslinjen ved å eyeballing. Dette ville imidlertid være ganske subjektivt: ulike observatører ville tegne forskjellige regresjonslinjer. På denne kontoen er vi interessert i teknikker som er mindre vilkårlig. En slik teknikk er gitt ved ordinær minste kvadraters (OLS) estimering.

Den Ordinære Minste Kvadraters Estimator

OLS-estimatoren velger regresjonskoeffisientene slik at den estimerte regresjonslinjen er så «nær» som mulig til de observerte datapunktene. Her måles nærhet av summen av de kvadrerte feilene som er gjort ved å forutsi $Y$ gitt \ (X\). La $b_0$ og\ (b_1\) være noen estimatorer av $\beta_0$ og $\beta_1$. Da kan summen av kvadrerte estimeringsfeil uttrykkes som

OLS-estimatoren i den enkle regresjonsmodellen er paret estimatorer for avskjæring og helling som minimerer uttrykket ovenfor. Avledningen AV OLS-estimatorene for begge parametrene er presentert i Vedlegg 4.1 i boken. Resultatene er oppsummert I Nøkkelbegrep 4.2.

OLS-Estimatoren, Forutsagte Verdier Og Residualer

OLS-estimatorene for skråningen $\beta_1$ og skjæringspunktet $\beta_0$ i den enkle lineære regresjonsmodellen er\OLS-spådde verdier $\widehat{Y}_i$ og residualer $\hat{u}_i$ er\

estimert skjæringspunkt $\hat{\beta}_0$, stigningsparameteren $\hat{\BETA}_1$ og Residualene $\Venstre(\Hat{U}_i\HØYRE)$ beregnes ut fra et utvalg av $n$ observasjoner av $x_i$ og $y_i$, $i$, $…$, $og$. Dette er estimater av den ukjente populasjonsavsnittet $\left (\beta_0 \ right)$, slope $\left (\beta_1 \ right)$ og error term $(u_i)$.

formlene som presenteres ovenfor, er kanskje ikke veldig intuitive ved første øyekast. Følgende interaktive programmet har som mål å hjelpe deg å forstå mekanikken I OLS. Du kan legge til observasjoner ved å klikke inn i koordinatsystemet der dataene er representert av poeng. Når to eller flere observasjoner er tilgjengelige, beregner programmet en regresjonslinje ved HJELP AV OLS og noen statistikk som vises i høyre panel. Resultatene oppdateres når du legger til ytterligere observasjoner i venstre panel. Et dobbeltklikk tilbakestiller programmet, dvs. alle data fjernes.

det er mange mulige måter å beregne $\hat {\beta}_0$ og $\hat {\beta}_1$ I R. for eksempel kan vi implementere formlene presentert i Nøkkelbegrep 4.2 med To Av Rs mest grunnleggende funksjoner: middel () og sum (). Før du gjør det, legger vi Til CASchools datasett.

attach(CASchools) # allows to use the variables contained in CASchools directly# compute beta_1_hatbeta_1 <- sum((STR - mean(STR)) * (score - mean(score))) / sum((STR - mean(STR))^2)# compute beta_0_hatbeta_0 <- mean(score) - beta_1 * mean(STR)# print the results to the consolebeta_1#> -2.279808beta_0#> 698.9329

Calling attach (CASchools) gjør det mulig for oss å adressere en variabel som finnes i CASchools ved navn: det er ikke lenger nødvendig å bruke $ – operatøren i forbindelse med datasettet: R kan evaluere variabelnavnet direkte.

r bruker objektet i brukermiljøet hvis dette objektet deler navnet på variabelen i en vedlagt database. Det er imidlertid en bedre praksis å alltid bruke særegne navn for å unngå slike (tilsynelatende) ambivalenser!

Legg Merke til at vi adresserer variabler som finnes i vedlagte datasett CASchools direkte for resten av dette kapitlet!

selvfølgelig er det enda flere manuelle måter å utføre disse oppgavene på. MED OLS som en av de mest brukte estimeringsteknikkene, inneholder R selvfølgelig allerede en innebygd funksjon kalt lm () (lineær modell) som kan brukes til å utføre regresjonsanalyse.

det første argumentet for funksjonen som skal spesifiseres er, lik plot(), regresjonsformelen med den grunnleggende syntaksen y ~ x hvor y er den avhengige variabelen og x den forklarende variabelen. Argumentdataene bestemmer datasettet som skal brukes i regresjonen. Vi ser nå eksemplet fra boken der forholdet mellom testresultatene og klassestørrelsene analyseres. Følgende kode bruker lm() for å gjenskape resultatene som presenteres i figur 4.3 i boken.

# estimate the model and assign the result to linear_modellinear_model <- lm(score ~ STR, data = CASchools)# print the standard output of the estimated lm object to the console linear_model#> #> Call:#> lm(formula = score ~ STR, data = CASchools)#> #> Coefficients:#> (Intercept) STR #> 698.93 -2.28

La oss legge til den estimerte regresjonslinjen til plottet. Denne gangen forstørrer vi også områdene til begge aksene ved å sette argumentene xlim og ylim.

# plot the dataplot(score ~ STR, data = CASchools, main = "Scatterplot of TestScore and STR", xlab = "STR (X)", ylab = "Test Score (Y)", xlim = c(10, 30), ylim = c(600, 720))# add the regression lineabline(linear_model)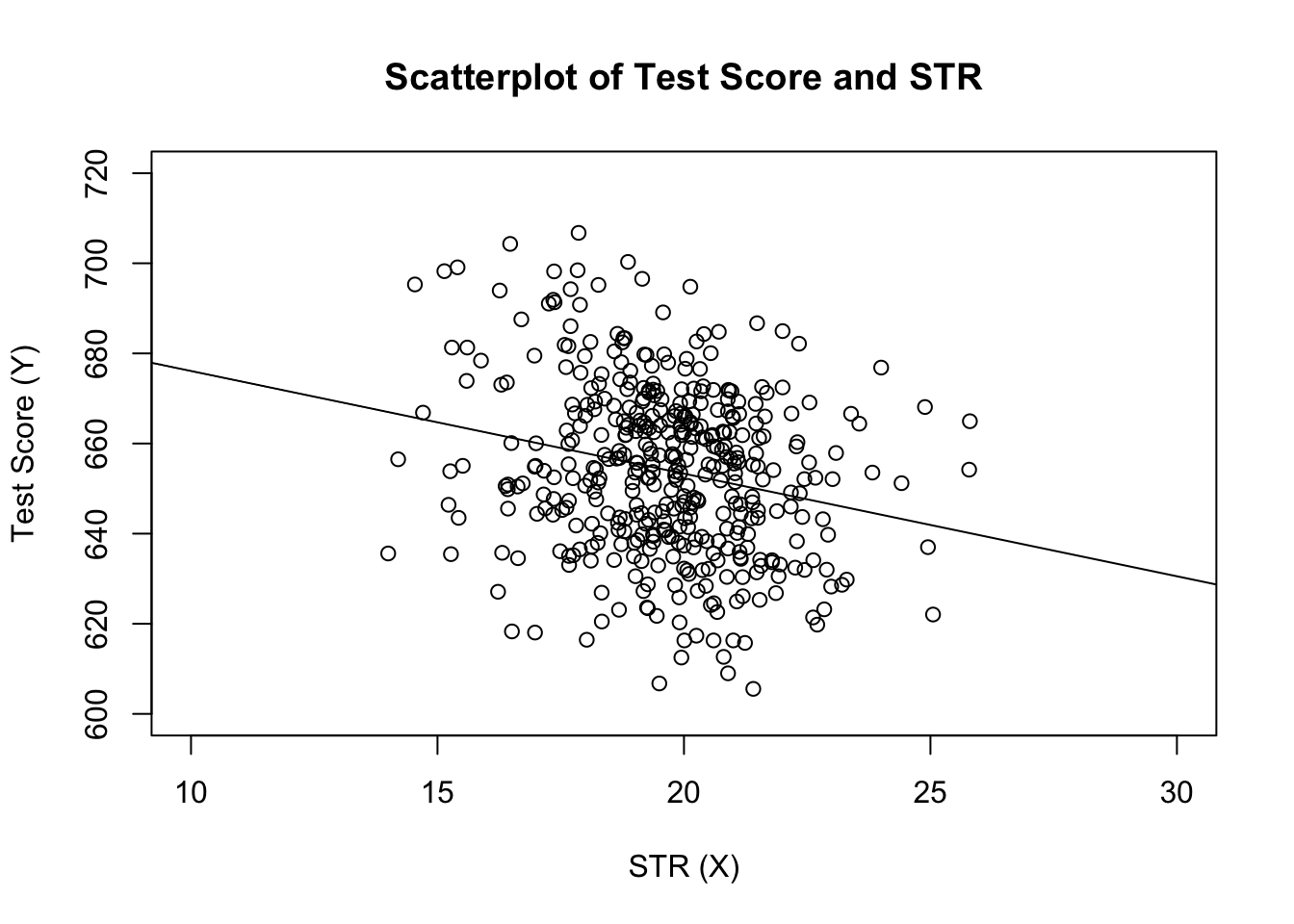

La du merke til at denne gangen passerte vi ikke avskjærings-og hellingsparametrene til abline? Hvis du kaller abline () på et objekt av klasse lm som bare inneholder en enkelt regressor, trekker R regresjonslinjen automatisk!