katamorfismen for Enten er en generalisering av dens fold. Katamorfismen gjør at operasjoner ikke er tilgjengelige via fold.
denne artikkelen er en del av en artikkelserie om katamorfismer. En katamorfisme er en universell abstraksjon som beskriver hvordan man fordøyer en datastruktur til en potensielt mer kompakt verdi.
denne artikkelen presenterer katamorfismen For Enten (også Kjent Som Resultat), samt hvordan man identifiserer den. Begynnelsen av denne artikkelen presenterer katamorfismen I C#, med eksempler. Resten av artikkelen beskriver hvordan å utlede katamorfismen. Denne delen av artikkelen presenterer mitt arbeid I Haskell. Lesere som ikke er komfortable Med Haskell, kan bare lese den første delen, og vurdere resten av artikkelen som et valgfritt tillegg.
Enten Er en databeholder som modellerer to gjensidig eksklusive resultater. Det brukes ofte til å returnere verdier som kan være enten riktig (høyre) eller feil (venstre). I statisk skrevet funksjonell programmering med en preferanse for totale funksjoner, Enten tilbyr en saner, mer fornuftig måte å modellere suksess og feil resultater enn å kaste unntak.
C # catamorphism #
denne artikkelen bruker Kirken koding Av Enten. Katamorfismen for Enten er Match – metoden:
T Match<T>(Func<L, T> onLeft, Func<R, T> onRight);
Inntil denne artikkelen har alle tidligere katamorfismer vært et par laget av en startverdi og en funksjon. Enten katamorfisme er en generalisering, siden det er et par funksjoner. En funksjon håndterer saken der det er en venstre verdi, og den andre funksjonen håndterer saken der det er en riktig verdi. Begge funksjonene må returnere samme, samlende type, som ofte er en streng eller noe lignende som kan vises i et brukergrensesnitt:
> IEither<TimeSpan, int> e = new Left<TimeSpan, int>(TimeSpan.FromMinutes(3));> e.Match(ts => ts.ToString(), i => i.ToString())"00:03:00"> IEither<TimeSpan, int> e = new Right<TimeSpan, int>(42);> e.Match(ts => ts.ToString(), i => i.ToString())"42"
du vil ofte se eksempler som ovenfor som gjør både venstre og høyre tilfeller til strenger eller noe som kan representeres som en samlende responstype, men dette er på ingen måte nødvendig. Hvis du kan komme opp med en samlende type, kan du konvertere begge tilfeller til den typen:
> IEither<Guid, string> e = new Left<Guid, string>(Guid.NewGuid());> e.Match(g => g.ToString().Count(c => 'a' <= c), s => s.Length)12> IEither<Guid, string> e = new Right<Guid, string>("foo");> e.Match(g => g.ToString().Count(c => 'a' <= c), s => s.Length)3
i de to eksemplene ovenfor bruker du to forskjellige funksjoner som både reduserer henholdsvis Guid og string verdier til et tall. Funksjonen som gjør Guid verdier til et tall, teller hvor mange av de heksadesimale sifrene som er større Enn Eller lik A (10). Den andre funksjonen returnerer bare lengden på string, hvis den er der. Det eksemplet gir liten mening, men Match – metoden bryr seg ikke om det.
i praktisk bruk Brukes Enten Ofte til feilhåndtering. Artikkelen Om Kirken koding av enten inneholder et eksempel.
Enten F-Algebra #
som i forrige artikkel, bruker jeg Fix og cata som forklart I Bartosz Milewskis utmerkede artikkel Om F-Algebraer.
Mens F-Algebraer og faste punkter er mest brukt for rekursive datastrukturer, kan du også definere En F-Algebra for en ikke-rekursiv datastruktur. Du har allerede sett et eksempel på det i artiklene Om Boolsk katamorfisme og kanskje katamorfisme. Forskjellen mellom F. Eks. kanskje verdier og Enten er at begge tilfeller av enten har en verdi. Du kan modellere dette som en Functor med både en bærertype og to typeargumenter for dataene Som enten kan inneholde:
data EitherF l r c = LeftF l | RightF r deriving (Show, Eq, Read) instance Functor (EitherF l r) where fmap _ (LeftF l) = LeftF l fmap _ (RightF r) = RightF r
jeg valgte å ringe datatypene l (til venstre) og r (til høyre), og transportørtypen c (for transportør). Som det også var tilfelle med BoolF og MaybeF, ignorerer Functor – forekomsten kartfunksjonen fordi bærertypen mangler fra både LeftF – saken og RightF – saken. Som Functor – forekomstene for BoolF og MaybeF, ser det ut til at ingenting skjer, men på typenivå er dette fortsatt en oversettelse fra EitherF l r c til EitherF l r c1. Ikke mye av en funksjon, kanskje, men definitivt en endofunctor.
Som det også var tilfelle når man avledet Kanskje og Listekatamorfismer, Er Haskell ikke så glad for å definere forekomster for en type som Fix (EitherF l r). For å løse det problemet kan du introdusere en newtype wrapper:
newtype EitherFix l r = EitherFix { unEitherFix :: Fix (EitherF l r) } deriving (Show, Eq, Read)
Du kan definere Functor, Applicative, Monad, etc. forekomster for denne typen uten å ty til noen funky GHC utvidelser. Husk at i siste instans er formålet med all denne koden bare å finne ut hva katamorfismen ser ut. Denne koden er ikke ment for faktisk bruk.
et par hjelpefunksjoner gjør det enklere å definere EitherFix verdier:
leftF :: l -> EitherFix l rleftF = EitherFix . Fix . LeftF rightF :: r -> EitherFix l rrightF = EitherFix . Fix . RightF
med disse funksjonene kan du opprette EitherFix verdier:
Prelude Data.UUID Data.UUID.V4 Fix Either> leftF <$> nextRandomEitherFix {unEitherFix = Fix (LeftF e65378c2-0d6e-47e0-8bcb-7cc29d185fad)}Prelude Data.UUID Data.UUID.V4 Fix Either> rightF "foo"EitherFix {unEitherFix = Fix (RightF "foo")}
Det er alt du trenger for å identifisere katamorfismen.
Haskell catamorphism #
På dette punktet har du to av tre elementer I En F-Algebra. Du har en endofunctor (EitherF l r) og et objekt c, men du må fortsatt finne en morphism EitherF l r c -> c. Legg merke til at algebraen du må finne er funksjonen som reduserer funktoren til sin bærertype c, ikke datatypene l og r. Dette tar litt tid å bli vant til, men det er hvordan katamorfismer fungerer. Dette betyr imidlertid ikke at du kommer til å ignorere l og r, som du vil se.
som i de forrige artiklene, start med å skrive en funksjon som vil bli katamorfismen, basert på cata:
eitherF = cata alg . unEitherFix where alg (LeftF l) = undefined alg (RightF r) = undefined
Mens dette kompilerer, med sine undefined implementeringer, gjør det åpenbart ikke noe nyttig. Jeg finner imidlertid at det hjelper meg å tenke. Hvordan kan du returnere en verdi av typen c fra LeftF saken? Du kan sende et argument til eitherF – funksjonen:
eitherF fl = cata alg . unEitherFix where alg (LeftF l) = fl l alg (RightF r) = undefined
mens du teknisk sett kunne sende et argument av typen c til eitherF og deretter returnere den verdien fra LeftF – saken, ville det bety at du ville ignorere l – verdien. Dette ville være feil, så i stedet gjør argumentet en funksjon og ring det med l. På samme måte kan du håndtere RightF saken på samme måte:
eitherF :: (l -> c) -> (r -> c) -> EitherFix l r -> ceitherF fl fr = cata alg . unEitherFix where alg (LeftF l) = fl l alg (RightF r) = fr r
dette fungerer. Siden cata har typen Functor f => (f a -> a) -> Fix f -> a, betyr det at alg har typen f a -> a. I tilfelle EitherF konkluderer kompilatoren at funksjonen alg har typen EitherF l r c -> c, som er akkurat det du trenger!
Du kan nå se hva bærertypen c er for. Det er typen som algebra trekker ut, og dermed typen som katamorfismen returnerer.
Dette er da katamorfismen For Heller. Som det har vært konsistent så langt, er det et par, men nå laget av to funksjoner. Som du har sett gjentatte ganger, er dette ikke den eneste mulige katamorfismen, siden du for eksempel kan vende argumentene til eitherF.
jeg har valgt representasjonen vist her fordi den er isomorf til either – funksjonen fra Haskells innebygde Data.Either – modul, som kaller funksjonen «Case analysis for Either – typen». Begge disse funksjonene (eitherF og either) er ekvivalente med C# Match – metoden ovenfor.
Basis #
du kan implementere de fleste andre nyttige funksjoner med eitherF. Her er Bifunctor – forekomsten:
instance Bifunctor EitherFix where bimap f s = eitherF (leftF . f) (rightF . s)
fra den forekomsten følger Functor – forekomsten trivielt:
instance Functor (EitherFix l) where fmap = second
på toppen av Functor kan du legge til Applicative:
instance Applicative (EitherFix l) where pure = rightF f <*> x = eitherF leftF (<$> x) f
Legg Merke til at <*> – implementeringen ligner på <*> – implementeringen for MaybeFix. Det samme er tilfellet for Monad – forekomsten:
instance Monad (EitherFix l) where x >>= f = eitherF leftF f x
Ikke bare er EitherFix Foldable, det er Bifoldable:
instance Bifoldable EitherFix where bifoldMap = eitherF
Legg merke til at bifoldMap er identisk med eitherF.
Bifoldable – forekomsten lar deg trivielt implementere Foldable – forekomsten:
instance Foldable (EitherFix l) where foldMap = bifoldMap mempty
du kan finne tilstedeværelsen av mempty forvirrende, siden bifoldMap(eller eitherF; de er identiske) tar som argumenter to funksjoner. Er mempty en funksjon?
ja, mempty kan være en funksjon. Her er det. Det er en Monoid forekomst for enhver funksjon a -> m, der m er en Monoid forekomst, og mempty er identiteten for den monoiden. Det er tilfellet i bruk her.
Akkurat som EitherFix er Bifoldable, er det også Bitraversable:
instance Bitraversable EitherFix where bitraverse fl fr = eitherF (fmap leftF . fl) (fmap rightF . fr)
du kan komfortabelt implementere Traversable – forekomsten basert på Bitraversable – forekomsten:
instance Traversable (EitherFix l) where sequenceA = bisequenceA . first pure
Til slutt kan du implementere konverteringer til og fra standard Either – typen, ved hjelp av ana som dual of cata:
toEither :: EitherFix l r -> Either l rtoEither = eitherF Left Right fromEither :: Either a b -> EitherFix a bfromEither = EitherFix . ana coalg where coalg (Left l) = LeftF l coalg (Right r) = RightF r
Dette viser at EitherFix er isomorf til Either, som igjen fastslår at eitherF og either er ekvivalente.
Relasjoner #
i denne serien har du sett forskjellige eksempler på katamorfismer av strukturer som ikke har noen folder, katamorfismer som sammenfaller med folder, og nå en katamorfisme som er mer generell enn brettet. Introduksjonen til serien inkluderte dette diagrammet:
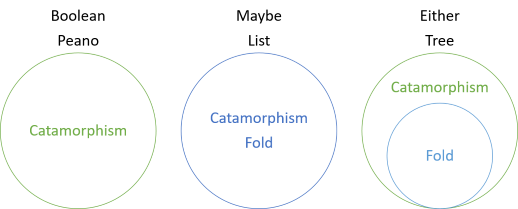
dette viser At Boolske verdier og Peano-tall har katamorfismer, men ingen folder, mens for Kanskje Og Liste er brettet og katamorfismen den samme. For Enten er folden et spesielt tilfelle av katamorfismen. Folden for enten ‘later’ at venstre side ikke eksisterer. I stedet tolkes den venstre verdien som en manglende riktig verdi. For å kaste begge verdiene må du derfor angi en reserveverdi som skal brukes hvis En Verdi Ikke er en riktig verdi:
Prelude Fix Either> e = rightF LT :: EitherFix Integer OrderingPrelude Fix Either> foldr (const . show) "" e"LT"Prelude Fix Either> e = leftF 42 :: EitherFix Integer OrderingPrelude Fix Either> foldr (const . show) "" e""
I En GHCi-økt som ovenfor kan du opprette To verdier Av samme type. Høyre tilfelle er en Ordering – verdi, mens venstre tilfelle er en Integer – verdi.
med foldr er det ingen måte å få tilgang til venstre tilfelle. Mens du kan få tilgang til og forvandle den riktige Ordering – verdien, blir tallet 42 bare ignorert under brettet. I stedet returneres standardverdien "".
Kontrast dette med katamorfismen, som kan få tilgang til begge tilfeller:
Prelude Fix Either> e = rightF LT :: EitherFix Integer OrderingPrelude Fix Either> eitherF show show e"LT"Prelude Fix Either> e = leftF 42 :: EitherFix Integer OrderingPrelude Fix Either> eitherF show show e"42"
I en økt som dette gjenskaper du de samme verdiene, men ved hjelp av katamorfismen eitherF kan du nå få tilgang til og transformere både venstre og høyre saker. Med andre ord gjør katamorfismen deg i stand til å utføre operasjoner som ikke er mulige med brettet.
det er imidlertid interessant å merke seg at mens brettet er en spesialisering av katamorfismen, er bifoldet identisk med katamorfismen.
Sammendrag #
katamorfismen for Begge er et par funksjoner. En funksjon forvandler venstre tilfelle, mens den andre funksjonen forvandler høyre tilfelle. For En hvilken som helst verdi, vil bare en av disse funksjonene bli brukt.
da jeg opprinnelig opplevde begrepet katamorfisme, fant jeg det vanskelig å skille mellom katamorfisme og brett. Mitt problem var, tror jeg, at tutorials jeg kjørte inn mest brukte koblede lister for å demonstrere hvordan, i så fall, fold er katamorfisme. Det viser seg imidlertid at dette ikke alltid er tilfelle. En katamorfisme er en generell abstraksjon. En fold, derimot, synes for meg å være mest relatert til samlinger.
i denne artikkelen så du det første eksempelet på en katamorfisme som kan gjøre mer enn folden. For enten er folden bare et spesielt tilfelle av katamorfismen. Du så også hvordan katamorfismen var identisk med bifold. Dermed er det fortsatt ikke helt klart hvordan disse konseptene relaterer seg. Derfor, i neste artikkel, får du et eksempel på en beholder der det ikke er bifold, og hvor katamorfismen faktisk er en generalisering av brettet.
Neste: tre katamorfisme.