Vurdering | Biopsykologi | Komparativ |Kognitiv | Utviklings | Språk | Individuelle forskjeller |Personlighet | Filosofi | Sosial |
Metoder | Statistikk |Klinisk | Pedagogisk | Industriell |Profesjonell elementer |Verdenspsykologi |
Statistikk:Vitenskapelig metode · forskningsmetoder · Eksperimentell design · Undergraduate statistikk kurs · Statistiske tester · Spillteori · Beslutningsteori
vennligst bidra til å forbedre denne siden selv hvis du kan..
Cluster analyse Eller clustering er en vanlig teknikk for statistisk dataanalyse, som brukes i mange felt, inkludert maskinlæring, data mining, mønstergjenkjenning, bildeanalyse og bioinformatikk. Clustering er klassifiseringen av lignende objekter i forskjellige grupper, eller mer presist, partisjonering av et datasett i delsett (klynger), slik at dataene i hvert delsett (ideelt) deler noe felles trekk-ofte nærhet i henhold til noen definert avstandsmål.
I Tillegg til begrepet data clustering (eller bare clustering), er det en rekke begreper med lignende betydninger, inkludert klyngeanalyse, automatisk klassifisering, numerisk taksonomi, botryologi og typologisk analyse.
- typer clustering
- Hierarkisk clustering
- Avstandsmål
- Opprette klynger
- Agglomerativ hierarkisk gruppering
- Partitional clustering
- k-betyr og derivater
- K – betyr clustering
- QT Clust algoritme
- Fuzzy c-betyr clustering
- Albuekriterium
- Spektral clustering
- Applikasjoner
- Biologi
- markedsundersøkelser
- Andre applikasjoner
- Sammenligninger mellom dataklusteringer
- Se også
- Bibliografi
- programvareimplementeringer
- Gratis
typer clustering
data clustering algoritmer kan være hierarkisk eller partisjonell. Hierarkiske algoritmer finner suksessive klynger ved hjelp av tidligere etablerte klynger, mens partisjonsalgoritmer bestemmer alle klynger samtidig. Hierarkiske algoritmer kan være agglomerative (bottom-up) eller splittende (top-down). Agglomerative algoritmer begynner med hvert element som en egen klynge og fusjonerer dem i suksessivt større klynger. Splittende algoritmer begynner med hele settet og fortsetter å dele det i suksessivt mindre klynger.
Hierarkisk clustering
Avstandsmål
et viktig trinn i en hierarkisk clustering er å velge et avstandsmål. Et enkelt mål er manhattan avstand, lik summen av absolutte avstander for hver variabel. Navnet kommer fra det faktum at i et to-variabelt tilfelle kan variablene plottes på et rutenett som kan sammenlignes med bygater, og avstanden mellom to punkter er antall blokker en person vil gå.
Et mer vanlig mål Er Euklidisk avstand, beregnet ved å finne kvadratet av avstanden mellom hver variabel, summere kvadratene og finne kvadratroten av den summen. I det to-variable tilfellet er avstanden analog med å finne lengden på hypotenusen i en trekant; det vil si at det er avstanden » i luftlinje.»En gjennomgang av klyngeanalyse i helsepsykologiforskning fant at det vanligste avstandsmålet i publiserte studier i det forskningsområdet er Euklidisk avstand eller den kvadrerte Euklidiske avstanden.
Opprette klynger
gitt et avstandsmål kan elementer kombineres. Hierarkisk clustering bygger (agglomerativ), eller bryter opp (splittende), et hierarki av klynger. Den tradisjonelle representasjonen av dette hierarkiet er en trestruktur (kalt et dendrogram), med individuelle elementer i den ene enden og en enkelt klynge med hvert element i den andre. Agglomerative algoritmer begynner på toppen av treet, mens splittende algoritmer begynner på bunnen. (I figuren indikerer pilene en agglomerativ clustering.)
Kutting av treet i en gitt høyde vil gi en clustering med en valgt presisjon. I følgende eksempel vil kutting etter den andre raden gi klynger {a} {b c} {d e} {f}. Kutting etter tredje rad vil gi klynger {a} {b c} {d e f}, som er en grovere clustering, med færre antall større klynger.
Agglomerativ hierarkisk gruppering
anta for eksempel at disse dataene skal grupperes. Hvor euklidsk avstand er avstanden metrisk.
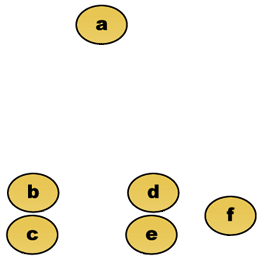
Rådata
det hierarkiske clustering dendrogrammet ville være som sådan:
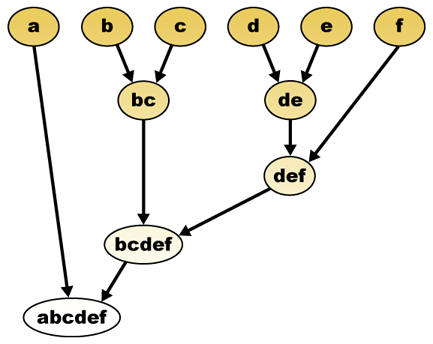
Tradisjonell representasjon
denne metoden bygger hierarkiet fra de enkelte elementene ved gradvis sammenslåing av klynger. Igjen har vi seks elementer {a} {b} {c} {d} {e} og {f}. Det første trinnet er å bestemme hvilke elementer som skal slås sammen i en klynge. Vanligvis vil vi ta de to nærmeste elementene, derfor må vi definere en avstand 
Anta at vi har slått sammen de to nærmeste elementene b og c, vi har nå følgende klynger {a}, {b, c}, {d}, {e} og {f}, Og vil slå dem sammen videre. Men for å gjøre det må vi ta avstanden mellom {a} og {b c}, og derfor definere avstanden mellom to klynger. Vanligvis er avstanden mellom to klynger 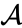
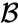
- maksimal avstand mellom elementene i hver klynge (også kalt komplett kobling clustering):
- minste avstand mellom elementene i hver klynge (også kalt single linkage clustering):
- gjennomsnittlig avstand mellom elementene i hver klynge (også kalt gjennomsnittlig kobling clustering):
- summen av alle intra-klynge varians
- økningen i varians for klyngen som flettes (Ward kriterium)
- sannsynligheten for at kandidatklynger gyter fra samme distribusjonsfunksjon (V-kobling)
Hver agglomerasjon skjer i større avstand mellom klynger enn den forrige agglomerasjonen, og man kan bestemme seg for å stoppe clustering enten når klyngene er for langt fra hverandre til å flettes (avstandskriterium) eller når det er et tilstrekkelig lite antall klynger (tallkriterium).
Partitional clustering
k-betyr og derivater
K – betyr clustering
k-betyr algoritmen tilordner hvert punkt til klyngen hvis senter (også kalt centroid) er nærmest. Senteret er gjennomsnittet av alle punktene i klyngen — det vil si at koordinatene er det aritmetiske gjennomsnittet for hver dimensjon separat over alle punktene i klyngen.
Eksempel: Datasettet har tre dimensjoner og klyngen har to punkter: X = (x1, x2, x3) Og Y = (y1, y2, y3). Deretter blir centroid Z Z = (z1, z2, z3), hvor z1 = (x1 + y1)/2 og z2 = (x2 + y2)/2 og z3 = (x3 + y3) / 2.
algoritmen er omtrent (J. MacQueen, 1967):
- Tilfeldig generere k klynger og bestemme klyngen sentre, eller direkte generere k frø poeng som klyngen sentre.
- Tilordne hvert punkt til nærmeste klyngesenter.
- Rekomputer de nye klyngesentrene.
- Gjenta til noe konvergenskriterium er oppfylt(vanligvis at tildelingen ikke er endret).
de viktigste fordelene med denne algoritmen er dens enkelhet og hastighet som gjør det mulig å kjøre på store datasett. Ulempen er at den ikke gir det samme resultatet med hvert løp, siden de resulterende klyngene er avhengige av de første tilfeldige oppdragene. Det maksimerer inter-cluster (eller minimerer intra-cluster) varians, men sikrer ikke at resultatet har et globalt minimum av varians.
QT Clust algoritme
QT (Kvalitet Terskel) Clustering (Heyer et al, 1999) er en alternativ metode for partisjonering data, oppfunnet for genet clustering. Det krever mer datakraft enn k-midler, men krever ikke å spesifisere antall klynger a priori, og returnerer alltid det samme resultatet når det kjøres flere ganger.
algoritmen er:
- brukeren velger en maksimal diameter for klynger.
- Bygg en kandidatklynge for hvert punkt ved å inkludere nærmeste punkt, neste nærmeste og så videre, til diameteren til klyngen overgår terskelen.
- Lagre kandidatklyngen med flest poeng som den første sanne klyngen, og fjern alle punktene i klyngen fra videre vurdering.
- Recurse med det reduserte settet med poeng.
avstanden mellom et punkt og en gruppe punkter beregnes ved hjelp av fullstendig kobling, dvs. som maksimal avstand fra punktet til et medlem av gruppen (se delen «Agglomerativ hierarkisk clustering» om avstand mellom klynger).
Fuzzy c-betyr clustering
i fuzzy clustering har hvert punkt en grad av tilhørighet til klynger, som i fuzzy logic, i stedet for å tilhøre helt til bare en klynge. Dermed kan punkter på kanten av en klynge, være i klyngen i mindre grad enn punkter i sentrum av klyngen. For hvert punkt x har vi en koeffisient som gir graden av å være i kth-klyngen 

med fuzzy c-midler er centroid av en klynge gjennomsnittet av alle punkter, vektet av deres grad av tilhørighet til klyngen:
graden av tilhørighet er relatert til den inverse av avstanden til klyngen
deretter normaliseres koeffisientene og fuzzyfiseres med en reell parameter 
for m lik 2, tilsvarer dette å normalisere koeffisienten lineært for å gjøre summen 1. Når m er nær 1, blir klyngesenteret nærmest punktet gitt mye mer vekt enn de andre, og algoritmen ligner k-midler.
fuzzy c-means-algoritmen er veldig lik k-means-algoritmen:
- Velg et antall klynger.
- Tilordne tilfeldig til hver punktkoeffisient for å være i klyngene.
- Gjenta til algoritmen har konvergert (det vil si at koeffisientenes endring mellom to iterasjoner ikke er mer enn
, den gitte følsomhetsgrensen) :
- Beregn centroid for hver klynge, ved hjelp av formelen ovenfor.
- for hvert punkt beregner du koeffisientene for å være i klyngene, ved hjelp av formelen ovenfor.
algoritmen minimerer også intra-cluster varians, men har de samme problemene som k-midler, minimumet er et lokalt minimum, og resultatene avhenger av det første valget av vekter.
Albuekriterium
albuekriteriet er en vanlig tommelfingerregel for å bestemme hvilket antall klynger som skal velges, for eksempel for k-midler og agglomerativ hierarkisk clustering.
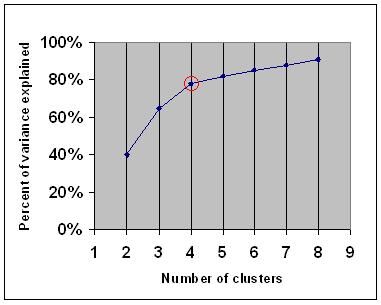
elbow-kriteriet sier at du bør velge et antall klynger slik at det ikke legges til nok informasjon ved å legge til en annen klynge. Nærmere bestemt, hvis du grafer prosentandelen av variansen forklart av klyngene mot antall klynger, vil de første klyngene legge til mye informasjon (forklare mye varians), men på et tidspunkt vil den marginale gevinsten falle, noe som gir en vinkel i grafen (albuen).
på følgende graf er albuen angitt med den røde sirkelen. Antall valgte klynger bør derfor være 4.
Spektral clustering
gitt et sett med datapunkter, kan likhetsmatrisen defineres som en matrise 


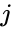
En slik teknikk Er shi-Malik-algoritmen, som vanligvis brukes til bildesegmentering. Den partisjoner peker i to sett 

av 
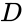
denne partisjoneringen kan gjøres på forskjellige måter, for eksempel ved å ta medianen 



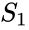
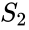
en relatert algoritme er meila-shi-algoritmen, som tar egenvektorene som svarer til de k største egenverdiene av matrisen 
Applikasjoner
Biologi
i biologi clustering har mange applikasjoner innen beregningsbiologi og bioinformatikk, hvorav to er:
- i transkriptomikk brukes clustering til å bygge grupper av gener med relaterte uttrykksmønstre. Ofte inneholder slike grupper funksjonelt relaterte proteiner, for eksempel enzymer for en bestemt vei, eller gener som er samregulert. Høy gjennomstrømmingsforsøk ved hjelp av uttrykte sekvensmerker (ESTs) eller DNA-mikroarrays kan være et kraftig verktøy for genomannotasjon, et generelt aspekt av genomikk.
- i sekvensanalyse brukes clustering til å gruppere homologe sekvenser i genfamilier. Dette er et svært viktig konsept innen bioinformatikk, og evolusjonsbiologi generelt. Se evolusjon ved gen duplisering.
markedsundersøkelser
Klyngeanalyse er mye brukt i markedsundersøkelser når man arbeider med multivariate data fra undersøkelser og testpaneler. Markedsforskere bruker klyngeanalyse for å dele den generelle befolkningen av forbrukere inn i markedssegmenter og for bedre å forstå forholdet mellom ulike grupper av forbrukere / potensielle kunder.
- Segmentere markedet og bestemme målmarkeder
- produktposisjonering
- utvikling Av nye produkter
- Velge testmarkeder (se : eksperimentelle teknikker)
Andre applikasjoner
Sosial nettverksanalyse: i studiet av sosiale nettverk kan clustering brukes til å gjenkjenne samfunn innenfor store grupper av mennesker.
Bildesegmentering: Clustering kan brukes til å dele et digitalt bilde i forskjellige områder for grensegjenkjenning eller objektgjenkjenning.
data mining: Mange data mining applikasjoner involverer partisjonering av dataelementer i relaterte undergrupper; markedsføringsapplikasjonene diskutert ovenfor representerer noen eksempler. En annen vanlig søknad er oppdeling av dokumenter, for Eksempel World Wide Web-sider, i sjangere.
Sammenligninger mellom dataklusteringer
det har vært flere forslag til et mål på likhet mellom to klynger. Et slikt tiltak kan brukes til å sammenligne hvor godt forskjellige data clustering algoritmer utføre på et sett av data. Mange av disse tiltakene er avledet fra samsvarende matrise (aka forvirring matrise), f. eks Rand tiltaket Og fowlkes-Mallows Bk tiltak.
- Jain, Murty Og Flynn: Data Clustering: En Gjennomgang, ACM Comp. Surv., 1999. Tilgjengelig her.
- for en annen presentasjon av hierarkiske, k-midler og fuzzy c-midler, se denne introduksjonen til clustering. Har også en forklaring på blanding Av Gaussere.
- David Dowe, Blanding Modellering side-andre clustering og blanding modell lenker.
- en tutorial på clustering
- on-line lærebok: Informasjonsteori, Slutning, Og Læring Algoritmer, Av David Jc MacKay inneholder kapitler om k-betyr clustering, myk k-betyr clustering, og avledninger inkludert E-M algoritmen og variational visning Av E-M algoritmen.
Se også
- k-betyr
- Kunstig nevralt nettverk (ANN)
- selvorganiserende kart
- Forventningsmaksimering (EM)
Bibliografi
- Clatworthy, J., Buick, D., Hankins, M., Weinman, J., & Horne, R. (2005). Bruk og rapportering av klyngeanalyse i helsepsykologi: en gjennomgang. British Journal Of Health Psychology 10: 329-358.
- Romesburg, H. Clarles, Klyngeanalyse For Forskere, 2004, 340 pp. ISBN 1411606175 eller utgiver, opptrykk av 1990-utgaven utgitt Av Krieger Pub. Medeier… En Japansk oversettelse er tilgjengelig Fra Uchida Rokakuho Publishing Co., Ltd., Tokyo, Japan.
- Heyer, Lj, Kruglyak, S. Og Yooseph, S., Utforske Uttrykksdata: Identifikasjon Og Analyse Av Coexpressed Gener, Genome Research 9:1106-1115.
- den elektroniske læreboken: Informasjonsteori, Inferens og Læringsalgoritmer, Av David Jc MacKay inneholder kapitler om k – betyr clustering, myk k – betyr clustering og avledninger, inkludert e-m-algoritmen og variasjonsvisningen Av e-m-algoritmen.
for spektral clustering :
- Jianbo Shi Og Jitendra Malik, «Normaliserte Kutt og Bildesegmentering», Ieee-Transaksjoner På Mønsteranalyse og Maskinintelligens, 22(8), 888-905, August 2000. Tilgjengelig på jitendra Maliks hjemmeside
- Marina Meila Og Jianbo Shi, «Learning Segmentation with Random Walk», Neural Information Processing Systems, NIPS, 2001. Tilgjengelig fra Jianbo Shis hjemmeside
for å estimere antall klynger:
- Kan, F., Ozkarahan, E. A. (1990) » Begreper og effektivitet av coveret koeffisientbasert clustering metodikk for tekstdatabaser.»ACM Transaksjoner På Databasesystemer. 15 (4) 483-517.
programvareimplementeringer
Gratis
- flexclust-pakken FOR R
- YALE (Enda Et Læringsmiljø): gratis åpen kildekode – programvare for kunnskapsoppdagelse og datautvinning inkluderer også en plugin for klynging
- Noen Matlab kildefiler for klynging her
- kompakt-komparativ pakke for klyngevurdering (også i matlab)
- mixmod : Modellbasert Klynge-Og Diskriminantanalyse. Kode I c++, grensesnitt Med Matlab Og Scilab
- LingPipe Clustering Tutorial Tutorial for å gjøre komplett-og single-link clustering bruker LingPipe, En Java tekst data mining pakke distribuert med kilde.
- Weka : Weka inneholder verktøy for databehandling, klassifisering, regresjon, clustering, assosiasjonsregler og visualisering. Det er også godt egnet for utvikling av nye maskinlæringsordninger.