Ifølge Noam Chomosky er det fire typer grammatikker − type 0, Type 1, type 2 Og type 3. Tabellen nedenfor viser hvordan de skiller seg fra hverandre−
| Grammatikk Type | Grammatikk Akseptert | Språk Akseptert | Automat |
|---|---|---|---|
| Skriv 0 | Ubegrenset grammatikk | Rekursivt enumerable språk | Turing Machine |
| Type 1 | Kontekstavhengig grammatikk | Kontekstavhengig språk | Lineær-avgrenset automat |
| Skriv Inn 2 | Kontekstfri grammatikk | Kontekstfritt språk | Pushdown automat |
| Skriv 3 | Vanlig grammatikk | Vanlig språk | Endelig tilstandsautomat |
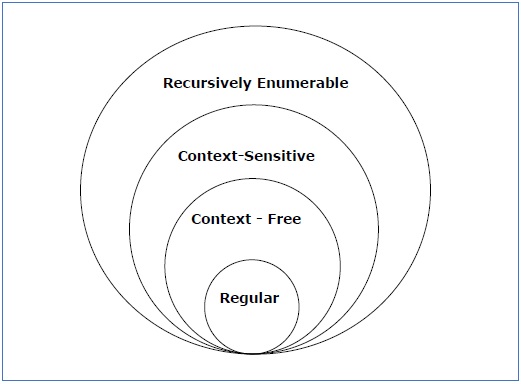
Ta en titt på følgende illustrasjon. Det viser omfanget av hver type grammatikk –
Type-3 Grammatikk
Type-3 grammatikker genererer vanlige språk. Type-3 grammatikker må ha en enkelt ikke-terminal på venstre side og en høyre side bestående av en enkelt terminal eller en enkelt terminal etterfulgt av en enkelt ikke-terminal.
produktioner må være I form X → a eller X → ay
Hvor X, Y ∈ N (Ikke terminal)
og en ∈ t (Terminal)
regelen s → ε er tillatt hvis s ikke vises på høyre side av en regel.
Eksempel
X → ε X → a | aYY → b
Type-2 Grammatikk
Type – 2 grammatikker genererer kontekstfrie språk.
produksjonene må være i form av en → γ
Der En ∈ N (Ikke Terminal)
og γ ∈ (t ∪ N) * (Rekke Terminaler og Ikke-terminaler).
disse språkene som genereres av disse grammatikkene, gjenkjennes av en ikke-deterministisk pushdown-automat.
Eksempel
S → X a X → a X → aX X → abc X → ε
Type-1 Grammatikk
Type-1 grammatikk genererer kontekstavhengige språk. Produksjoner må være i form
α A β → α γ β
hvor A ∈ N (Ikke-terminal)
og α, β, γ ∈ (T ∪ N)* (Strenger av terminaler og ikke-terminaler)
strengene α og β kan være tom, men γ må være ikke-tom.
regelen s → ε er tillatt hvis s ikke vises på høyre side av noen regel. Språkene som genereres av disse grammatikkene, gjenkjennes av en lineær begrenset automat.
Eksempel
AB → AbBc A → bcA B → b
Type-0 Grammatikk
Type – 0 grammatikker genererer rekursivt nummererbare språk. Produksjonene har ingen begrensninger. De er noen fase struktur grammatikk inkludert alle formelle grammatikker.
de genererer språkene som gjenkjennes av En Turing-maskin.
produktioner kan være i form av α → β der α er en rekke terminaler og ikke-terminaler med minst en ikke-terminal og α ikke kan være null. β er en rekke terminaler og ikke-terminaler.
Eksempel
S → ACaB Bc → acB CB → DB aD → Db