Le catamorphisme pour L’Un ou l’autre est une généralisation de son pli. Le catamorphisme permet des opérations non disponibles via le pliage.
Cet article fait partie d’une série d’articles sur les catamorphismes. Un catamorphisme est une abstraction universelle qui décrit comment digérer une structure de données en une valeur potentiellement plus compacte.
Cet article présente le catamorphisme pour l’Un ou l’autre (également appelé Résultat), ainsi que la façon de l’identifier. Le début de cet article présente le catamorphisme en C#, avec des exemples. Le reste de l’article décrit comment déduire le catamorphisme. Cette partie de l’article présente mon travail à Haskell. Les lecteurs qui ne sont pas à l’aise avec Haskell peuvent simplement lire la première partie et considérer le reste de l’article comme une annexe facultative.
L’un ou l’autre est un conteneur de données qui modèle deux résultats mutuellement exclusifs. Il est souvent utilisé pour renvoyer des valeurs qui peuvent être correctes (à droite) ou incorrectes (à gauche). Dans la programmation fonctionnelle typée statiquement avec une préférence pour les fonctions totales, l’une ou l’autre offre un moyen plus sain et plus raisonnable de modéliser les résultats de réussite et d’erreur que de lancer des exceptions.
C#catamorphism#
Cet article utilise le codage Church de l’un ou l’autre. Le catamorphisme pour l’un ou l’autre est la méthode Match:
T Match<T>(Func<L, T> onLeft, Func<R, T> onRight);
Jusqu’à cet article, tous les catamorphismes précédents étaient une paire faite à partir d’une valeur initiale et d’une fonction. L’un ou l’autre catamorphisme est une généralisation, car c’est une paire de fonctions. Une fonction gère le cas où il y a une valeur de gauche, et l’autre fonction gère le cas où il y a une valeur de droite. Les deux fonctions doivent renvoyer le même type unificateur, qui est souvent une chaîne ou quelque chose de similaire pouvant être affiché dans une interface utilisateur:
> IEither<TimeSpan, int> e = new Left<TimeSpan, int>(TimeSpan.FromMinutes(3));> e.Match(ts => ts.ToString(), i => i.ToString())"00:03:00"> IEither<TimeSpan, int> e = new Right<TimeSpan, int>(42);> e.Match(ts => ts.ToString(), i => i.ToString())"42"
Vous verrez souvent des exemples comme ceux ci-dessus qui transforment les cas gauche et droit en chaînes ou quelque chose qui peut être représenté comme un type de réponse unificateur, mais cela n’est en aucun cas nécessaire. Si vous pouvez trouver un type unificateur, vous pouvez convertir les deux cas en ce type:
> IEither<Guid, string> e = new Left<Guid, string>(Guid.NewGuid());> e.Match(g => g.ToString().Count(c => 'a' <= c), s => s.Length)12> IEither<Guid, string> e = new Right<Guid, string>("foo");> e.Match(g => g.ToString().Count(c => 'a' <= c), s => s.Length)3
Dans les deux exemples ci-dessus, vous utilisez deux fonctions différentes qui réduisent respectivement les valeurs Guid et string à un nombre. La fonction qui transforme les valeurs Guid en un nombre compte le nombre de chiffres hexadécimaux supérieurs ou égaux à A(10). L’autre fonction renvoie simplement la longueur de string, si elle est là. Cet exemple a peu de sens, mais la méthode Match ne s’en soucie pas.
En pratique, l’un ou l’autre est souvent utilisé pour la gestion des erreurs. L’article sur l’encodage de l’Église de l’un ou l’autre contient un exemple.
Soit F-Algèbre #
Comme dans l’article précédent, j’utiliserai Fix et cata comme expliqué dans l’excellent article de Bartosz Milewski sur les F-algèbres.
Bien que les algèbres F et les points fixes soient principalement utilisés pour les structures de données récursives, vous pouvez également définir une algèbre F pour une structure de données non récursive. Vous en avez déjà vu un exemple dans les articles sur le catamorphisme booléen et peut-être le catamorphisme. La différence entre, par exemple, Peut-être des valeurs et l’Une ou l’autre est que les deux cas de l’une ou l’autre portent une valeur. Vous pouvez modéliser cela en tant que Functor avec à la fois un type de porteuse et deux arguments de type pour les données qui peuvent contenir:
data EitherF l r c = LeftF l | RightF r deriving (Show, Eq, Read) instance Functor (EitherF l r) where fmap _ (LeftF l) = LeftF l fmap _ (RightF r) = RightF r
J’ai choisi d’appeler les ‘types de données’ l (pour la gauche) et r (pour la droite), et le type de porteuse c (pour la porteuse). Comme c’était également le cas avec BoolF et MaybeF, l’instance Functor ignore la fonction map car le type de porteuse est absent à la fois du cas LeftF et du cas RightF. Comme les instances Functor pour BoolF et MaybeF, il semblerait que rien ne se passe, mais au niveau du type, il s’agit toujours d’une traduction de EitherF l r c à EitherF l r c1. Pas beaucoup d’une fonction, peut-être, mais certainement un endofunctor.
Comme c’était également le cas lors de la déduction des catamorphismes Maybe et List, Haskell n’est pas trop content de définir des instances pour un type comme Fix (EitherF l r). Pour résoudre ce problème, vous pouvez introduire un wrapper newtype:
newtype EitherFix l r = EitherFix { unEitherFix :: Fix (EitherF l r) } deriving (Show, Eq, Read)
Vous pouvez définir Functor, Applicative, Monad, etc. instances pour ce type sans avoir recours à des extensions GHC géniales. Gardez à l’esprit qu’en fin de compte, le but de tout ce code est simplement de comprendre à quoi ressemble le catamorphisme. Ce code n’est pas destiné à une utilisation réelle.
Une paire de fonctions auxiliaires facilite la définition des valeurs EitherFix:
leftF :: l -> EitherFix l rleftF = EitherFix . Fix . LeftF rightF :: r -> EitherFix l rrightF = EitherFix . Fix . RightF
Avec ces fonctions, vous pouvez créer des valeurs EitherFix:
Prelude Data.UUID Data.UUID.V4 Fix Either> leftF <$> nextRandomEitherFix {unEitherFix = Fix (LeftF e65378c2-0d6e-47e0-8bcb-7cc29d185fad)}Prelude Data.UUID Data.UUID.V4 Fix Either> rightF "foo"EitherFix {unEitherFix = Fix (RightF "foo")}
C’est tout ce dont vous avez besoin pour identifier le catamorphisme.
Catamorphisme de Haskell #
À ce stade, vous avez deux des trois éléments d’une F-Algèbre. Vous avez un endofunctor (EitherF l r) et un objet c, mais vous devez toujours trouver un morphisme EitherF l r c -> c. Notez que l’algèbre que vous devez trouver est la fonction qui réduit le foncteur à son type de porteuse c, pas les « types de données » l et r. Cela prend un certain temps pour s’y habituer, mais c’est ainsi que fonctionnent les catamorphismes. Cela ne signifie cependant pas que vous devez ignorer l et r, comme vous le verrez.
Comme dans les articles précédents, commencez par écrire une fonction qui deviendra le catamorphisme, basée sur cata:
eitherF = cata alg . unEitherFix where alg (LeftF l) = undefined alg (RightF r) = undefined
Bien que cela compile, avec ses implémentations undefined, cela ne fait évidemment rien d’utile. Je trouve cependant que cela m’aide à réfléchir. Comment pouvez-vous renvoyer une valeur du type c à partir du cas LeftF? Vous pouvez passer un argument à la fonction eitherF:
eitherF fl = cata alg . unEitherFix where alg (LeftF l) = fl l alg (RightF r) = undefined
Bien que vous puissiez techniquement passer un argument du type c à eitherF, puis renvoyer cette valeur à partir du cas LeftF, cela signifierait que vous ignoreriez la valeur l. Ce serait incorrect, alors faites plutôt de l’argument une fonction et appelez-le avec l. De même, vous pouvez traiter le cas RightF de la même manière:
eitherF :: (l -> c) -> (r -> c) -> EitherFix l r -> ceitherF fl fr = cata alg . unEitherFix where alg (LeftF l) = fl l alg (RightF r) = fr r
Ça marche. Puisque cata a le type Functor f => (f a -> a) -> Fix f -> a, cela signifie que alg a le type f a -> a. Dans le cas de EitherF, le compilateur en déduit que la fonction alg a le type EitherF l r c -> c, ce qui est exactement ce dont vous avez besoin!
Vous pouvez maintenant voir à quoi sert le type de transporteur c. C’est le type que l’algèbre extrait, et donc le type que le catamorphisme renvoie.
C’est donc le catamorphisme pour l’un ou l’autre. Comme cela a été cohérent jusqu’à présent, c’est une paire, mais maintenant composée de deux fonctions. Comme vous l’avez vu à plusieurs reprises, ce n’est pas le seul catamorphisme possible, car vous pouvez, par exemple, retourner trivialement les arguments à eitherF.
J’ai choisi la représentation affichée ici car elle est isomorphe à la fonction either du module Data.Either intégré de Haskell, qui appelle la fonction « Analyse de cas pour le type Either« . Ces deux fonctions (eitherF et either) sont équivalentes à la méthode C# Match ci-dessus.
Base #
Vous pouvez implémenter la plupart des autres fonctionnalités utiles avec eitherF. Voici l’instance Bifunctor:
instance Bifunctor EitherFix where bimap f s = eitherF (leftF . f) (rightF . s)
À partir de cette instance, l’instance Functor suit trivialement:
instance Functor (EitherFix l) where fmap = second
En plus de Functor, vous pouvez ajouter Applicative:
instance Applicative (EitherFix l) where pure = rightF f <*> x = eitherF leftF (<$> x) f
Notez que l’implémentation <*> est similaire à l’implémentation <*> pour MaybeFix. Il en est de même pour l’instance Monad:
instance Monad (EitherFix l) where x >>= f = eitherF leftF f x
Non seulement EitherFix Foldable, c’est Bifoldable:
instance Bifoldable EitherFix where bifoldMap = eitherF
Notez, de manière intéressante, que bifoldMap est identique à eitherF.
L’instance Bifoldable vous permet d’implémenter trivialement l’instance Foldable:
instance Foldable (EitherFix l) where foldMap = bifoldMap mempty
Vous pouvez trouver la présence de mempty déroutante, car bifoldMap (ou eitherF; ils sont identiques) prend comme arguments deux fonctions. mempty est-il une fonction ?
Oui, mempty peut être une fonction. Voilà, ça l’est. Il existe une instance Monoid pour toute fonction a -> m, où m est une instance Monoid et mempty est l’identité de ce monoïde. C’est l’instance utilisée ici.
Tout comme EitherFix est Bifoldable, c’est aussi Bitraversable:
instance Bitraversable EitherFix where bitraverse fl fr = eitherF (fmap leftF . fl) (fmap rightF . fr)
Vous pouvez facilement implémenter l’instance Traversable basée sur l’instance Bitraversable:
instance Traversable (EitherFix l) where sequenceA = bisequenceA . first pure
Enfin, vous pouvez implémenter des conversions vers et depuis le type Either standard, en utilisant ana comme dual de cata:
toEither :: EitherFix l r -> Either l rtoEither = eitherF Left Right fromEither :: Either a b -> EitherFix a bfromEither = EitherFix . ana coalg where coalg (Left l) = LeftF l coalg (Right r) = RightF r
Ceci démontre que EitherFix est isomorphe à Either, ce qui établit à nouveau que eitherF et either sont équivalents.
Relations #
Dans cette série, vous avez vu divers exemples de catamorphismes de structures qui n’ont pas de plis, des catamorphismes qui coïncident avec des plis, et maintenant un catamorphisme plus général que le pli. L’introduction à la série comprenait ce diagramme:
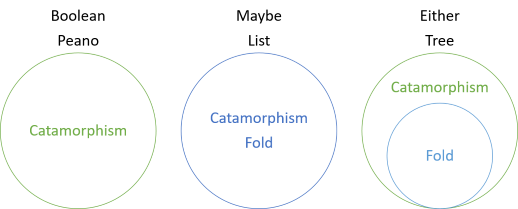
Cela montre que les valeurs booléennes et les nombres de Peano ont des catamorphismes, mais pas de plis, alors que pour Maybe et List, le pli et le catamorphisme sont les mêmes. Pour l’un ou l’autre, cependant, le pli est un cas particulier du catamorphisme. Le pli pour l’un ou l’autre « prétend » que le côté gauche n’existe pas. Au lieu de cela, la valeur de gauche est interprétée comme une valeur de droite manquante. Ainsi, pour plier l’une ou l’autre des valeurs, vous devez fournir une valeur de « repli » qui sera utilisée au cas où l’une ou l’autre des valeurs ne serait pas une bonne valeur:
Prelude Fix Either> e = rightF LT :: EitherFix Integer OrderingPrelude Fix Either> foldr (const . show) "" e"LT"Prelude Fix Either> e = leftF 42 :: EitherFix Integer OrderingPrelude Fix Either> foldr (const . show) "" e""
Dans une session GHCi comme ci-dessus, vous pouvez créer deux valeurs du même type. La casse de droite est une valeur Ordering, tandis que la casse de gauche est une valeur Integer.
Avec foldr, il n’y a aucun moyen d’accéder au boîtier de gauche. Bien que vous puissiez accéder et transformer la bonne valeur Ordering, le nombre 42 est simplement ignoré pendant le pliage. Au lieu de cela, la valeur par défaut "" est renvoyée.
Contraste avec le catamorphisme, qui peut accéder aux deux cas:
Prelude Fix Either> e = rightF LT :: EitherFix Integer OrderingPrelude Fix Either> eitherF show show e"LT"Prelude Fix Either> e = leftF 42 :: EitherFix Integer OrderingPrelude Fix Either> eitherF show show e"42"
Dans une session comme celle-ci, vous recréez les mêmes valeurs, mais en utilisant le catamorphisme eitherF, vous pouvez maintenant accéder et transformer les cas gauche et droit. En d’autres termes, le catamorphisme permet d’effectuer des opérations impossibles avec le pli.
Il est cependant intéressant de noter que si le pli est une spécialisation du catamorphisme, le pli est identique au catamorphisme.
Résumé #
Le catamorphisme pour l’une ou l’autre est une paire de fonctions. Une fonction transforme le boîtier gauche, tandis que l’autre fonction transforme le boîtier droit. Pour n’importe quelle valeur, une seule de ces fonctions sera utilisée.
Lorsque j’ai rencontré à l’origine le concept de catamorphisme, j’ai eu du mal à faire la distinction entre catamorphisme et pli. Mon problème était, je pense, que les tutoriels que j’ai rencontrés utilisaient principalement des listes chaînées pour démontrer comment, dans ce cas, le pli est le catamorphisme. Il s’avère cependant que ce n’est pas toujours le cas. Un catamorphisme est une abstraction générale. Un pli, en revanche, me semble être principalement lié aux collections.
Dans cet article, vous avez vu le premier exemple d’un catamorphisme qui peut faire plus que le pli. Pour l’un ou l’autre, le pli n’est qu’un cas particulier du catamorphisme. Vous avez également vu, cependant, comment le catamorphisme était identique au bifold. Ainsi, il n’est toujours pas tout à fait clair comment ces concepts se rapportent. Par conséquent, dans le prochain article, vous obtiendrez un exemple de conteneur où il n’y a pas de pli, et où le catamorphisme est, en effet, une généralisation du pli.
Suivant : Catamorphisme des arbres.