Algorithme:
Techniquement, l’ensemble d’instructions ou de description dans une notation particulière du processus est appelé algorithme. Un algorithme est une instruction finie étape par étape bien définie de la séquence des activités qui constituent un processus d’obtention des sorties souhaitées à partir des entrées données. La matière première nécessaire au moment du début est appelée entrée et l’entité rouillée est appelée sortie.
Caractéristiques d’un algorithme:
Il existe cinq caractéristiques importantes d’un algorithme qui doivent être prises en compte lors de la conception d’un algorithme pour tout problème.
Finesse: Un algorithme doit terminer un nombre infini d’étapes et chaque étape doit se terminer en un temps fini.
Lire Aussi | Doit Lire des Livres pour les Ingénieurs logiciels – Meilleur développeur
Définition (Pas d’ambiguïté): Chaque étape de l’algorithme doit être clairement et précisément définie et il ne doit pas y avoir d’ambiguïté. Exemple: Un fragment de programme est donné comme suit: x ← 1, lancez une pièce, si le résultat est head alors x← 3 sinon x ← 4. Dans le programme ci-dessus, toutes les étapes seraient effectuées efficacement mais il n’y a pas de définition car il y a deux valeurs possibles de x c’est-à-dire 1 et 3/4
Entrées: Un algorithme doit avoir zéro ou plus mais doit avoir un nombre fini d’entrées. Exemple d’algorithme d’entrée zéro. Imprimez le code ASCII de chacune des lettres de l’alphabet du système informatique.
Sortie: Un algorithme doit avoir au moins un résultat souhaitable, c’est-à-dire une sortie.
Efficacité : Un algorithme doit être efficace. Efficace signifie que chaque étape doit être considérée comme un principe et doit s’exécuter en temps fini. Exemple de Non efficacité: Trouvez la valeur exacte de e en utilisant la formule suivante:
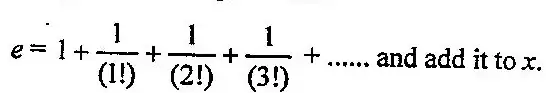
Lire Aussi / Comment Développer Des Compétences Comportementales De Classe Mondiale?
Il n’est pas efficace car il nécessite la sommation de termes infinis. Par conséquent, cela prend un temps infini et n’est donc pas efficace.