Connaissances supposées
Les étudiants auront eu une vaste expérience informelle de la géométrie au cours des années précédentes, ce qui fournira une bonne base intuitive pour l’approche plus systématique de la géométrie appropriée dans les années 7 à 10. Les sujets particuliers des années F−6 pertinents pour ce module sont:
- L’utilisation de compas et de règles et le dessin soigné de figures géométriques.
- Types d’angles, y compris au moins les angles droits, les angles aigus, les angles obtus et les angles réflexes
. - Triangles, y compris une introduction informelle aux triangles isocèles et équilatéraux.
- Quadrilatères, y compris une introduction informelle aux carrés, rectangles, parallélogrammes, trapèzes et losanges.
- Expérience informelle avec translations, réflexions, rotations et agrandissements,
et avec symétrie dans le cadre d’activités telles que le pliage d’un triangle isocèle, d’un rectangle ou d’un losange.
Motivation
 La géométrie est utilisée pour modéliser le monde qui nous entoure. Une vue sur les toits des maisons révèle des triangles, des trapèzes et des rectangles, tandis que les motifs de carrelage des trottoirs et des salles de bains utilisent des hexagones, des pentagones, des triangles et des carrés.
La géométrie est utilisée pour modéliser le monde qui nous entoure. Une vue sur les toits des maisons révèle des triangles, des trapèzes et des rectangles, tandis que les motifs de carrelage des trottoirs et des salles de bains utilisent des hexagones, des pentagones, des triangles et des carrés.
Constructeurs, carreleurs, architectes, graphistes et concepteurs de sites Web utilisent régulièrement des idées géométriques dans leur travail. La classification de tels objets géométriques et l’étude de leurs propriétés sont très importantes. La géométrie a également de nombreuses applications dans l’art.
Tout comme l’arithmétique a des nombres comme objets d’étude de base, les points, les lignes et les cercles sont les éléments de base de la géométrie plane.
En géométrie secondaire, nous commençons par un certain nombre d’idées intuitives (points, lignes et angles) qui ne sont pas du tout faciles à définir avec précision, suivies de quelques définitions (angles opposés verticalement, lignes parallèles, etc.) et nous en déduisons des faits importants, souvent appelés théorèmes. Au secondaire, le niveau de rigueur devrait évoluer lentement d’une année à l’autre, mais à chaque étape, une définition claire est très importante et doit être soulignée.
Ainsi, la géométrie donne l’occasion aux étudiants de développer leur intuition géométrique, qui a des applications dans de nombreux domaines de la vie, et aussi d’apprendre à construire des arguments logiques et à faire des déductions dans un cadre qui est, pour la plupart, indépendant
du nombre.
Contenu
Points et lignes
Les objets les plus simples de la géométrie plane sont les points et les lignes. Parce qu’ils sont si simples, il est difficile d’en donner des définitions précises, alors nous visons plutôt à donner aux étudiants une description approximative de leurs propriétés qui sont conformes à notre intuition. Un point marque une position mais n’a pas de taille. En pratique, lorsque nous dessinons un point, il a clairement une largeur définie, mais il représente un point dans notre imagination. Une ligne n’a pas de largeur et s’étend à l’infini dans les deux sens. Lorsque nous dessinons une ligne, elle a de la largeur et des extrémités, ce n’est donc pas vraiment une ligne, mais représente une ligne dans notre imagination. Étant donné deux points distincts A et B, il y a une (et une seule) ligne qui passe par les deux points. Nous utilisons des lettres majuscules pour désigner des points et des lignes de noms soit en indiquant deux points sur la ligne, soit en utilisant des lettres minuscules telles que  et m. Ainsi, la ligne donnée ci-dessous est appelée ligne AB ou ligne
et m. Ainsi, la ligne donnée ci-dessous est appelée ligne AB ou ligne  .
.

Étant donné deux lignes distinctes, il y a deux possibilités : elles peuvent se rencontrer en un seul point ou elles peuvent ne jamais se rencontrer, quelle que soit la distance à laquelle elles sont étendues (ou produites). Les lignes qui ne se rencontrent jamais sont appelées parallèles. Dans le deuxième diagramme, nous écrivons AB// CD.
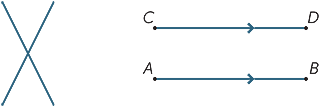
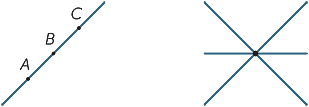
Trois points (ou plus) qui se trouvent sur une ligne droite sont appelés colinéaires.
Trois lignes (ou plus) qui se rencontrent en un seul point sont appelées simultanées.
|
|
|
| Colinéaire |
Concurrent |
Exercice 1
Tracez trois lignes qui ne sont pas simultanées de sorte qu’il n’y en ait pas deux parallèles.
Exercice 2
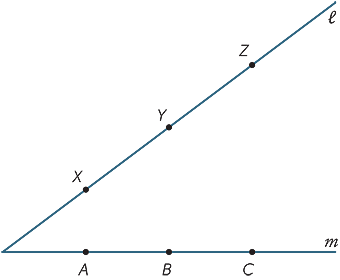
Faites une grande copie du diagramme ci-dessous. Les points X, Y, Z sont tous les points de la ligne  et A, B, C sont tous les points de la ligne m. Join AY et XB appellent leur intersection R. Join BZ et YC et appellent leur intersection P. Join CX et ZA et appellent leur intersection Q. Que remarquez-vous des points P, Q, R? (Ce résultat est appelé théorème de Pappus, vers 340 après JC.)
et A, B, C sont tous les points de la ligne m. Join AY et XB appellent leur intersection R. Join BZ et YC et appellent leur intersection P. Join CX et ZA et appellent leur intersection Q. Que remarquez-vous des points P, Q, R? (Ce résultat est appelé théorème de Pappus, vers 340 après JC.)
Intervalles, Rayons et Angles
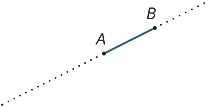 Supposons que A et B soient deux points sur une ligne. L’intervalle
Supposons que A et B soient deux points sur une ligne. L’intervalle
AB est la partie de la ligne entre A et B, y compris les deux extrémités.
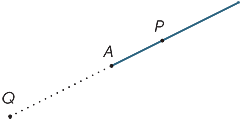 Le point A du diagramme divise la ligne en deux parties appelées rayons. Le rayon AP est le rayon qui contient le point P (et le point A).
Le point A du diagramme divise la ligne en deux parties appelées rayons. Le rayon AP est le rayon qui contient le point P (et le point A).
Angles
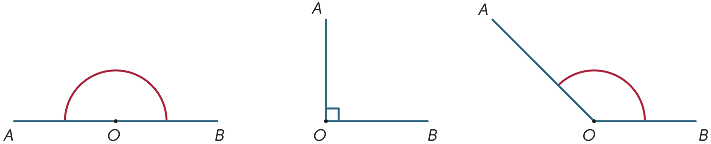
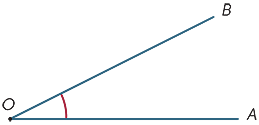
 Dans le diagramme, la région ombrée entre les rayons OA et OB est appelée angle AOB ou angle BOA. Le signe d’angle
Dans le diagramme, la région ombrée entre les rayons OA et OB est appelée angle AOB ou angle BOA. Le signe d’angle ![]() est écrit donc nous écrivons
est écrit donc nous écrivons ![]() AOB.
AOB.
 La région ombrée à l’extérieur s’appelle l’angle réflexe formé par OA et OB. La plupart du temps, à moins de spécifier le mot réflexe, tous nos angles se réfèrent à la zone entre les rayons et non à l’extérieur d’eux.
La région ombrée à l’extérieur s’appelle l’angle réflexe formé par OA et OB. La plupart du temps, à moins de spécifier le mot réflexe, tous nos angles se réfèrent à la zone entre les rayons et non à l’extérieur d’eux.
La Taille d’un angle
 Imaginez que le rayon OB tourne autour du point O jusqu’à ce qu’il se trouve le long de OA. La quantité de rotation est appelée la taille de l’angle AOB. Nous pouvons également définir la taille de l’angle réflexe.
Imaginez que le rayon OB tourne autour du point O jusqu’à ce qu’il se trouve le long de OA. La quantité de rotation est appelée la taille de l’angle AOB. Nous pouvons également définir la taille de l’angle réflexe.
Nous utiliserons souvent de petites lettres grecques, α, β, γ,… pour représenter la taille d’un angle.
La taille de l’angle correspondant à une révolution complète a été divisée (par les Babyloniens) en 360 parties égales, que nous appelons degrés. (Ils ont probablement choisi 360 car c’était proche du nombre de jours dans une année.) Par conséquent, la taille d’un angle droit est de 180 ° et la taille d’un angle droit est de 90 °. D’autres angles peuvent être mesurés (approximativement) à l’aide d’un rapporteur.
|
|
||
| Angle droit | Angle droit |
Angle obtus |
Les angles sont classés en fonction de leur taille. Nous disons qu’un angle de taille α est aigu
(un mot signifiant ‘pointu’) si 0° < α < 90°, α est obtus (un mot signifiant ‘émoussé’) si
90° < α < 180° et α est réflexe si 180° < α < 360°.
Étant donné que le rapporteur a deux échelles, les élèves doivent être prudents lors du dessin et
mesurer les angles. C’est un exercice intéressant d’utiliser un rapporteur pour dessiner des angles tels que 30°, 78°, 130°, 163°.
Exercice 3
 Pliez une feuille de papier A4 correspondant aux coins opposés (en diagonale). Tracez une ligne le long du pli formé et mesurez les angles entre le pli et le côté.
Pliez une feuille de papier A4 correspondant aux coins opposés (en diagonale). Tracez une ligne le long du pli formé et mesurez les angles entre le pli et le côté.
Dans l’exercice ci-dessus, les deux angles forment ensemble une ligne droite et s’ajoutent ainsi à 180°. Deux angles qui s’ajoutent à 180° sont appelés angles supplémentaires; ainsi 45° et 135° sont des angles supplémentaires.
Deux angles qui s’ajoutent à 90° sont dits complémentaires ; ainsi 23° et 67° sont des angles
complémentaires.
Angles en un point
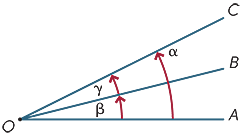 Deux angles en un point sont dits adjacents s’ils partagent un rayon commun. Par conséquent, dans le diagramme,
Deux angles en un point sont dits adjacents s’ils partagent un rayon commun. Par conséquent, dans le diagramme, ![]() AOB et
AOB et ![]() BOC sont adjacents.
BOC sont adjacents.
Des angles adjacents peuvent être ajoutés, donc dans le diagramme
α = β + γ.
Lorsque deux lignes se croisent, quatre angles sont formés au point d’intersection.
Dans le diagramme, les angles marqués ![]() AOX et
AOX et ![]() BOY sont appelés verticalement opposés.
BOY sont appelés verticalement opposés.
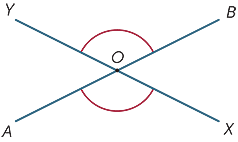 Depuis
Depuis
-
 AOX est le supplément de la BOÎTE
AOX est le supplément de la BOÎTE  (angle droit).
(angle droit). -
 BOY est aussi le complément de la BOÎTE
BOY est aussi le complément de la BOÎTE  (angle droit),
(angle droit),
nous pouvons conclure que ces angles opposés verticalement,
![]() AOX et
AOX et ![]() BOY sont égaux. Nous avons donc notre première
BOY sont égaux. Nous avons donc notre première
déclaration géométrique importante:
Les angles opposés verticalement sont égaux.
Un résultat en géométrie (et en mathématiques en général) est souvent appelé théorème. Un théorème est une déclaration importante qui peut être prouvée par déduction logique. L’argument ci-dessus est une preuve du théorème; parfois, les preuves sont présentées formellement après l’énoncé du théorème.
 Si deux lignes se croisent de sorte que les quatre angles sont perpendiculaires, alors les lignes sont dites perpendiculaires.
Si deux lignes se croisent de sorte que les quatre angles sont perpendiculaires, alors les lignes sont dites perpendiculaires.
Angles en un point – Arguments géométriques
Les raisons suivantes peuvent être utilisées dans les arguments géométriques:
- Les angles adjacents peuvent être ajoutés ou soustraits.
- Les angles en révolution s’ajoutent à 360°.
- Les angles en ligne droite s’ajoutent à 180°.
- Les angles opposés verticalement sont égaux.
Lignes Transversales et Parallèles
 Une transversale est une ligne qui rencontre deux autres lignes.
Une transversale est une ligne qui rencontre deux autres lignes.
Angles correspondants
Différents angles sont formés par la transversale. Dans les diagrammes ci-dessous, les deux angles marqués sont appelés angles correspondants.
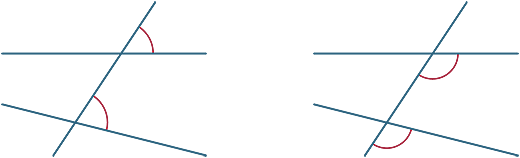
 Nous regardons maintenant ce qui se passe lorsque les deux lignes coupées par la transversale sont parallèles.
Nous regardons maintenant ce qui se passe lorsque les deux lignes coupées par la transversale sont parallèles.
Inituitivement, si l’angle α était supérieur à β alors CD croiserait AB à gauche de F et s’il était inférieur à β, il se croiserait à droite de F. Ainsi, puisque les lignes ne se croisent pas du tout, α ne peut être ni inférieur ni supérieur à β et donc égal à β.
Alternativement, imaginez traduire l’angle QGD le long de GF jusqu’à ce que G coïncide avec F. Puisque les lignes sont parallèles, nous nous attendrions à ce que l’angle α coïncide avec l’angle β. Cette observation nous amène à conjecturer que:
Les angles correspondants formés de lignes parallèles sont égaux.
Nous ne pouvons pas prouver ce résultat, bien que nous ayons montré qu’il est géométriquement plausible. Nous l’accepterons comme un axiome de la géométrie. Un axiome est une affirmation que nous ne pouvons pas prouver, mais qui est intuitivement raisonnable. Notez que de nombreux faits que nous avons déjà énoncés, tels que: des angles adjacents peuvent être ajoutés, et deux points déterminent une ligne, etc., sont également des axiomes, bien que nous ne les ayons pas explicitement énoncés de cette manière.
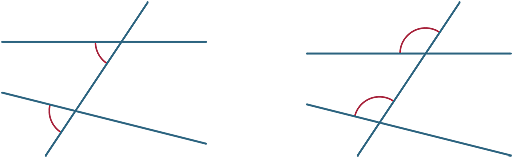
Angles alternatifs
Dans chaque diagramme, les deux angles marqués sont appelés angles alternatifs (car ils se trouvent sur des côtés alternatifs de la transversale).

 Si les lignes AB et CD sont parallèles, les angles alternatifs sont égaux. Ce résultat peut maintenant être prouvé.
Si les lignes AB et CD sont parallèles, les angles alternatifs sont égaux. Ce résultat peut maintenant être prouvé.
![]() DGQ = α (angles correspondants, AB//CD)
DGQ = α (angles correspondants, AB//CD)
![]() DGQ = β (angles opposés verticalement à G)
DGQ = β (angles opposés verticalement à G)
Donc α = β.
Pour résumer:
Les angles alternés formés de lignes parallèles sont égaux.
Angles co-intérieurs
Enfin, dans chaque diagramme ci-dessous, les deux angles marqués sont appelés angles co-intérieurs et se trouvent du même côté de la transversale.

Si les droites AB et CD sont parallèles, il est évident que les angles co-intérieurs ne sont pas égaux mais il s’avère qu’ils sont supplémentaires, c’est-à-dire que leur somme est de 180°.
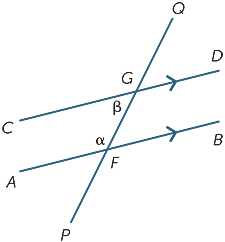 C’est un résultat qui est également facile à prouver:
C’est un résultat qui est également facile à prouver:
![]() BFG = β (angles alternatifs, AB||CD)
BFG = β (angles alternatifs, AB||CD)
α + β = 180° (angle droit à F)
Pour résumer:
Les angles Co-intérieurs formés à partir de lignes parallèles sont supplémentaires.
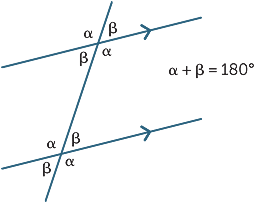 Les trois résultats peuvent être résumés
Les trois résultats peuvent être résumés
par le diagramme suivant:
Exemples numériques
Compte tenu des informations sur les angles d’un diagramme, nous pouvons utiliser les résultats ci-dessus pour trouver la taille des autres angles du diagramme. C’est une compétence simple mais très importante, souvent appelée de manière informelle chasse d’angle. Dans la résolution de problèmes, la séquence d’étapes n’est pas toujours unique. Il peut y avoir plusieurs approches différentes, mais tout aussi valables.
Par exemple, dans le diagramme suivant, nous cherchons la taille de l’angle BAC.

![]() DCA = 102° (angles alternés, AC/BD)
DCA = 102° (angles alternés, AC/BD)
![]() BAC = 78° (angles co-intérieurs, AB//CD)
BAC = 78° (angles co-intérieurs, AB//CD)
Exercice 4
Utilisez une séquence alternatie d’étapes pour trouver ![]() BAC.
BAC.
Exercice 5
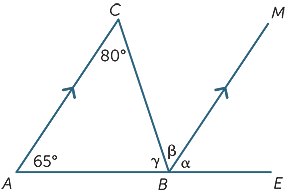 En utilisant uniquement les propriétés des lignes parallèles, trouvez (avec les raisons) les angles manquants dans le diagramme suivant.
En utilisant uniquement les propriétés des lignes parallèles, trouvez (avec les raisons) les angles manquants dans le diagramme suivant.
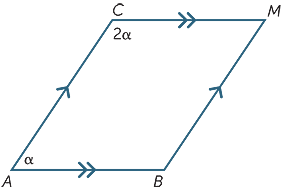
Exercice 6
Trouvez la valeur de α dans le diagramme suivant.
Instructions inverses
De nombreuses instructions en mathématiques ont une inverse, dans laquelle l’implication va dans la direction opposée. Par exemple, l’instruction
‘ Chaque nombre pair se termine par 0, 2, 4, 6 ou 8.’
a converse
‘ Chaque nombre qui se termine par 0, 2, 4, 6 ou 8 est pair.’
Cette déclaration particulière et son inverse sont tous deux vrais, mais ce n’est en aucun cas toujours le cas
.
Par exemple, les deux instructions suivantes sont des inverses l’une de l’autre :
‘Chaque multiple de 4 est un nombre pair.’
‘ Chaque nombre pair est un multiple de 4.’
et ici, la première déclaration est vraie, mais la seconde est fausse.
Exercice 7
Notez:
a ![]() un vrai énoncé géométrique dont l’inverse est également vrai,
un vrai énoncé géométrique dont l’inverse est également vrai,
b ![]() un faux énoncé géométrique dont l’inverse est vrai,
un faux énoncé géométrique dont l’inverse est vrai,
c ![]() un faux énoncé géométrique dont l’inverse est également faux.
un faux énoncé géométrique dont l’inverse est également faux.
Les Théorèmes Inverses pour les Lignes parallèles
Nous avons vu que les angles correspondants formés à partir de lignes parallèles sont égaux. Nous pouvons écrire l’énoncé inverse comme suit. Instruction
: Si les lignes sont parallèles, les angles correspondants sont égaux.
Converse: Si les angles correspondants sont égaux, les lignes sont parallèles.
L’instruction inverse est également vraie et est souvent utilisée pour prouver que deux lignes sont parallèles. Il en va de même pour les angles alternés et co-intérieurs. Instruction
: Si les lignes sont parallèles, les angles alternatifs sont égaux.
Converse : Si les angles alternatifs sont égaux, les lignes sont parallèles.
Déclaration: Si les lignes sont parallèles, les angles co-intérieurs sont supplémentaires.
Converse: Si les angles co-intérieurs sont supplémentaires, alors les lignes sont parallèles.
Ainsi, dans chaque diagramme, les lignes AB et CD sont parallèles.

Exercice 8
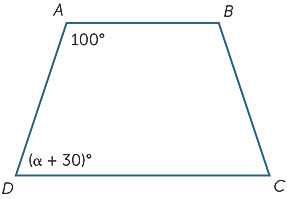 Quelle valeur de α rendra AB parallèle à CD ?
Quelle valeur de α rendra AB parallèle à CD ?
Preuves des Trois Inverses
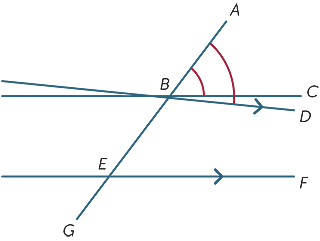 Nous supposons que les angles correspondants formés par la transversale sont égaux et nous montrons que les lignes sont parallèles.
Nous supposons que les angles correspondants formés par la transversale sont égaux et nous montrons que les lignes sont parallèles.
Dans le diagramme, nous supposons que
![]() ABC =
ABC = ![]() BEF.
BEF.
Si BC et EF ne sont pas parallèles, dessinez
BD parallèlement à EF.
Maintenant puisque BD et EF sont parallèles ![]() ABD =
ABD = ![]() BEF et donc
BEF et donc ![]() ABC =
ABC = ![]() ABD ce qui est clairement impossible à moins que les lignes BC et BD ne soient identiques. Les droites BC et EF sont donc parallèles.
ABD ce qui est clairement impossible à moins que les lignes BC et BD ne soient identiques. Les droites BC et EF sont donc parallèles.
Les autres épreuves suivent de la même manière.
L’exercice 9
Donne une preuve du second théorème inverse (angles alternatifs).
Somme d’angle d’un triangle
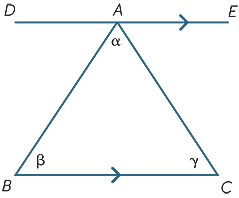 Les résultats de la section précédente peuvent être utilisés pour déduire l’un des faits les plus importants en géométrie − la somme des angles d’un triangle est de 180°.
Les résultats de la section précédente peuvent être utilisés pour déduire l’un des faits les plus importants en géométrie − la somme des angles d’un triangle est de 180°.
Nous commençons par le triangle ABC avec les angles α, β, γ comme indiqué. Tracez la ligne DAE parallèle à BC. Puis,
![]() DAB = β (angles alternés, BC|/DE)
DAB = β (angles alternés, BC|/DE)
![]() EAC = γ (angles alternatifs, BC||DE)
EAC = γ (angles alternatifs, BC||DE)
α + β + γ = 180° (angle droit).
Ainsi, nous avons prouvé le théorème
La somme des angles dans un triangle est de 180°.
Un quadrilatère est une figure plane délimitée par quatre côtés.
Exercice 10
En divisant le quadrilatère ABCD en deux triangles, trouvez la somme des angles.
Liens vers l’avant
Le matériau de ce module a commencé à placer la géométrie sur une base raisonnablement systématique d’objets soigneusement définis, d’axiomes à supposer et de théorèmes que nous avons prouvés. Sur cette base, nous pouvons développer un compte rendu systématique de la géométrie plane impliquant:
- Théorème de Pythagore
- congruence et triangles congruents
- similitude et triangles similaires
- triangles isocèles et équilatéraux
- quadrilatères spéciaux, y compris les carrés, les rectangles, les parallélogrammes, les losanges et les trapèzes
- la géométrie des cercles.
La géométrie plane sera également fondamentale dans de nombreux autres domaines des mathématiques des années 7 à 10:
- transformations
- géométrie tridimensionnelle
- aires et volumes
- trigonométrie
- géométrie des coordonnées
- les graphes des cercles et des paraboles.
Les idées de tangentes et d’aires conduisent à leur tour au calcul dans les années 11-12.
Histoire et application
Histoire
Les constructions incroyables des pyramides et des immenses temples d’Égypte révèlent que les Égyptiens devaient avoir une très bonne connaissance pratique et compréhension de la géométrie de base, au moins au niveau pratique. D’autre part, rien ne prouve qu’ils aient systématisé cette connaissance de quelque manière formelle que ce soit. Cela a été laissé aux anciens Grecs. Nous n’avons pas de connaissance détaillée de cette systématisation, à l’exception de l’affirmation selon laquelle Thales (ca. 624 av.J.-C. 546 av. J.-C.) a donné les premières « preuves » de faits géométriques qui ont marqué les débuts de la géométrie déductive. L’École Pythagoricienne a poursuivi ce travail et Platon (428 av.J.-C. -348 av. J.-C.) s’inspire clairement du travail des mathématiciens antérieurs lorsqu’il mentionne des faits géométriques dans ses écrits. Le dialogue géométrique de son œuvre le Ménon, dans lequel Socrate fait parvenir à un esclave un théorème géométrique par une série de déductions logiques, vaut la peine d’être lu. Si les origines de la géométrie ne sont pas claires, le « produit final » ne l’est pas. Euclide (323-283 avant JC), écrivant à Alexandrie, a produit un travail remarquable, appelé les Éléments, qui est resté le manuel standard en géométrie pendant plus de 2000 ans. Dans ce travail, Euclide expose un certain nombre de définitions (comme pour les points et les lignes), de postulats et de notions communes. (De nos jours, nous les appelons axiomes.) À partir de ceux-ci, il développa logiquement, dans un ordre très soigneusement choisi, un grand nombre de théorèmes que nous appelons généralement Géométrie euclidienne. Il y a un certain nombre d’autres résultats géométriques, tels que le théorème de Pappus, qui ont été découverts après Euclide, mais ceux-ci ne sont généralement pas couverts à l’école secondaire.
L’un des cinq postulats d’Euclide n’était pas aussi évident que les autres semblaient l’être. Une version de celui-ci, connue sous le nom d’axiome de Playfair, stipule que: Étant donné une ligne  et un point P, pas sur
et un point P, pas sur  , il y a une et une seule ligne parallèle à
, il y a une et une seule ligne parallèle à  passant par P. Au 19ème siècle, un certain nombre de mathématiciens ont posé la question « Que se passe-t-il si nous refusons ce postulat? »Cela se fait en supposant qu’il n’y a pas de telle ligne parallèle, ou en disant qu’il y a plus d’une telle ligne. Cela a conduit au développement de géométries non euclidiennes, dont l’une s’est avérée fournir l’un des bons modèles pour l’univers.
passant par P. Au 19ème siècle, un certain nombre de mathématiciens ont posé la question « Que se passe-t-il si nous refusons ce postulat? »Cela se fait en supposant qu’il n’y a pas de telle ligne parallèle, ou en disant qu’il y a plus d’une telle ligne. Cela a conduit au développement de géométries non euclidiennes, dont l’une s’est avérée fournir l’un des bons modèles pour l’univers.
Applications
Dans un sens très réel, la géométrie et l’intuition géométrique constituent les fondements de toutes les mathématiques
− la géométrie conduit à la géométrie des coordonnées qui conduit au calcul et à
toutes ses nombreuses applications – et est donc cruciale dans le programme.
Sur un plan plus pratique, les constructeurs, les géomètres, les ingénieurs et les architectes ont été de grands utilisateurs de la géométrie et des idées géométriques pendant des siècles. Plus récemment, avec le développement des ordinateurs, des graphistes et des concepteurs de sites Web ont rejoint ce groupe de personnes qui ont besoin et utilisent la géométrie dans leur travail. Lorsqu’on lui a récemment demandé à quel point la géométrie est utile, Jim Kelly, un scientifique appliqué a déclaré:… la géométrie est une partie importante de la conception, du dessin et de la modélisation informatique. Il est également utilisé fréquemment dans… cours de physique et d’autres sciences physiques dans le cadre de la compréhension des effets des charges sur les structures et les points d’équilibrage (centres de gravité) pour les solides composites. En chimie, comprendre la géométrie d’une molécule est lié à la compréhension des propriétés des substances. De nombreux autres exemples existent. (sur le site de Ask a Scientist.)
Une histoire des mathématiques: Une introduction, 3e Édition, Victor J. Katz, Addison-Wesley, (2008)
Histoire des mathématiques, D. E. Smith, Dover publications New York, (1958)
RÉPONSES AUX EXERCICES
EXERCICE 1
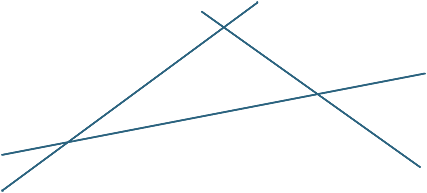
EXERCICE 2
Les points sont colinéaires
EXERCICE 3
60°
EXERCICE 4
![]() DBA = 102° (angles correspondants, AB//CD)
DBA = 102° (angles correspondants, AB//CD)
![]() BAC = 78° (angles co-intérieurs, AC|| BD)
BAC = 78° (angles co-intérieurs, AC|| BD)
EXERCICE 5
α = 65° ![]() (angles correspondants, AC|| BM)
(angles correspondants, AC|| BM)
β = 80° ![]() (angles alternatifs, AC|| BM)
(angles alternatifs, AC|| BM)
γ +β = 115° ![]() (angles co-intérieurs, AC|| BM angles, AC//BM)
(angles co-intérieurs, AC|| BM angles, AC//BM)
Par conséquent, γ = 35°
( C’est la structure pour une preuve du résultat que la somme des angles d’un triangle est de 180°)
EXERCICE 6
α = 60°
EXERCICE 7
a ![]() Un quadrilatère avec chacun de ses angles intérieurs un angle droit est un rectangle.
Un quadrilatère avec chacun de ses angles intérieurs un angle droit est un rectangle.
Converse: Chaque angle intérieur d’un rectangle est un angle droit.
b ![]() Un rectangle est un carré
Un rectangle est un carré
Converse: Un carré est un rectangle
c ![]() La somme des angles intérieurs d’un triangle est de 200°
La somme des angles intérieurs d’un triangle est de 200°
Converse: Un polygone pour lequel la somme de l’angle intérieur est de 200° est un triangle.
EXERCICE 8
α= 50°
EXERCICE 9
Nous nous référons au même diagramme.
Placez un point H sur la ligne EF à gauche de E.
![]() CBE =
CBE = ![]() BEH
BEH
Si BC et EF ne sont pas parallèles, dessinez BD parallèlement à EF.
Puisque BD et EF sont parallèles, ![]() EBD =
EBD = ![]() BEH, ce qui est clairement impossible à moins que les lignes BC et BD ne soient identiques.
BEH, ce qui est clairement impossible à moins que les lignes BC et BD ne soient identiques.
Les lignes BC et EF sont donc parallèles.
EXERCICE 10
360°
Le projet Improving Mathematics Education in Schools (TIMES) 2009-2011 a été financé par le Ministère australien de l’Éducation, de l’Emploi et des Relations sur le lieu de Travail.
Les points de vue exprimés ici sont ceux de l’auteur et ne représentent pas nécessairement les points de vue du Ministère australien de l’Éducation, de l’Emploi et des Relations sur le lieu de travail.
© L’Université de Melbourne au nom du Centre International d’Excellence pour l’Éducation en Mathématiques (ICE-EM), division de l’éducation de l’Australian Mathematical Sciences Institute (AMSI), 2010 (sauf indication contraire). Ce travail est sous licence Creative Commons Attribution- NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()