Ce sera aujourd’hui une brève introduction aux statistiques circulaires (parfois appelées statistiques directionnelles). La statistique circulaire est une subdivision intéressante des statistiques impliquant des observations prises comme vecteurs autour d’un cercle unitaire. À titre d’exemple, imaginez la mesure des heures de naissance dans un hôpital sur un cycle de 24 heures, ou la dispersion directionnelle d’un groupe d’animaux migrateurs. Ce type de données est impliqué dans divers domaines, tels que l’écologie, la climatologie et la biochimie. La nature de la mesure des observations autour d’un cercle unitaire nécessite une approche différente des tests d’hypothèses. Les distributions doivent être « enroulées » autour du cercle pour être utiles, et les estimateurs conventionnels tels que la moyenne de l’échantillon ou la variance de l’échantillon ne contiennent pas d’eau.
Dans cet article, nous effectuerons le test d’espacement de Rao pour évaluer l’uniformité d’un ensemble de données circulaire. Il s’agit d’une procédure de base et doit être considérée comme une introduction au traitement des données circulaires.
Mise en route
Nous allons effectuer un test d’hypothèse sur les tortues, un petit ensemble de données composé des angles d’arrivée de 10 tortues vertes sur leur île de nidification. Notre objectif est de déterminer où les angles d’arrivée montrent des signes de directionnalité ou sont plus indicatifs d’une dispersion aléatoire.
Tout d’abord, installez le package circular et attachez le jeu de données turtles.
install.packages("circular")require(circular)attach(turtles)
Traçage des données
Le paquet circular contient sa propre fonction de traçage, plot.circular. Observons les angles d’arrivée des tortues.
plot.circular(arrival)
Voici l’intrigue: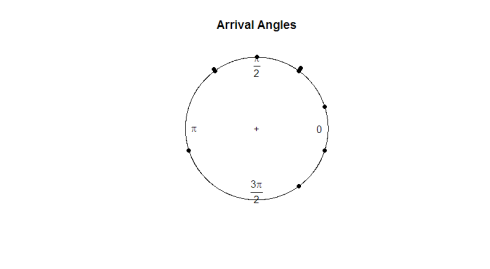
Compte tenu du test oculaire, les observations semblent être uniformes autour du cercle. Si nous voulons exécuter un test d’hypothèse pour déterminer si les données sont vraiment uniformes, nous devrons développer une statistique de test qui fonctionne avec des données angulaires.
Quel est un bon paramètre à utiliser pour nous? Prendre la moyenne de l’échantillon ne nous dit pas grand-chose sur la direction des données (180 degrés n’est pas une moyenne utile de 2 degrés et 358 degrés). Dans le graphique suivant, observez en quoi la moyenne de l’échantillon ne sert à rien pour représenter la forme ou la propagation de nos données.
mean(arrival)plot.circular(mean(arrival)) 0.9120794
Voici l’intrigue: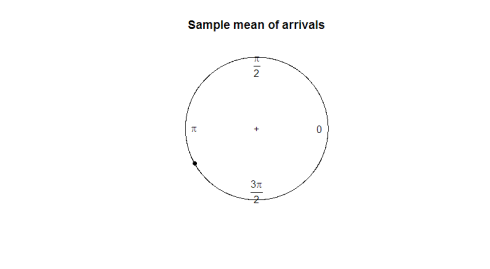
Au lieu de cela, nous utiliserons une méthode qui détermine la directionnalité en mesurant l’espace moyen entre les observations. Ce test est appelé Test d’espacement de Rao.
Essai d’espacement de Rao
Le test d’espacement de Rao a été développé pour évaluer l’uniformité des données circulaires. Il utilise l’espace entre les observations pour déterminer si les données montrent une directionnalité significative. Si les données sont uniformes, les observations devraient avoir tendance à être espacées uniformément.
Voici la statistique de test \(U\) pour le test d’espacement de Rao: $$U = 1/2\somme\limites_ {i = 1}^n|T_{i}–λ| λ où \(λ= 360/n, T_{i} = f_{i+1}-f_{i}\) et \(T_{n} =(360-f_{n}) +f_{1}\)
Fondamentalement, la statistique de test agrège les écarts entre les points consécutifs, chacun pondéré par le nombre total d’observations dans l’ensemble de données.
Nous utiliserons la fonction rao.spacing.test() pour exécuter ce test d’hypothèses. Notre hypothèse nulle dit que les données sont d’une distribution uniforme, tandis que l’autre indique que les données montrent des signes de directionnalité. Faisons le test.
rao.spacing.test(arrival,alpha=.10) Rao's Spacing Test of Uniformity Test Statistic = 127.2689 Level 0.1 critical value = 161.23 Do not reject null hypothesis of uniformity
Avec une statistique de test de 127 tombant en dessous de la valeur critique de 161, les données ne penchent pas de manière significative dans aucune direction. Nous ne pouvons pas rejeter l’hypothèse selon laquelle les arrivées de tortues sont d’une distribution uniforme.
Conclusion
Le test d’espacement de Rao a déterminé que les données ne montraient aucun signe de tendance directionnelle. Nous ne pouvons pas rejeter l’hypothèse nulle de l’uniformité et assumerons l’uniformité en ce qui concerne le sens d’arrivée. Bien que cet article soit un tutoriel relativement basique, de nombreuses personnes de la communauté de la science des données n’ont jamais travaillé avec des données circulaires auparavant. C’est un sous-thème intéressant à explorer ainsi qu’un jeune domaine de la statistique qui évolue encore.
Remarques finales
J’aimerais remercier S. Rao Jammalamadaka PhD, de l’Université de Californie à Santa Barbara, et son manuel « Topics in Circular Statistics » pour avoir suscité mon intérêt dans le domaine des statistiques circulaires.