4.2 Estimation des Coefficients du Modèle de Régression Linéaire

En pratique, l’ordonnée à l’origine $\beta_0$ et la pente $\beta_1$ de la droite de régression de population sont inconnues. Par conséquent, nous devons utiliser des données pour estimer les deux paramètres inconnus. Dans ce qui suit, un exemple du monde réel sera utilisé pour démontrer comment cela est réalisé. Nous voulons relier les résultats des tests aux ratios élèves-enseignants mesurés dans les écoles californiennes. Le score du test est la moyenne à l’échelle du district des scores en lecture et en mathématiques pour les élèves de cinquième année. Encore une fois, la taille de la classe est mesurée comme le nombre d’élèves divisé par le nombre d’enseignants (le ratio élèves-enseignants). En ce qui concerne les données, l’ensemble de données des écoles de Californie (CASchools) est livré avec un package R appelé AER, un acronyme pour Économétrie appliquée avec R (Kleiber et Zeileis 2020). Après avoir installé le package avec install.paquets (« AER ») et l’attacher à la bibliothèque (AER) l’ensemble de données peut être chargé à l’aide de la fonction data().

## # install the AER package (once)## install.packages("AER")## ## # load the AER packagelibrary(AER)# load the the data set in the workspacedata(CASchools)

Une fois qu’un paquet a été installé, il est disponible pour être utilisé à d’autres occasions lorsqu’il est appelé avec library() — il n’est pas nécessaire d’exécuter install.packages() encore une fois!

Il est intéressant de savoir à quel type d’objet nous avons affaire.class() renvoie la classe d’un objet. Selon la classe d’un objet, certaines fonctions (par exemple plot() et summary()) se comportent différemment.

Vérifions la classe de l’objet CASchools.

class(CASchools)#> "data.frame"

Il s’avère que CASchools est de données de classe.cadre qui est un format pratique avec lequel travailler, en particulier pour effectuer une analyse de régression.

Avec l’aide de head(), nous obtenons un premier aperçu de nos données. Cette fonction affiche uniquement les 6 premières lignes de l’ensemble de données, ce qui empêche une sortie de console surpeuplée.

Appuyez sur ctrl+L pour effacer la console. Cette commande supprime tout code tapé et exécuté par vous ou imprimé sur la console par R functions. La bonne nouvelle est que tout le reste est laissé intact. Vous ne perdez ni les variables définies, etc. ni l’historique du code. Il est toujours possible de rappeler les commandes R précédemment exécutées à l’aide des touches haut et bas. Si vous travaillez dans RStudio, appuyez sur ctrl + Haut sur votre clavier (CMD + Haut sur un Mac) pour consulter une liste de commandes saisies précédemment.

head(CASchools)#> district school county grades students teachers#> 1 75119 Sunol Glen Unified Alameda KK-08 195 10.90#> 2 61499 Manzanita Elementary Butte KK-08 240 11.15#> 3 61549 Thermalito Union Elementary Butte KK-08 1550 82.90#> 4 61457 Golden Feather Union Elementary Butte KK-08 243 14.00#> 5 61523 Palermo Union Elementary Butte KK-08 1335 71.50#> 6 62042 Burrel Union Elementary Fresno KK-08 137 6.40#> calworks lunch computer expenditure income english read math#> 1 0.5102 2.0408 67 6384.911 22.690001 0.000000 691.6 690.0#> 2 15.4167 47.9167 101 5099.381 9.824000 4.583333 660.5 661.9#> 3 55.0323 76.3226 169 5501.955 8.978000 30.000002 636.3 650.9#> 4 36.4754 77.0492 85 7101.831 8.978000 0.000000 651.9 643.5#> 5 33.1086 78.4270 171 5235.988 9.080333 13.857677 641.8 639.9#> 6 12.3188 86.9565 25 5580.147 10.415000 12.408759 605.7 605.4

Nous constatons que l’ensemble de données est composé de nombreuses variables et que la plupart d’entre elles sont numériques.

Au fait: une alternative à class() et head() est str() qui est déduite de ‘structure’ et donne un aperçu complet de l’objet. Essaie!

Pour en revenir aux CASchools, les deux variables qui nous intéressent (i.e., le score moyen au test et le ratio élèves-enseignants) ne sont pas inclus. Cependant, il est possible de calculer les deux à partir des données fournies. Pour obtenir les ratios élèves-enseignants, il suffit de diviser le nombre d’élèves par le nombre d’enseignants. Le score moyen du test est la moyenne arithmétique du score du test pour la lecture et du score du test de mathématiques. Le bloc de code suivant montre comment les deux variables peuvent être construites en tant que vecteurs et comment elles sont ajoutées à CASchools.

# compute STR and append it to CASchoolsCASchools$STR <- CASchools$students/CASchools$teachers # compute TestScore and append it to CASchoolsCASchools$score <- (CASchools$read + CASchools$math)/2

Si nous exécutions à nouveau head (CASchools), nous trouverions les deux variables d’intérêt sous forme de colonnes supplémentaires nommées STR et score (vérifiez ceci!).

Le tableau 4.1 du manuel résume la distribution des résultats aux tests et des ratios élèves-enseignants. Plusieurs fonctions peuvent être utilisées pour produire des résultats similaires, par ex.,

mean() (calcule la moyenne arithmétique des nombres fournis),
sd() (calcule l’écart type de l’échantillon),
quantile() (renvoie un vecteur des quantiles d’échantillon spécifiés pour les données).

Le morceau de code suivant montre comment y parvenir. Tout d’abord, nous calculons des statistiques sommaires sur les colonnes STR et score des CASchools. Afin d’obtenir une sortie agréable, nous rassemblons les mesures dans une donnée.cadre nommé DistributionSummary.

# compute sample averages of STR and scoreavg_STR <- mean(CASchools$STR) avg_score <- mean(CASchools$score)# compute sample standard deviations of STR and scoresd_STR <- sd(CASchools$STR) sd_score <- sd(CASchools$score)# set up a vector of percentiles and compute the quantiles quantiles <- c(0.10, 0.25, 0.4, 0.5, 0.6, 0.75, 0.9)quant_STR <- quantile(CASchools$STR, quantiles)quant_score <- quantile(CASchools$score, quantiles)# gather everything in a data.frame DistributionSummary <- data.frame(Average = c(avg_STR, avg_score), StandardDeviation = c(sd_STR, sd_score), quantile = rbind(quant_STR, quant_score))# print the summary to the consoleDistributionSummary#> Average StandardDeviation quantile.10. quantile.25. quantile.40.#> quant_STR 19.64043 1.891812 17.3486 18.58236 19.26618#> quant_score 654.15655 19.053347 630.3950 640.05000 649.06999#> quantile.50. quantile.60. quantile.75. quantile.90.#> quant_STR 19.72321 20.0783 20.87181 21.86741#> quant_score 654.45000 659.4000 666.66249 678.85999

En ce qui concerne les exemples de données, nous utilisons plot(). Cela nous permet de détecter des caractéristiques de nos données, telles que des valeurs aberrantes qui sont plus difficiles à découvrir en regardant de simples nombres. Cette fois, nous ajoutons des arguments supplémentaires à l’appel de plot().

Le premier argument de notre appel à plot(), score ~STR, est à nouveau une formule qui énonce des variables sur l’axe y et l’axe x. Cependant, cette fois, les deux variables ne sont pas enregistrées dans des vecteurs séparés mais sont des colonnes de CASchools. Par conséquent, R ne les trouverait pas sans que les données d’argument soient correctement spécifiées. les données doivent être conformes au nom des données.trame à laquelle appartiennent les variables, dans ce cas CASchools. D’autres arguments sont utilisés pour modifier l’apparence du tracé : tandis que main ajoute un titre, xlab et ylab ajoutent des étiquettes personnalisées aux deux axes.

plot(score ~ STR, data = CASchools, main = "Scatterplot of TestScore and STR", xlab = "STR (X)", ylab = "Test Score (Y)")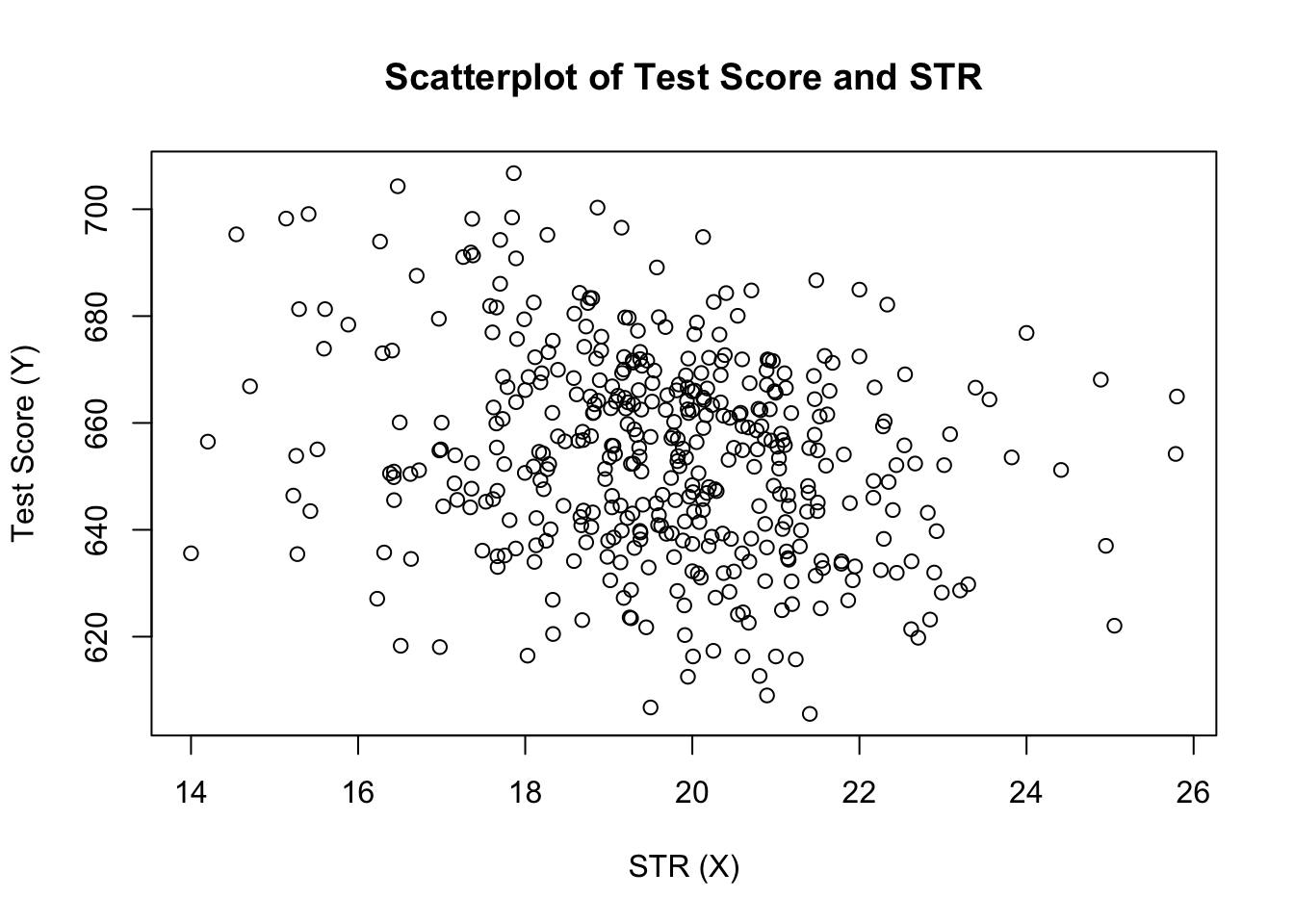

Le graphique (Figure 4.2 dans le livre) montre le nuage de points de toutes les observations sur le ratio élèves-enseignants et le score au test. Nous voyons que les points sont fortement dispersés et que les variables sont corrélées négativement. Autrement dit, nous nous attendons à observer des scores de test plus bas dans les classes plus grandes.

La fonction cor() (voir ?cor pour plus d’informations) peut être utilisé pour calculer la corrélation entre deux vecteurs numériques.

cor(CASchools$STR, CASchools$score)#> -0.2263627

Comme le suggère déjà le nuage de points, la corrélation est négative mais plutôt faible.

La tâche à laquelle nous sommes maintenant confrontés est de trouver une ligne qui correspond le mieux aux données. Bien sûr, nous pourrions simplement nous en tenir à l’inspection graphique et à l’analyse de corrélation, puis sélectionner la meilleure ligne d’ajustement en regardant. Cependant, ce serait plutôt subjectif: différents observateurs dessineraient des lignes de régression différentes. Sur ce compte, nous nous intéressons à des techniques moins arbitraires. Une telle technique est donnée par l’estimation des moindres carrés ordinaires (OLS).

L’Estimateur des Moindres Carrés ordinaires

L’estimateur OLS choisit les coefficients de régression de telle sorte que la droite de régression estimée soit aussi » proche » que possible des points de données observés. Ici, la proximité est mesurée par la somme des erreurs au carré commises dans la prédiction $Y$ donnée $X$. Soit $b_0$ et $b_1$ quelques estimateurs de $\beta_0$ et $\beta_1$. Ensuite, la somme des erreurs d’estimation au carré peut être exprimée comme suit

L’estimateur OLS dans le modèle de régression simple est la paire d’estimateurs pour l’interception et la pente qui minimise l’expression ci-dessus. La dérivation des estimateurs OLS pour les deux paramètres est présentée à l’annexe 4.1 du livre. Les résultats sont résumés dans le Concept clé 4.2.

L’estimateur OLS, les Valeurs prédites et les Résidus

Les estimateurs OLS de la pente $\beta_1$ et de l’ordonnée à l’origine $\beta_0$ dans le modèle de régression linéaire simple sont \Les valeurs prédites OLS $\widehat{Y}_i$ et les résidus $\hat{u}_i$ sont \

L’ordonnée à l’origine estimée $\hat{\ beta}_0$, le paramètre de pente $\hat{\beta}_1$ et les résidus $\left(\hat{u}_i\right)$ sont calculés à partir d’un échantillon d’observations $n$ de $X_i$ et $Y_i$, $i$, $…$, $et$. Ce sont des estimations de l’interception inconnue de la population $\left(\beta_0\right)$, de la pente $\left(\beta_1\right)$ et du terme d’erreur $(u_i)$.

Les formules présentées ci-dessus peuvent ne pas être très intuitives à première vue. L’application interactive suivante vise à vous aider à comprendre les mécanismes de l’OLS. Vous pouvez ajouter des observations en cliquant sur le système de coordonnées où les données sont représentées par des points. Une fois que deux observations ou plus sont disponibles, l’application calcule une ligne de régression en utilisant OLS et certaines statistiques qui sont affichées dans le panneau de droite. Les résultats sont mis à jour lorsque vous ajoutez d’autres observations dans le panneau de gauche. Un double-clic réinitialise l’application, c’est-à-dire que toutes les données sont supprimées.

Il existe de nombreuses façons de calculer $\hat{\beta}_0$ et $\hat{\beta}_1$ dans R. Par exemple, nous pourrions implémenter les formules présentées dans Key Concept 4.2 avec deux des fonctions les plus élémentaires de R: mean() et sum(). Avant de le faire, nous attachons le jeu de données CASchools.

attach(CASchools) # allows to use the variables contained in CASchools directly# compute beta_1_hatbeta_1 <- sum((STR - mean(STR)) * (score - mean(score))) / sum((STR - mean(STR))^2)# compute beta_0_hatbeta_0 <- mean(score) - beta_1 * mean(STR)# print the results to the consolebeta_1#> -2.279808beta_0#> 698.9329

Appeler attach (CASchools) nous permet d’adresser une variable contenue dans CASchools par son nom: il n’est plus nécessaire d’utiliser l’opérateur $ en conjonction avec l’ensemble de données : R peut évaluer directement le nom de la variable.

R utilise l’objet dans l’environnement utilisateur si cet objet partage le nom de la variable contenue dans une base de données jointe. Cependant, il est préférable de toujours utiliser des noms distinctifs afin d’éviter de telles ambivalences (apparemment)!

Notez que nous adressons directement les variables contenues dans le jeu de données ci-joint CASchools pour le reste de ce chapitre !

Bien sûr, il existe encore plus de moyens manuels pour effectuer ces tâches. L’OLS étant l’une des techniques d’estimation les plus utilisées, R contient bien sûr déjà une fonction intégrée nommée lm() (modèle linéaire) qui peut être utilisée pour effectuer une analyse de régression.

Le premier argument de la fonction à spécifier est, similaire à plot(), la formule de régression avec la syntaxe de base y ~x où y est la variable dépendante et x la variable explicative. Les données d’argument déterminent l’ensemble de données à utiliser dans la régression. Nous revenons maintenant sur l’exemple du livre où la relation entre les résultats des tests et la taille des classes est analysée. Le code suivant utilise lm() pour reproduire les résultats présentés dans la figure 4.3 du livre.

# estimate the model and assign the result to linear_modellinear_model <- lm(score ~ STR, data = CASchools)# print the standard output of the estimated lm object to the console linear_model#> #> Call:#> lm(formula = score ~ STR, data = CASchools)#> #> Coefficients:#> (Intercept) STR #> 698.93 -2.28

Ajoutons la ligne de régression estimée au graphique. Cette fois, nous élargissons également les plages des deux axes en définissant les arguments xlim et ylim.

# plot the dataplot(score ~ STR, data = CASchools, main = "Scatterplot of TestScore and STR", xlab = "STR (X)", ylab = "Test Score (Y)", xlim = c(10, 30), ylim = c(600, 720))# add the regression lineabline(linear_model)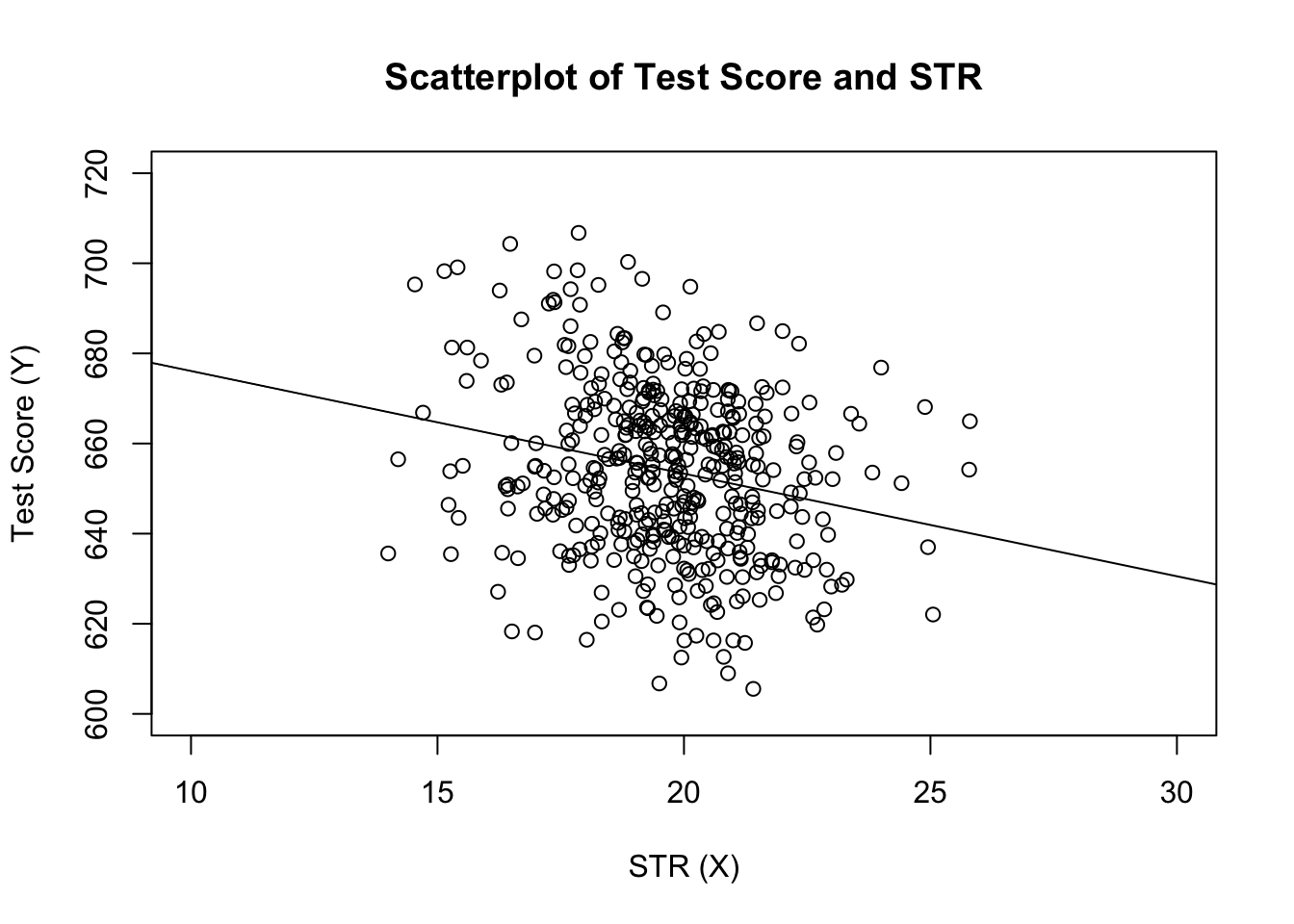

Avez-vous remarqué que cette fois, nous n’avons pas transmis les paramètres d’interception et de pente à abline? Si vous appelez abline() sur un objet de classe lm qui ne contient qu’un seul régresseur, R dessine automatiquement la ligne de régression !

Introduction à l’Économétrie avec R