Ceci est un guide étape par étape sur la façon d’exécuter une analyse de cluster k-means sur une feuille de calcul Excel du début à la fin. Veuillez noter qu’un modèle Excel qui exécute automatiquement l’analyse de cluster est disponible en téléchargement gratuit sur ce site Web. Mais si vous voulez savoir comment exécuter vous-même un clustering k-means sur Excel, cet article est pour vous.
En plus de cet article, j’ai également une présentation vidéo de la façon d’exécuter une analyse de cluster dans Excel.
- Première étape – Commencez avec votre ensemble de données
- Deuxième étape – Si seulement deux variables, utilisez un graphique de dispersion sur Excel
- Troisième étape – Calculez la distance entre chaque point de données et le centre d’un cluster
- Comment fonctionne le calcul?
- Quatrième étape – Calculer la moyenne (moyenne) de chaque ensemble de grappes
- Cinquième étape – Répétez l’étape 3 – la distance par rapport à la moyenne révisée
- Étape finale – Graphez et résumez les clusters
Première étape – Commencez avec votre ensemble de données
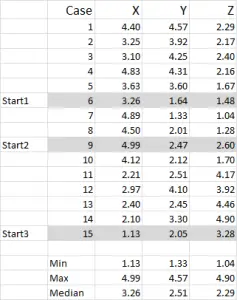
Figure 1
Pour cet exemple, j’utilise 15 cas (ou répondants), où nous avons les données pour trois variables – étiquetées de manière générique X, Y et Z.
Vous devriez remarquer que les données sont mises à l’échelle 1-5 dans cet exemple. Vos données peuvent être sous n’importe quelle forme, à l’exception d’une échelle de données nominale (voir l’article sur les données à utiliser).
REMARQUE: Je préfère utiliser des données mises à l’échelle – mais ce n’est pas obligatoire. La raison en est de « contenir » les valeurs aberrantes. Disons, par exemple, que j’utilise des données sur le revenu (une mesure démographique) – la plupart des données peuvent se situer entre 40 000 $ et 100 000 $, mais j’ai une personne avec un revenu de 5 millions de dollars. Il est tout simplement plus facile pour moi de classer cette personne dans la tranche de revenu « supérieure à 250 000 $ » et d’échelonner le revenu de 1 à 9 – mais cela dépend de vous selon les données avec lesquelles vous travaillez.
Vous pouvez voir dans cet exemple que trois positions de départ ont été mises en évidence – nous en discuterons à la troisième étape ci-dessous.
Deuxième étape – Si seulement deux variables, utilisez un graphique de dispersion sur Excel
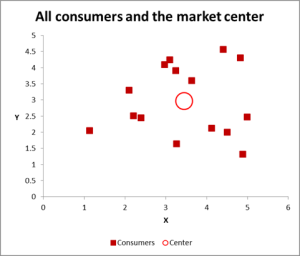
Figure 2
Dans cet exemple d’analyse de cluster, nous utilisons trois variables – mais si vous n’avez que deux variables à regrouper, un graphique en nuage de points est un excellent moyen de commencer. Et, parfois, vous pouvez regrouper les données via des moyens visuels.
Comme vous pouvez le voir dans ce graphique à dispersion, chaque cas individuel (ce que j’appelle un consommateur pour cet exemple) a été mappé, ainsi que la moyenne (moyenne) pour tous les cas (le cercle rouge).
Selon la façon dont vous affichez les données / le graphique, il semble y avoir un certain nombre de clusters. Dans ce cas, vous pouvez identifier trois ou quatre clusters relativement distincts, comme le montre le graphique suivant.
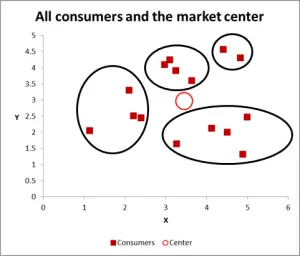
Figure 3
Avec ce graphique suivant, j’ai visiblement identifié le cluster probable et les ai encerclés. Comme je l’ai suggéré, une bonne approche lorsqu’il n’y a que deux variables à considérer – mais est–ce le cas, nous avons trois variables (et vous pourriez en avoir plus), donc cette approche visuelle ne fonctionnera que pour les ensembles de données de base – alors voyons maintenant comment faire le calcul Excel pour le clustering k-means.
Troisième étape – Calculez la distance entre chaque point de données et le centre d’un cluster
Pour cet exemple, supposons que nous voulons identifier trois segments / clusters uniquement. Oui, il y a quatre clusters évidents dans le diagramme ci-dessus, mais cela ne regarde que deux des variables. Veuillez noter que vous pouvez utiliser cette approche Excel pour identifier autant de clusters que vous le souhaitez – suivez simplement le même concept que celui expliqué ci-dessous.
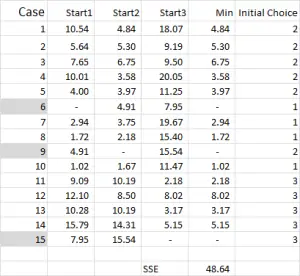
Figure 4
Pour le clustering k-means, vous choisissez généralement des cas aléatoires (points de départ ou graines) pour démarrer l’analyse.
Dans cet exemple – comme je veux créer trois clusters, j’aurai besoin de trois points de départ. Pour ces points de départ, j’ai sélectionné les cas 6, 9 et 15 – mais tous les points aléatoires pourraient également convenir.
La raison pour laquelle j’ai sélectionné ces cas est que – en regardant uniquement la variable X – le cas 6 était la médiane, le cas 9 était le maximum et le cas 15 était le minimum. Cela suggère que ces trois cas sont quelque peu différents les uns des autres, si bons points de départ car ils sont étalés.
Veuillez vous référer à l’article expliquant pourquoi l’analyse de cluster génère parfois des résultats différents.
Se référant à la sortie de la table – c’est notre premier calcul dans Excel et cela génère notre « choix initial » de clusters. Le début 1 est les données pour le cas 6, le début 2 est le cas 9 et le début 3 est le cas 15. Vous devez noter que l’intersection de chacun d’entre eux donne un 0 (-) dans le tableau.
Comment fonctionne le calcul?
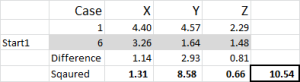
Figure 5
Regardons le premier nombre du tableau – cas 1, commencez 1 = 10,54.
Rappelez-vous que nous avons arbitrairement désigné le cas 6 comme notre point de départ aléatoire pour le cluster 1. Nous voulons calculer la distance et nous utilisons la méthode de la somme des carrés – comme indiqué ici. Nous calculons la différence entre chacun des trois points de données de l’ensemble, puis plaçons les différences au carré, puis les additionnons.
Nous pouvons le faire « mécaniquement » comme indiqué ici – mais Excel a une formule intégrée à utiliser: SUMXMY2 – c’est beaucoup plus efficace à utiliser.
En revenant à la figure 4, nous trouvons ensuite la distance minimale pour chaque cas à partir de chacun des trois points de départ – cela nous indique le groupe (1, 2 ou 3) dont le cas est le plus proche – qui est indiqué dans la colonne ‘choix initial’.
Quatrième étape – Calculer la moyenne (moyenne) de chaque ensemble de grappes
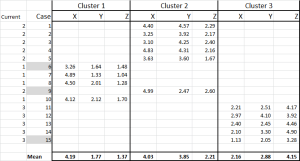
Figure 6
Nous avons maintenant alloué chaque cas à son cluster initial – et nous pouvons le définir à l’aide d’une instruction IF dans un tableau (comme le montre la figure 6).
En bas du tableau, nous avons la moyenne (moyenne) de chacun de ces cas. N0w – au lieu de compter sur un seul point de données « représentatif » – nous avons un ensemble de cas représentant chacun.
Cinquième étape – Répétez l’étape 3 – la distance par rapport à la moyenne révisée
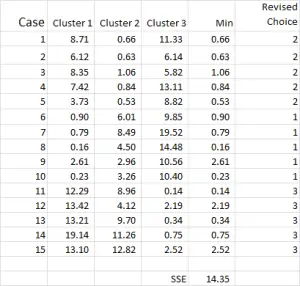
Figure 7
Le processus d’analyse des clusters consiste maintenant à répéter les étapes 4 et 5 (itérations) jusqu’à ce que les clusters se stabilisent.
Chaque fois que nous utilisons la moyenne révisée pour chaque cluster. Par conséquent, la figure 7 montre notre deuxième itération – mais cette fois, nous utilisons les moyens générés au bas de la figure 6 (au lieu des points de départ de la figure 1).
Vous pouvez maintenant voir qu’il y a eu un léger changement dans l’application du cluster, le cas 9 – l’un de nos points de départ – étant réaffecté.
Vous pouvez également voir la somme de l’erreur au carré (SSE) calculée en bas – qui est la somme de chacune des distances minimales. Notre objectif est maintenant de répéter les étapes 4 et 5 jusqu’à ce que l’ESS ne montre qu’une amélioration minimale et / ou que les modifications d’allocation de cluster soient mineures à chaque itération.
Étape finale – Graphez et résumez les clusters
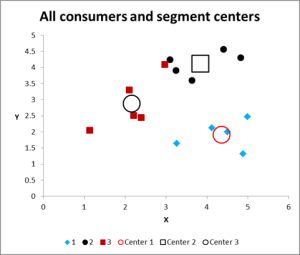
Figure 8
Après avoir exécuté plusieurs itérations, nous avons maintenant la sortie pour représenter graphiquement et résumer les données.
Voici le graphique de sortie pour cet exemple Excel d’analyse de cluster.
Comme vous pouvez le voir, il y a trois clusters distincts montrés, ainsi que les centroïdes (moyenne) de chaque cluster – les symboles les plus grands.
Nous pouvons également présenter ces données sous forme de tableau si nécessaire, comme nous l’avons élaboré dans Excel.
Jetez un coup d’œil au cas du cluster 3 – le petit carré rouge juste à côté du point noir en haut au milieu du graphique. Ce cas se trouve là en raison de l’influence de la troisième variable, qui n’est pas montrée sur ce graphique à deux variables.