Selon Noam Chomosky, il existe quatre types de grammaires − Type 0, Type 1, Type 2 et Type 3. Le tableau suivant montre en quoi ils diffèrent les uns des autres −
| Type de grammaire | Grammaire acceptée | Langue acceptée | Automate |
|---|---|---|---|
| Type 0 | Grammaire illimitée | Langage récursivement énumérable | Machine de Turing |
| Type 1 | Grammaire contextuelle | Langage contextuel | Automate borné linéaire |
| Type 2 | Grammaire sans contexte | Langage sans contexte | Automate de poussée |
| Type 3 | Grammaire régulière | Langage régulier | Automate à états finis |
Jetez un coup d’œil à l’illustration suivante. Il montre la portée de chaque type de grammaire −
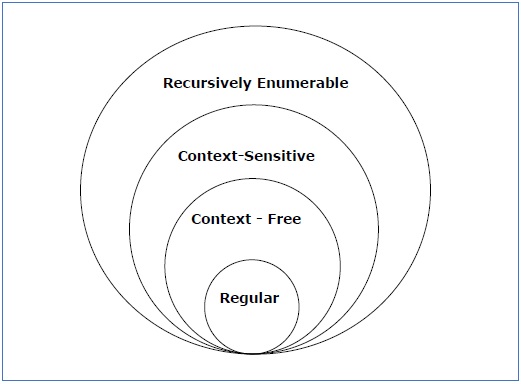
Grammaire de type 3
Les grammaires de type 3 génèrent des langages réguliers. Les grammaires de type 3 doivent avoir un seul non-terminal sur le côté gauche et un côté droit composé d’un seul terminal ou d’un seul terminal suivi d’un seul non-terminal.
Les productions doivent être sous la forme X → a ou X → aY
où X, Y ∈ N (Non terminal)
et a ∈ T (Terminal)
La règle S → ε est autorisée si S n’apparaît pas à droite d’une règle.
Exemple
X → ε X → a | aYY → b
Grammaire de type 2
Les grammaires de type 2 génèrent des langages sans contexte.
Les productions doivent être sous la forme A → γ
où A ∈ N (Non terminal)
et γ ∈ (T ∪ N)* (Chaîne de terminaux et de non-terminaux).
Ces langages générés par ces grammaires sont reconnus par un automate pushdown non déterministe.
Exemple
S → X a X → a X → aX X → abc X → ε
Grammaire de type 1
Les grammaires de type 1 génèrent des langages sensibles au contexte. Les productions doivent se présenter sous la forme
α A β → α γ β
où A ∈ N (Non terminal)
et α, β, γ ∈ (T ∪ N) * (Chaînes de terminaux et non-terminaux)
Les chaînes α et β peuvent être vides, mais γ doit être non vide.
La règle S → ε est autorisée si S n’apparaît pas sur le côté droit d’une règle. Les langages générés par ces grammaires sont reconnus par un automate borné linéaire.
Exemple
AB → AbBc A → bcA B → b
Grammaire de type 0
Les grammaires de type 0 génèrent des langages énumérables récursivement. Les productions n’ont aucune restriction. Ce sont n’importe quelle grammaire de structure de phase, y compris toutes les grammaires formelles.
Ils génèrent les langages reconnus par une machine de Turing.
Les productions peuvent être sous la forme de α → β où α est une chaîne de terminaux et de non terminaux avec au moins un non terminal et α ne peut pas être nul. β est une chaîne de terminaux et de non-terminaux.
Exemple
S → ACaB Bc → acB CB → DB aD → Db