Évaluation | Biopsychologie | Comparative | Cognitive | Développementale | Langage | Différences individuelles | Personnalité | Philosophie | Social |
Méthodes | Statistiques | Articles cliniques | Éducatifs | Industriels | Professionnels | Psychologie du monde |
Statistiques: Méthode scientifique · Méthodes de recherche · Conception expérimentale · Cours de statistiques de premier cycle · Tests statistiques · Théorie des jeux · Théorie de la décision
Veuillez aider à améliorer cette page vous-même si vous le pouvez..
L’analyse de grappes ou clustering est une technique courante d’analyse de données statistiques, utilisée dans de nombreux domaines, notamment l’apprentissage automatique, l’exploration de données, la reconnaissance de formes, l’analyse d’images et la bioinformatique. Le clustering est la classification d’objets similaires en différents groupes, ou plus précisément, le partitionnement d’un ensemble de données en sous-ensembles (clusters), de sorte que les données de chaque sous-ensemble partagent (idéalement) un trait commun – souvent la proximité selon une mesure de distance définie.
Outre le terme de regroupement de données (ou simplement de regroupement), il existe un certain nombre de termes ayant des significations similaires, notamment l’analyse de cluster, la classification automatique, la taxonomie numérique, la botryologie et l’analyse typologique.
- Types de clustering
- Regroupement hiérarchique
- Mesure de distance
- Création de clusters
- Clustering hiérarchique agglomératif
- Clustering partitionnel
- k-moyennes et dérivées
- K-moyennes clustering
- Algorithme QT Clust
- C flou – signifie clustering
- Critère du coude
- Clustering spectral
- Applications
- Biologie
- Recherche marketing
- Autres applications
- Comparaisons entre les regroupements de données
- Voir aussi
- Bibliographie
- Implémentations logicielles
- Gratuites
Types de clustering
Les algorithmes de clustering de données peuvent être hiérarchiques ou partitionnels. Les algorithmes hiérarchiques trouvent des clusters successifs à l’aide de clusters précédemment établis, tandis que les algorithmes partitionnels déterminent tous les clusters à la fois. Les algorithmes hiérarchiques peuvent être agglomératifs (de bas en haut) ou divisifs (de haut en bas). Les algorithmes d’agglomération commencent par chaque élément en tant que cluster séparé et les fusionnent en clusters successivement plus grands. Les algorithmes de division commencent par l’ensemble et le divisent en clusters successivement plus petits.
Regroupement hiérarchique
Mesure de distance
Une étape clé dans un regroupement hiérarchique consiste à sélectionner une mesure de distance. Une mesure simple est la distance de Manhattan, égale à la somme des distances absolues pour chaque variable. Le nom vient du fait que dans un cas à deux variables, les variables peuvent être tracées sur une grille qui peut être comparée aux rues de la ville, et la distance entre deux points est le nombre de blocs qu’une personne marcherait.
Une mesure plus courante est la distance euclidienne, calculée en trouvant le carré de la distance entre chaque variable, en additionnant les carrés et en trouvant la racine carrée de cette somme. Dans le cas à deux variables, la distance est analogue à la recherche de la longueur de l’hypoténuse dans un triangle; c’est-à-dire que c’est la distance « à vol d’oiseau. »Une revue de l’analyse en grappes dans la recherche en psychologie de la santé a révélé que la mesure de distance la plus courante dans les études publiées dans ce domaine de recherche est la distance euclidienne ou la distance euclidienne au carré.
Création de clusters
Étant donné une mesure de distance, les éléments peuvent être combinés. Le clustering hiérarchique construit (agglomératif), ou se décompose (divisif), une hiérarchie de clusters. La représentation traditionnelle de cette hiérarchie est une structure de données arborescente (appelée dendrogramme), avec des éléments individuels à une extrémité et un seul cluster avec chaque élément à l’autre. Les algorithmes d’agglomération commencent en haut de l’arbre, tandis que les algorithmes de division commencent en bas. (Sur la figure, les flèches indiquent un regroupement agglomératif.)
Couper l’arbre à une hauteur donnée donnera un clustering à une précision sélectionnée. Dans l’exemple suivant, la coupe après la deuxième ligne donnera des grappes {a}{b c}{d e}{f}. La coupe après la troisième ligne donnera des clusters {a} {b c} {d e f}, qui sont des clusters plus grossiers, avec moins de clusters plus gros.
Clustering hiérarchique agglomératif
Par exemple, supposons que ces données doivent être regroupées. Où la distance euclidienne est la métrique de distance.
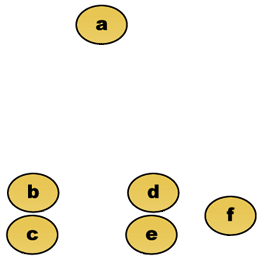
Données brutes
Le dendrogramme de clustering hiérarchique serait en tant que tel:
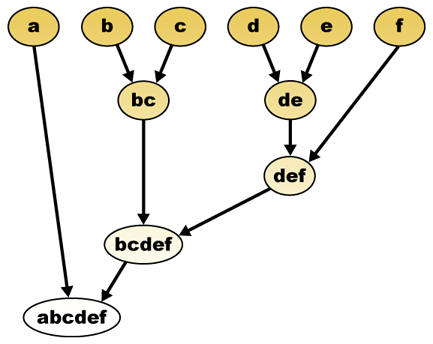
Représentation traditionnelle
Cette méthode construit la hiérarchie à partir des éléments individuels en fusionnant progressivement les clusters. Encore une fois, nous avons six éléments {a} {b} {c} {d} {e} et {f}. La première étape consiste à déterminer les éléments à fusionner dans un cluster. Habituellement, nous voulons prendre les deux éléments les plus proches, nous devons donc définir une distance 
Supposons que nous ayons fusionné les deux éléments les plus proches b et c, nous avons maintenant les clusters suivants {a}, {b, c}, {d}, {e} et {f}, et nous voulons les fusionner davantage. Mais pour ce faire, nous devons prendre la distance entre {a} et {b c}, et donc définir la distance entre deux clusters. Habituellement, la distance entre deux grappes 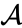
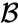
- La distance maximale entre les éléments de chaque cluster (également appelée clustering de liaison complet):
- La distance minimale entre les éléments de chaque cluster (également appelée cluster à liaison unique):
- La distance moyenne entre les éléments de chaque grappe (également appelée grappe de liaison moyenne):
- La somme de toute la variance intra-cluster
- L’augmentation de la variance pour le cluster fusionné (critère de Ward)
- La probabilité que les clusters candidats apparaissent à partir de la même fonction de distribution (liaison en V)
Chaque agglomération se produit à une plus grande distance entre les clusters que l’agglomération précédente, et on peut décider d’arrêter le clustering soit lorsque les clusters sont trop éloignés pour être fusionnés (critère de distance) ou lorsqu’il y a un nombre suffisamment faible de grappes (critère de nombre).
Clustering partitionnel
k-moyennes et dérivées
K-moyennes clustering
L’algorithme K-moyennes attribue chaque point au cluster dont le centre (également appelé centroïde) est le plus proche. Le centre est la moyenne de tous les points du cluster — c’est-à-dire que ses coordonnées sont la moyenne arithmétique pour chaque dimension séparément sur tous les points du cluster.
Exemple: L’ensemble de données a trois dimensions et le cluster a deux points : X =(x1, x2, x3) et Y = (y1, y2, y3). Alors le centroïde Z devient Z =(z1, z2, z3), où z1 = (x1 + y1)/2 et z2 =(x2 + y2)/2 et z3 = (x3 + y3)/2.
L’algorithme est approximativement (J. MacQueen, 1967):
- Générez aléatoirement k grappes et déterminez les centres de grappes, ou générez directement k points de départ en tant que centres de grappes.
- Attribuez chaque point au centre de cluster le plus proche.
- Recalculez les nouveaux centres de cluster.
- Répétez jusqu’à ce qu’un critère de convergence soit satisfait (généralement que l’affectation n’a pas changé).
Les principaux avantages de cet algorithme sont sa simplicité et sa rapidité qui lui permettent de s’exécuter sur de grands ensembles de données. Son inconvénient est qu’il ne donne pas le même résultat à chaque exécution, car les clusters résultants dépendent des affectations aléatoires initiales. Il maximise la variance inter-cluster (ou minimise la variance intra-cluster), mais ne garantit pas que le résultat a un minimum global de variance.
Algorithme QT Clust
Le clustering QT (Seuil de qualité) (Heyer et al, 1999) est une méthode alternative de partitionnement des données, inventée pour le clustering de gènes. Il nécessite plus de puissance de calcul que k-means, mais ne nécessite pas de spécifier a priori le nombre de clusters, et renvoie toujours le même résultat lorsqu’il est exécuté plusieurs fois.
L’algorithme est:
- L’utilisateur choisit un diamètre maximum pour les clusters.
- Construisez un cluster candidat pour chaque point en incluant le point le plus proche, le plus proche, etc., jusqu’à ce que le diamètre du cluster dépasse le seuil.
- Enregistrez le cluster candidat avec le plus de points en tant que premier vrai cluster et supprimez tous les points du cluster de toute considération ultérieure.
- Récursionner avec l’ensemble réduit de points.
La distance entre un point et un groupe de points est calculée en utilisant une liaison complète, c’est-à-dire comme la distance maximale entre le point et n’importe quel membre du groupe (voir la section « Clustering hiérarchique agglomératif » sur la distance entre les clusters).
C flou – signifie clustering
Dans le clustering flou, chaque point a un degré d’appartenance à des clusters, comme dans la logique floue, plutôt que d’appartenir complètement à un seul cluster. Ainsi, les points sur le bord d’un cluster peuvent être dans le cluster à un degré moindre que les points au centre du cluster. Pour chaque point x, nous avons un coefficient donnant le degré d’être dans le kème cluster 

Avec des moyennes en c floues, le centroïde d’un cluster est la moyenne de tous les points, pondérée par leur degré d’appartenance au cluster :
Le degré d’appartenance est lié à l’inverse de la distance au cluster
ensuite, les coefficients sont normalisés et flous avec un paramètre réel 
Pour m égal à 2, cela équivaut à normaliser le coefficient linéairement pour faire leur somme 1. Lorsque m est proche de 1, le centre du cluster le plus proche du point reçoit beaucoup plus de poids que les autres, et l’algorithme est similaire aux k-moyennes.
L’algorithme flou des moyennes en c est très similaire à l’algorithme des moyennes en k:
- Choisissez un certain nombre de clusters.
- Attribuez aléatoirement à chaque point des coefficients pour être dans les clusters.
- Répétez jusqu’à ce que l’algorithme ait convergé (c’est-à-dire que la variation des coefficients entre deux itérations ne dépasse pas
, le seuil de sensibilité donné) :
- Calculez le centroïde pour chaque cluster, en utilisant la formule ci-dessus.
- Pour chaque point, calculez ses coefficients d’être dans les clusters, en utilisant la formule ci-dessus.
L’algorithme minimise également la variance intra-cluster, mais présente les mêmes problèmes que les k-moyennes, le minimum est un minimum local et les résultats dépendent du choix initial des poids.
Critère du coude
Le critère du coude est une règle empirique courante pour déterminer le nombre de grappes à choisir, par exemple pour les moyennes-k et le clustering hiérarchique agglomératif.
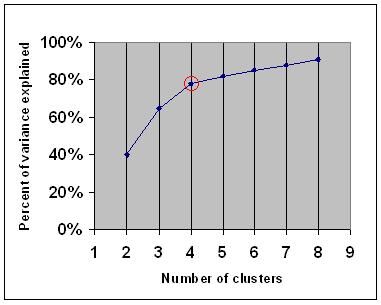
Le critère du coude indique que vous devez choisir un certain nombre de clusters afin que l’ajout d’un autre cluster n’ajoute pas suffisamment d’informations. Plus précisément, si vous représentez graphiquement le pourcentage de variance expliqué par les clusters par rapport au nombre de clusters, les premiers clusters ajouteront beaucoup d’informations (expliquent beaucoup de variance), mais à un moment donné, le gain marginal diminuera, donnant un angle dans le graphique (le coude).
Sur le graphique suivant, le coude est indiqué par le cercle rouge. Le nombre de grappes choisies devrait donc être de 4.
Clustering spectral
Étant donné un ensemble de points de données, la matrice de similarité peut être définie comme une matrice 


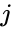
L’une de ces techniques est l’algorithme de Shi-Malik, couramment utilisé pour la segmentation d’images. Il divise les points en deux ensembles 

de 
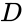
Ce partitionnement peut être effectué de différentes manières, par exemple en prenant la médiane 



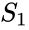
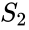
Un algorithme connexe est l’algorithme de Meila-Shi, qui prend les vecteurs propres correspondant aux k valeurs propres les plus grandes de la matrice 
Applications
Biologie
En biologie, le clustering a de nombreuses applications dans les domaines de la biologie computationnelle et de la bioinformatique, dont deux sont:
- En transcriptomique, le regroupement est utilisé pour construire des groupes de gènes avec des modèles d’expression connexes. Souvent, ces groupes contiennent des protéines fonctionnellement liées, telles que des enzymes pour une voie spécifique, ou des gènes co-régulés. Les expériences à haut débit utilisant des étiquettes de séquence exprimées (EST) ou des puces à ADN peuvent être un outil puissant pour l’annotation du génome, un aspect général de la génomique.
- Dans l’analyse de séquences, le regroupement est utilisé pour regrouper des séquences homologues en familles de gènes. C’est un concept très important en bioinformatique et en biologie évolutive en général. Voir évolution par duplication de gènes.
Recherche marketing
L’analyse en grappes est largement utilisée dans les études de marché lorsqu’on travaille avec des données multivariées provenant d’enquêtes et de panels de test. Les chercheurs de marché utilisent l’analyse par grappes pour diviser la population générale de consommateurs en segments de marché et pour mieux comprendre les relations entre différents groupes de consommateurs / clients potentiels.
- Segmenter le marché et déterminer les marchés cibles
- Positionnement du produit
- Développement de nouveaux produits
- Sélection des marchés tests (voir : techniques expérimentales)
Autres applications
Analyse des réseaux sociaux: Dans l’étude des réseaux sociaux, le regroupement peut être utilisé pour reconnaître les communautés au sein de grands groupes de personnes.
Segmentation d’image : Le clustering peut être utilisé pour diviser une image numérique en régions distinctes pour la détection de frontières ou la reconnaissance d’objets.
Exploration de données : De nombreuses applications d’exploration de données impliquent le partitionnement d’éléments de données en sous-ensembles connexes; les applications de marketing discutées ci-dessus en représentent quelques exemples. Une autre application courante est la division des documents, tels que les pages World Wide Web, en genres.
Comparaisons entre les regroupements de données
Plusieurs suggestions ont été faites pour mesurer la similitude entre deux regroupements. Une telle mesure peut être utilisée pour comparer les performances de différents algorithmes de clustering de données sur un ensemble de données. Beaucoup de ces mesures sont dérivées de la matrice d’appariement (ou matrice de confusion), par exemple, la mesure de Rand et les mesures de Fowlkes-Mallows Bk.
- Jain, Murty et Flynn: Regroupement de données: Une revue, Comp. ACM. Surv., 1999. Disponible ici.
- pour une autre présentation des moyennes hiérarchiques, des moyennes k et des moyennes c floues, voir cette introduction au clustering. A également une explication sur le mélange de Gaussiens.
- David Dowe, Page de modélisation des mélanges – autres liens de modèle de clustering et de mélange.
- un tutoriel sur le clustering
- Le manuel en ligne: Théorie de l’information, Inférence et Algorithmes d’apprentissage, de David J.C. MacKay comprend des chapitres sur le clustering des moyennes k, le clustering des moyennes k douces et les dérivations, y compris l’algorithme E-M et la vue variationnelle de l’algorithme E-M.
Voir aussi
- k- signifie
- Réseau de neurones artificiels (ANN)
- Carte auto-organisée
- Maximisation des attentes (EM)
Bibliographie
- Clatworthy, J., Buick, D., Hankins, M., Weinman, J., & Horne, R. (2005). The use and reporting of cluster analysis in health psychology: A review. Journal britannique de psychologie de la santé 10:329-358.
- Romesburg, H. Clarles, Analyse des clusters pour les chercheurs, 2004, 340 p. ISBN 1411606175 ou éditeur, réimpression de l’édition de 1990 publiée par Krieger Pub. Co… Une traduction en japonais est disponible auprès de Uchida Rokakuho Publishing Co., Ltd., Tokyo, Japon.
- Heyer, L.J., Kruglyak, S. et Yooseph, S., Explorer les données d’expression: Identification et Analyse des gènes coexprimés, Genome Research 9:1106-1115.
- Le manuel en ligne: Théorie de l’information, Inférence et Algorithmes d’apprentissage, de David J.C. MacKay comprend des chapitres sur le clustering des moyennes k, le clustering des moyennes k douces et les dérivations, y compris l’algorithme E-M et la vue variationnelle de l’algorithme E-M.
Pour le clustering spectral :
- Jianbo Shi et Jitendra Malik, « Normalized Cuts and Image Segmentation », IEEE Transactions on Pattern Analysis and Machine Intelligence, 22 (8), 888-905, août 2000. Disponible sur la page d’accueil de Jitendra Malik
- Marina Meila et Jianbo Shi, « Learning Segmentation with Random Walk », Neural Information Processing Systems, NIPS, 2001. Disponible sur la page d’accueil de Jianbo Shi
Pour estimer le nombre de grappes:
- Can, F., Ozkarahan, E. A. (1990) « Concepts and effectiveness of the cover coefficient-based clustering methodology for text databases. »Transactions ACM sur les systèmes de base de données. 15 (4) 483-517.
Implémentations logicielles
Gratuites
- le package flexclust pour R
- YALE (Encore un autre environnement d’apprentissage): logiciel open-source gratuit pour la découverte de connaissances et l’exploration de données comprenant également un plugin pour le clustering
- quelques fichiers sources Matlab pour le clustering ici
- COMPACT – Package comparatif pour l’Évaluation du Clustering (également dans Matlab)
- mixmod : Analyse De Cluster Et Discriminante Basée Sur Des Modèles. Code en C++, interface avec Matlab et Scilab
- Tutoriel de clustering LingPipe Tutoriel pour effectuer un clustering complet et à liaison unique à l’aide de LingPipe, un package d’exploration de données de texte Java distribué avec source.
- Weka : Weka contient des outils pour le prétraitement des données, la classification, la régression, le clustering, les règles d’association et la visualisation. Il est également bien adapté au développement de nouveaux schémas d’apprentissage automatique.








