vurdering | Biopsykologi | komparativ | kognitiv |udviklingsmæssig | sprog | individuelle forskelle | personlighed |filosofi | Social |
metoder |statistik | klinisk |uddannelsesmæssig | industriel | professionel items |verdenspsykologi |
statistik:videnskabelig metode · forskningsmetoder · eksperimentelt design · Undergraduate statistik kurser · statistiske tests · spilteori · beslutningsteori
vær venlig at hjælpe med at forbedre denne side selv, hvis du kan..
klyngeanalyse eller klyngedannelse er en almindelig teknik til statistisk dataanalyse, som bruges på mange områder, herunder maskinindlæring, data mining, mønstergenkendelse, billedanalyse og bioinformatik. Klyngedannelse er klassificeringen af lignende objekter i forskellige grupper eller mere præcist opdelingen af et datasæt i undergrupper (klynger), så dataene i hver delmængde (ideelt set) deler noget fælles træk – ofte nærhed i henhold til et defineret afstandsmål.
udover udtrykket data clustering (eller bare clustering) er der en række udtryk med lignende betydninger, herunder klyngeanalyse, automatisk klassificering, numerisk taksonomi, botryologi og typologisk analyse.
- typer af klyngedannelse
- hierarkisk klyngedannelse
- afstandsmåling
- oprettelse af klynger
- Agglomerativ hierarkisk klyngedannelse
- Partitional clustering
- k-midler og derivater
- K-betyder clustering
- CLUSTING algoritme
- uklar c-betyder klyngedannelse
- Albuekriterium
- spektral klyngedannelse
- applikationer
- Biologi
- Marketing research
- andre applikationer
- sammenligninger mellem dataklynger
- Se også
- bibliografi
- programmel implementeringer
- gratis
typer af klyngedannelse
dataklyngealgoritmer kan være hierarkiske eller partitionelle. Hierarkiske algoritmer finder successive klynger ved hjælp af tidligere etablerede klynger, mens partitionsalgoritmer bestemmer alle klynger på en gang. Hierarkiske algoritmer kan være agglomerative (bottom-up) eller splittende (ovenfra og ned). Agglomerative algoritmer begynder med hvert element som en separat klynge og fusionerer dem i successivt større klynger. Splittende algoritmer begynder med hele sættet og fortsætter med at opdele det i successivt mindre klynger.
hierarkisk klyngedannelse
afstandsmåling
et nøgletrin i en hierarkisk klyngedannelse er at vælge en afstandsmåling. En simpel foranstaltning er manhattan afstand, svarende til summen af absolutte afstande for hver variabel. Navnet kommer fra det faktum, at variablerne i en To-variabel sag kan afbildes på et gitter, der kan sammenlignes med byens gader, og afstanden mellem to punkter er antallet af blokke, en person vil gå.
et mere almindeligt mål er euklidisk afstand, beregnet ved at finde kvadratet af afstanden mellem hver variabel, summere firkanterne og finde kvadratroden af denne sum. I det to-variable tilfælde er afstanden analog med at finde længden af hypotenusen i en trekant; det vil sige, det er afstanden “som kragen flyver.”En gennemgang af klyngeanalyse i sundhedspsykologiforskning viste, at den mest almindelige afstandsmåling i offentliggjorte undersøgelser inden for dette forskningsområde er den euklidiske afstand eller den kvadratiske euklidiske afstand.
oprettelse af klynger
givet en afstandsmåling kan elementer kombineres. Hierarkisk klyngedannelse bygger (agglomerativ) eller bryder op (splittende), et hierarki af klynger. Den traditionelle repræsentation af dette hierarki er en trædatastruktur (kaldet et dendrogram) med individuelle elementer i den ene ende og en enkelt klynge med hvert element i den anden. Agglomerative algoritmer begynder øverst på træet, mens splittende algoritmer begynder i bunden. (I figuren angiver pilene en agglomerativ klyngedannelse.)
at skære træet i en given højde giver en klyngedannelse med en valgt præcision. I det følgende eksempel vil skæring efter den anden række give klynger {a} {b c} {d e} {f}. Skæring efter den tredje række vil give klynger {A} {b c} {d e f}, som er en grovere klyngedannelse, med et færre antal større klynger.
Agglomerativ hierarkisk klyngedannelse
Antag for eksempel, at disse data skal grupperes. Hvor euklidisk afstand er afstandsmetrikken.
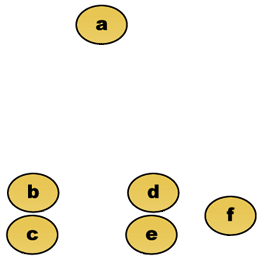
rådata
det hierarkiske klyngedendrogram ville være som sådan:
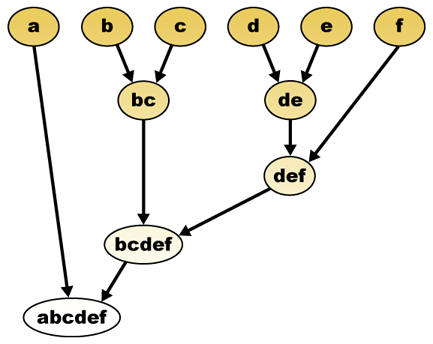
traditionel repræsentation
denne metode bygger hierarkiet ud fra de enkelte elementer ved gradvist at flette klynger. Igen har vi seks elementer {a} {b} {c} {d} {e} og {f}. Det første trin er at bestemme, hvilke elementer der skal fusioneres i en klynge. Normalt vil vi tage de to nærmeste elementer, derfor skal vi definere en afstand 
Antag, at vi har fusioneret de to nærmeste elementer b og c, Vi har nu følgende klynger {A}, {b, c}, {d}, {e} og {f} og ønsker at flette dem yderligere. Men for at gøre det skal vi tage afstanden mellem {A} og {b c} og derfor definere afstanden mellem to klynger. Normalt er afstanden mellem to klynger 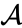
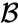
- den maksimale afstand mellem elementer i hver klynge (også kaldet komplet kobling clustering):
- den mindste afstand mellem elementer i hver klynge (også kaldet enkelt kobling clustering):
- den gennemsnitlige afstand mellem elementer i hver klynge (også kaldet gennemsnitlig kobling clustering):
- summen af al intra-cluster varians
- stigningen i varians for klyngen, der flettes (afdelingens kriterium)
- sandsynligheden for, at kandidatklynger gyder fra den samme fordelingsfunktion (V-kobling)
hver agglomerering forekommer i en større afstand mellem klynger end den foregående agglomerering, og man kan beslutte at stoppe klyngedannelse enten når klyngerne er for langt fra hinanden til at blive slået sammen (afstandskriterium), eller når der er et tilstrækkeligt lille antal klynger (talkriterium).
Partitional clustering
k-midler og derivater
K-betyder clustering
k-middelalgoritmen tildeler hvert punkt til klyngen, hvis center (også kaldet centroid) er nærmest. Centret er gennemsnittet af alle punkter i klyngen — det vil sige, dets koordinater er det aritmetiske gennemsnit for hver dimension separat over alle punkter i klyngen.
eksempel: Datasættet har tre dimensioner, og klyngen har to punkter: h = (h1, h2, h3) og Y = (y1, y2, y3). Derefter bliver centroid s = (S1, S2, S3), hvor S1 = (S1 + S1)/2 og S2 = (S2 + s2)/2 og S3 = (S3 + S3)/2.
algoritmen er groft (J. Macron, 1967):
- tilfældigt generere k klynger og bestemme klynge centre, eller direkte generere k frø punkter som klynge Centre.
- tildel hvert punkt til det nærmeste klyngecenter.
- Beregn de nye klyngecentre igen.
- gentag, indtil et konvergenskriterium er opfyldt (normalt at opgaven ikke er ændret).
de vigtigste fordele ved denne algoritme er dens enkelhed og hastighed, som gør det muligt at køre på store datasæt. Dens ulempe er, at det ikke giver det samme resultat med hvert løb, da de resulterende klynger afhænger af de indledende tilfældige opgaver. Det maksimerer variansen mellem klynger (eller minimerer intra-klynge), men sikrer ikke, at resultatet har et globalt minimum af varians.
CLUSTING algoritme
Clustering (Heyer et al., 1999) er en alternativ metode til partitionering af data, opfundet til genklyngning. Det kræver mere computerkraft end k-midler, men kræver ikke at specificere antallet af klynger a priori og returnerer altid det samme resultat, når det køres flere gange.
algoritmen er:
- brugeren vælger en maksimal diameter for klynger.
- Byg en kandidatklynge for hvert punkt ved at inkludere det nærmeste punkt, det næste nærmeste osv., indtil klyngens diameter overstiger tærsklen.
- Gem kandidatklyngen med flest point som den første ægte klynge, og fjern alle punkter i klyngen fra yderligere overvejelse.
- Recurse med det reducerede sæt punkter.
afstanden mellem et punkt og en gruppe punkter beregnes ved hjælp af komplet kobling, dvs. som den maksimale afstand fra punktet til ethvert medlem af gruppen (se afsnittet “Agglomerativ hierarkisk klyngedannelse” om afstand mellem klynger).
uklar c-betyder klyngedannelse
i uklar klyngedannelse har hvert punkt en grad af tilhørsforhold til klynger, som i uklar logik, snarere end at høre helt til kun en klynge. Således kan punkter på kanten af en klynge være i klyngen i mindre grad end punkter i midten af klyngen. For hvert punkt har vi en koefficient, der giver graden af at være i KTH-klyngen 

med uklare C-midler er centroid af en klynge gennemsnittet af alle punkter, vægtet af deres grad af tilhørsforhold til klyngen:
graden af tilhørsforhold er relateret til den inverse af afstanden til klyngen
derefter normaliseres koefficienterne og forvirres med en reel parameter 
for m lig med 2 svarer dette til at normalisere koefficienten lineært for at gøre deres sum 1. Når m er tæt på 1, får klyngecenter tættest på punktet meget mere vægt end de andre, og algoritmen ligner k-midler.
den uklare C-middelalgoritme ligner meget K-middelalgoritmen:
- Vælg et antal klynger.
- Tildel tilfældigt til hvert punkt koefficienter for at være i klyngerne.
- gentag, indtil algoritmen er konvergeret (dvs. koefficienternes ændring mellem to iterationer er ikke mere end
, den givne følsomhedstærskel) :
- Beregn centroid for hver klynge ved hjælp af formlen ovenfor.
- for hvert punkt beregnes dets koefficienter for at være i klyngerne ved hjælp af formlen ovenfor.
algoritmen minimerer også intra-cluster varians, men har de samme problemer som k-midler, minimumet er et lokalt minimum, og resultaterne afhænger af det oprindelige valg af vægte.
Albuekriterium
albuekriteriet er en almindelig tommelfingerregel for at bestemme, hvilket antal klynger der skal vælges, for eksempel til k-midler og agglomerativ hierarkisk klyngedannelse.
albuekriteriet siger, at du skal vælge et antal klynger, så tilføjelse af en anden klynge ikke tilføjer tilstrækkelig information. Mere præcist, hvis du tegner procentdelen af varians forklaret af klyngerne mod antallet af klynger, vil de første klynger tilføje meget information (forklare meget varians), men på et tidspunkt vil den marginale gevinst falde, hvilket giver en vinkel i grafen (albuen).
på den følgende graf er albuen angivet med den røde cirkel. Antallet af valgte klynger bør derfor være 4.
spektral klyngedannelse
i betragtning af et sæt datapunkter kan lighedsmatricen defineres som en matrice 


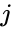
en sådan teknik er shi-Malik-algoritmen, der ofte bruges til billedsegmentering. Det partitioner peger i to sæt 

af 
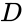
denne partitionering kan udføres på forskellige måder, såsom ved at tage medianen 



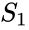
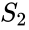
en relateret algoritme er Meila-Shi-algoritmen, som tager egenvektorerne svarende til K største egenværdier af matricen 
applikationer
Biologi
i biologi clustering har mange anvendelser inden for computational biologi og bioinformatik, hvoraf to er:
- i transcriptomics bruges klyngedannelse til at opbygge grupper af gener med relaterede ekspressionsmønstre. Ofte indeholder sådanne grupper funktionelt relaterede proteiner, som f.eks. Eksperimenter med høj kapacitet ved hjælp af udtrykte sekvensmærker (Est ‘ er) eller DNA-mikroarrays kan være et kraftfuldt værktøj til genom-annotation, et generelt aspekt af genomik.
- i sekvensanalyse bruges klyngedannelse til at gruppere homologe sekvenser i genfamilier. Dette er et meget vigtigt begreb inden for bioinformatik og evolutionær biologi generelt. Se evolution ved genduplikation.
Marketing research
klyngeanalyse bruges i vid udstrækning i markedsundersøgelser, når man arbejder med multivariate data fra undersøgelser og testpaneler. Markedsundersøgere bruger klyngeanalyse til at opdele den generelle befolkning af forbrugere i markedssegmenter og bedre forstå forholdet mellem forskellige grupper af forbrugere/potentielle kunder.
- segmentering af markedet og bestemmelse af målmarkeder
- produktpositionering
- ny produktudvikling
- valg af testmarkeder (se : eksperimentelle teknikker)
andre applikationer
Social netværksanalyse: i studiet af sociale netværk kan klyngedannelse bruges til at genkende samfund inden for store grupper af mennesker.
Billedsegmentering: klyngedannelse kan bruges til at opdele et digitalt billede i forskellige regioner til grænsedetektion eller objektgenkendelse.
Data mining: mange data mining-applikationer involverer opdeling af dataelementer i relaterede undergrupper; de marketingapplikationer, der er diskuteret ovenfor, repræsenterer nogle eksempler. En anden almindelig anvendelse er opdeling af dokumenter, såsom verdensomspændende hjemmesider, i genrer.
sammenligninger mellem dataklynger
der har været flere forslag til et mål for lighed mellem to klynger. En sådan foranstaltning kan bruges til at sammenligne, hvor godt forskellige dataklyngealgoritmer udfører på et sæt data. Mange af disse mål er afledt af den matchende matrice (aka forvirringsmatrice), f.eks.
- Jain, Murty og Flynn: data Clustering: en anmeldelse, ACM Comp. Surv., 1999. Tilgængelig her.
- for en anden præsentation af hierarkiske, k-midler og uklare c-midler se denne introduktion til klyngedannelse. Har også en forklaring på blanding af Gaussere.
- David Duve, blanding modellering side – andre klyngedannelse og blanding model links.
- en tutorial om klyngedannelse
- den online lærebog: informationsteori, inferens og læringsalgoritmer, af David J. C. MacKay indeholder kapitler om k-betyder klyngedannelse, blød k-betyder klyngedannelse og afledninger inklusive E-m-algoritmen og variationsvisningen af E-M-algoritmen.
Se også
- k-midler
- kunstigt neuralt netværk (ANN)
- selvorganiserende kort
- Forventningsmaksimering (EM))
bibliografi
- klat værdig, J., Buick, D., Hankins, M., Viinman, J., & Horne, R. (2005). Brug og rapportering af klyngeanalyse i sundhedspsykologi: en gennemgang. Britisk Tidsskrift for Sundhedspsykologi 10: 329-358.
- Romesburg, H. Clarkes, klyngeanalyse for forskere, 2004, 340 s. ISBN 1411606175 eller udgiver, genoptryk af 1990-udgaven udgivet af Krieger Pub. Co… En japansk oversættelse er tilgængelig fra Uchida Rokakuho Publishing Co., Ltd., Tokyo, Japan.
- Heyer, L. J., Kruglyak, S. og Yooseph, S., udforske Ekspressionsdata: identifikation og analyse af Coudtrykte gener, genomforskning 9:1106-1115.
- den online lærebog: informationsteori, inferens og læringsalgoritmer, af David J. C. MacKay inkluderer kapitler om K-betyder klyngedannelse, blød k-betyder klyngedannelse og afledninger inklusive E-m-algoritmen og variationsvisningen af E-M-algoritmen.
til spektral klyngedannelse :
- Jianbo Shi og Jitendra Malik, “normaliserede snit og Billedsegmentering”, IEEE-transaktioner på mønsteranalyse og Maskinintelligens, 22(8), 888-905, August 2000. Tilgængelig på Jitendra Maliks hjemmeside
- Marina Meila og Jianbo Shi, “Læringssegmentering med tilfældig gåtur”, neurale informationsbehandlingssystemer, NIPS, 2001. Tilgængelig fra Jianbo Shis hjemmeside
til estimering af antal klynger:
- Can, F., Oskarahan, E. A. (1990) ” begreber og effektivitet af den dækningskoefficientbaserede klyngemetode for tekstdatabaser.”ACM-transaktioner på databasesystemer. 15 (4) 483-517.
programmel implementeringer
gratis
- fleksklust-pakken til R
- YALE (endnu et læringsmiljø): gratis open source – program til videnopdagelse og datamining, herunder også et plugin til klyngedannelse
- nogle Matlab-kildefiler til klyngedannelse her
- kompakt-sammenlignende pakke til klyngevurdering (også i Matlab)
- Blandingsmod : Model Baseret Klynge Og Diskriminant Analyse. Kode i C++, interface med Matlab og Scilab
- LingPipe Clustering Tutorial Tutorial til at gøre komplet – og single-link clustering hjælp LingPipe, en Java tekst data mining pakke distribueret med kilde.
- Vika : Vika indeholder værktøjer til databehandling, klassificering, regression, klyngedannelse, associeringsregler og visualisering. Det er også velegnet til udvikling af nye maskinindlæringsordninger.