i dag vil være en kort introduktion til cirkulær statistik (undertiden benævnt retningsbestemt statistik). Cirkulær statistik er en interessant underopdeling af statistikker, der involverer observationer taget som vektorer omkring en enhedscirkel. Forestil dig for eksempel at måle fødselstider på et hospital over en 24-timers cyklus eller retningsdispersionen af en gruppe vandrende dyr. Denne type data er involveret i en række områder, såsom økologi, klimatologi og biokemi. Arten af måling af observationer omkring en enhedscirkel nødvendiggør en anden tilgang til hypotesetest. Distributioner skal “vikles” rundt om cirklen for at være til brug, og konventionelle estimatorer som f.eks prøve gennemsnit eller prøvevarians holder intet vand.
i dette indlæg vil vi gennemføre Raos Afstandstest for at vurdere ensartetheden af et cirkulært datasæt. Dette er en grundlæggende procedure og bør betragtes som en introduktion til håndtering af cirkulære data.
Kom godt i gang
vi skal gennemføre en hypotesetest på skildpadder, et lille datasæt bestående af ankomstvinklerne på 10 grønne havskildpadder til deres hekkeø. Vores mål er at bestemme, hvor ankomstvinklerne viser tegn på retningsbestemmelse eller er mere vejledende for en tilfældig spredning.
først skal du installere circular pakken og vedhæfte turtles datasættet.
install.packages("circular")require(circular)attach(turtles)
plotte dataene
circular pakken indeholder sin egen plottefunktion, plot.circular. Lad os observere skildpaddernes ankomstvinkler.
plot.circular(arrival)
her er plottet: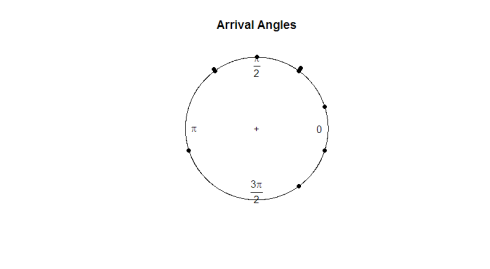
i betragtning af øjetesten ser observationerne ud til at være ensartede rundt om cirklen. Hvis vi ønsker at køre en hypotesetest for at afgøre, om dataene virkelig er ensartede, bliver vi nødt til at udvikle en teststatistik, der fungerer med vinkeldata.
Hvad er en god parameter for os at udnytte? At tage prøven betyder ikke meget om retningen af dataene (180 grader er ikke et nyttigt gennemsnit på 2 grader og 358 grader). I det følgende plot skal du observere, hvordan prøvegennemsnittet ikke nytter at repræsentere formen eller spredningen af vores data.
mean(arrival)plot.circular(mean(arrival)) 0.9120794
her er plottet: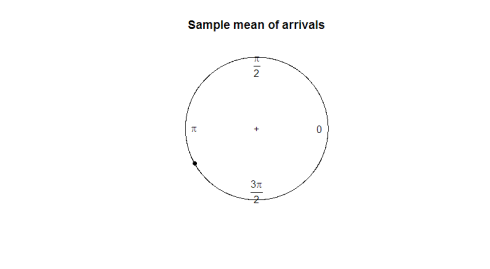
i stedet bruger vi en metode, der bestemmer retningsbestemmelse ved at måle det gennemsnitlige mellemrum mellem observationer. Denne test kaldes Raos Afstandstest.
Raos Afstandstest
Raos Afstandstest blev udviklet til at vurdere ensartetheden af cirkulære data. Det bruger mellemrummet mellem observationer til at bestemme, om dataene viser betydelig retningsbestemmelse. Hvis dataene er ensartede, skal observationer have en tendens til at være jævnt fordelt fra hinanden.
her er teststatistikken \(U\) til Raos Afstandstest: $ $ U = 1/2 \ sum \ limits_{i=1}^n / t_{i} – Larv / $ $ hvor \(Larv = 360 / n, T_{i} = f_{i + 1} – f_{i}\) og \(T_{N} = (360-F_{n}) + f_{1}\)
grundlæggende aggregerer teststatistikken afvigelserne mellem på hinanden følgende punkter, hver vægtet med det samlede antal observationer i datasættet.
vi bruger funktionen rao.spacing.test() til at køre denne hypotesetest. Vores nulhypotese siger, at dataene har en ensartet fordeling, mens alternativet angiver, at dataene viser tegn på retningsbestemmelse. Lad os køre testen.
rao.spacing.test(arrival,alpha=.10) Rao's Spacing Test of Uniformity Test Statistic = 127.2689 Level 0.1 critical value = 161.23 Do not reject null hypothesis of uniformity
med en teststatistik på 127, der falder under den kritiske værdi på 161, undlader dataene at læne sig markant i nogen retning. Vi kan ikke afvise hypotesen om, at skildpaddernes ankomster har en ensartet fordeling.
konklusion
Raos afstandstest bestemte dataene til ikke at vise tegn på retningstendenser. Vi kan ikke afvise nulhypotesen om ensartethed og vil antage ensartethed med hensyn til ankomstretningen. Mens dette indlæg var en relativt grundlæggende tutorial, har mange mennesker i datavidenskabssamfundet ikke arbejdet med cirkulære data før. Det er et interessant underemne at dykke ind i såvel som et ungt statistikfelt, der stadig udvikler sig.
afsluttende bemærkninger
jeg vil gerne udvide kredit til S. Rao Jammalamadaka ph.d., fra University of California, Santa Barbara, og hans lærebog “emner i cirkulær statistik” for at udløse min interesse inden for cirkulær statistik.