4.2 estimering af koefficienterne for den lineære regressionsmodel / Introduktion til økonometri med R

4.2 estimering af koefficienterne for den lineære regressionsmodel

i praksis er aflytningen $\beta_0$ og hældningen $\beta_1$ af befolkningsregressionslinjen ukendt. Derfor skal vi anvende data til at estimere begge ukendte parametre. I det følgende vil et virkeligt verdenseksempel blive brugt til at demonstrere, hvordan dette opnås. Vi ønsker at relatere testresultater til elev-lærerforhold målt i californiske skoler. Testresultatet er det distriktsdækkende gennemsnit af læse-og matematikresultater for femte klassinger. Igen måles klassestørrelsen som antallet af studerende divideret med antallet af lærere (forholdet mellem studerende og lærer). Hvad angår dataene, leveres California School data set (CASchools) med en R-pakke kaldet AER, et akronym for Anvendt økonometri med R (Kleiber og tid 2020). Efter installation af pakken med installation.pakker (“AER”) og vedhæfte det med bibliotek(AER) datasættet kan indlæses ved hjælp af funktionen data ().

## # install the AER package (once)## install.packages("AER")## ## # load the AER packagelibrary(AER)# load the the data set in the workspacedata(CASchools)

når en pakke er installeret, er den tilgængelig til brug ved yderligere lejligheder, når den påberåbes med bibliotek() — der er ingen grund til at køre installation.pakker () igen!

det er interessant at vide, hvilken slags objekt vi har at gøre med.klasse () returnerer klassen af et objekt. Afhængigt af klassen af et objekt opfører nogle funktioner (for eksempel plot () og Resume ()) forskelligt.

lad os kontrollere klassen af objektet CASchools.

class(CASchools)#> "data.frame"

det viser sig, at CASchools er af klassedata.ramme, som er et praktisk format at arbejde med, især til udførelse af regressionsanalyse.

ved hjælp af head() får vi et første overblik over vores data. Denne funktion viser kun de første 6 rækker af datasættet, som forhindrer en overfyldt konsoludgang.

tryk på ctrl + L for at rydde konsollen. Denne kommando sletter enhver kode, der er indtastet og udført af dig eller udskrevet til konsollen af R-funktioner. Den gode nyhed er, at alt andet er uberørt. Du hverken løs definerede variabler etc. heller ikke kodehistorikken. Det er stadig muligt at huske tidligere udførte r-kommandoer ved hjælp af op-og ned-tasterne. Hvis du arbejder i RStudio, skal du trykke på ctrl + op på tastaturet (CMD + op på en Mac) for at gennemgå en liste over tidligere indtastede kommandoer.

head(CASchools)#> district school county grades students teachers#> 1 75119 Sunol Glen Unified Alameda KK-08 195 10.90#> 2 61499 Manzanita Elementary Butte KK-08 240 11.15#> 3 61549 Thermalito Union Elementary Butte KK-08 1550 82.90#> 4 61457 Golden Feather Union Elementary Butte KK-08 243 14.00#> 5 61523 Palermo Union Elementary Butte KK-08 1335 71.50#> 6 62042 Burrel Union Elementary Fresno KK-08 137 6.40#> calworks lunch computer expenditure income english read math#> 1 0.5102 2.0408 67 6384.911 22.690001 0.000000 691.6 690.0#> 2 15.4167 47.9167 101 5099.381 9.824000 4.583333 660.5 661.9#> 3 55.0323 76.3226 169 5501.955 8.978000 30.000002 636.3 650.9#> 4 36.4754 77.0492 85 7101.831 8.978000 0.000000 651.9 643.5#> 5 33.1086 78.4270 171 5235.988 9.080333 13.857677 641.8 639.9#> 6 12.3188 86.9565 25 5580.147 10.415000 12.408759 605.7 605.4

vi finder ud af, at datasættet består af masser af variabler, og at de fleste af dem er numeriske.

forresten: et alternativ til klasse() og hoved() er str (), som er udledt af ‘struktur’ og giver et omfattende overblik over objektet. Prøv!

vender tilbage til CASchools, de to variabler, vi er interesseret i (dvs., gennemsnitlig test score og forholdet mellem studerende og lærer) er ikke inkluderet. Det er dog muligt at beregne begge ud fra de angivne data. For at opnå forholdet mellem studerende og lærer deler vi simpelthen antallet af studerende med antallet af lærere. Den gennemsnitlige test score er det aritmetiske gennemsnit af test score for læsning og score for matematik test. Den næste kodestykke viser, hvordan de to variabler kan konstrueres som vektorer, og hvordan de føjes til CASchools.

# compute STR and append it to CASchoolsCASchools$STR <- CASchools$students/CASchools$teachers # compute TestScore and append it to CASchoolsCASchools$score <- (CASchools$read + CASchools$math)/2

hvis vi løb hoved(CASchools) igen, ville vi finde de to variabler af interesse som yderligere kolonner med navnet STR og score (Tjek dette!).

tabel 4.1 fra lærebogen opsummerer fordelingen af testresultater og elev-lærerforhold. Der er flere funktioner, der kan bruges til at producere lignende resultater, f. eks.,

gennemsnit () (beregner det aritmetiske gennemsnit af de angivne tal),
sd () (beregner prøvestandardafvigelsen),
kvantile () (returnerer en vektor af de angivne prøvekvantiler for dataene).

den næste kodestykke viser, hvordan man opnår dette. Først beregner vi sammenfattende statistikker om kolonnerne STR og score for CASchools. For at få flot output samler vi foranstaltningerne i en data.ramme med navnet DistributionSummary.

# compute sample averages of STR and scoreavg_STR <- mean(CASchools$STR) avg_score <- mean(CASchools$score)# compute sample standard deviations of STR and scoresd_STR <- sd(CASchools$STR) sd_score <- sd(CASchools$score)# set up a vector of percentiles and compute the quantiles quantiles <- c(0.10, 0.25, 0.4, 0.5, 0.6, 0.75, 0.9)quant_STR <- quantile(CASchools$STR, quantiles)quant_score <- quantile(CASchools$score, quantiles)# gather everything in a data.frame DistributionSummary <- data.frame(Average = c(avg_STR, avg_score), StandardDeviation = c(sd_STR, sd_score), quantile = rbind(quant_STR, quant_score))# print the summary to the consoleDistributionSummary#> Average StandardDeviation quantile.10. quantile.25. quantile.40.#> quant_STR 19.64043 1.891812 17.3486 18.58236 19.26618#> quant_score 654.15655 19.053347 630.3950 640.05000 649.06999#> quantile.50. quantile.60. quantile.75. quantile.90.#> quant_STR 19.72321 20.0783 20.87181 21.86741#> quant_score 654.45000 659.4000 666.66249 678.85999

hvad angår prøvedataene, bruger vi plot (). Dette giver os mulighed for at registrere egenskaber ved vores data, såsom outliers, som er sværere at opdage ved at se på blotte tal. Denne gang tilføjer vi nogle yderligere argumenter til Call of plot().

det første argument i vores call of plot(), score ~ STR, er igen en formel, der angiver variabler på Y-og H-aksen. Denne gang gemmes de to variabler imidlertid ikke i separate vektorer, men er kolonner af CASchools. Derfor ville R ikke finde dem uden at argumentdataene er korrekt specificeret. data skal være i overensstemmelse med navnet på dataene.ramme, som variablerne tilhører, i dette tilfælde CASchools. Yderligere argumenter bruges til at ændre plottets udseende: mens main tilføjer en titel, tilføjer ylab og ylab brugerdefinerede etiketter til begge akser.

plot(score ~ STR, data = CASchools, main = "Scatterplot of TestScore and STR", xlab = "STR (X)", ylab = "Test Score (Y)")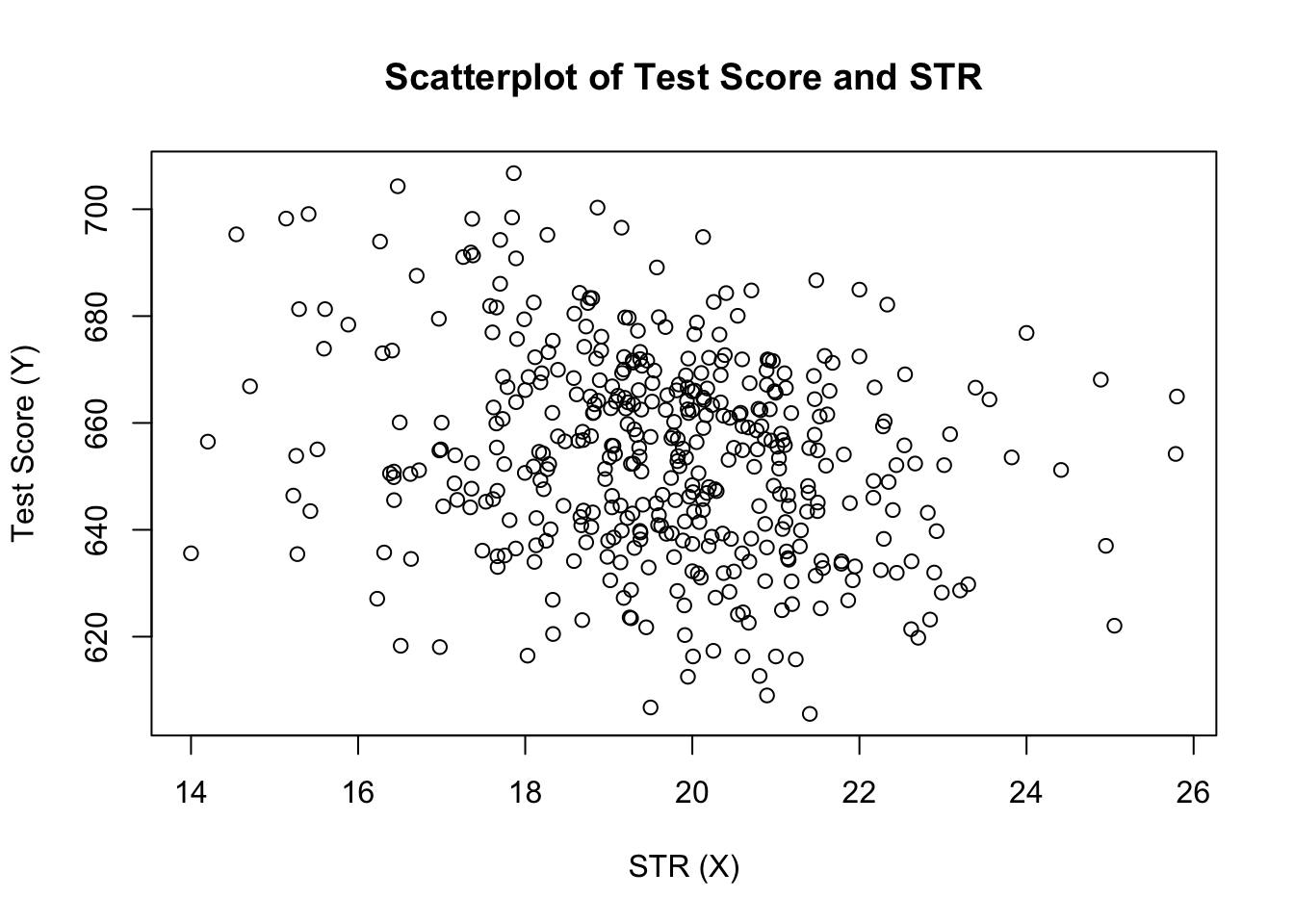

grunden (figur 4.2 i bogen) viser spredningenplot af alle observationer om elev-lærer-forholdet og testresultatet. Vi ser, at punkterne er stærkt spredte, og at variablerne er negativt korrelerede. Det vil sige, vi forventer at observere lavere testresultater i større klasser.

funktionen cor() (se ?cor for yderligere info) kan bruges til at beregne korrelationen mellem to numeriske vektorer.

cor(CASchools$STR, CASchools$score)#> -0.2263627

som scatterplot allerede antyder, er korrelationen negativ, men ret svag.

den opgave, vi nu står over for, er at finde en linje, der bedst passer til dataene. Selvfølgelig kunne vi simpelthen holde fast i grafisk inspektion og korrelationsanalyse og derefter vælge den bedste passende linje ved at eyeballing. Dette ville imidlertid være temmelig subjektivt: forskellige observatører ville tegne forskellige regressionslinjer. På denne konto er vi interesserede i teknikker, der er mindre vilkårlige. En sådan teknik er givet ved almindelig mindste kvadrater (OLS) estimering.

den almindelige mindste kvadraters Estimator

OLS-estimatoren vælger regressionskoefficienterne således, at den estimerede regressionslinje er så “tæt” som muligt på de observerede datapunkter. Her måles nærhed ved summen af de kvadratiske fejl, der er gjort ved at forudsige $Y$ givet $h$. Lad $b_0$ og $b_1$ være nogle estimatorer af $\beta_0$ og $\beta_1$. Derefter kan summen af kvadrerede estimeringsfejl udtrykkes som

OLS-estimatoren i den enkle regressionsmodel er parret af estimatorer til aflytning og hældning, hvilket minimerer udtrykket ovenfor. Afledningen af OLS-estimatorerne for begge parametre er præsenteret i bilag 4.1 til bogen. Resultaterne er opsummeret i Key Concept 4.2.

OLS-estimatoren, forudsagte værdier og rester

OLS-estimatorerne for hældningen $\beta_1$ og skæringspunktet $\beta_0$ i den enkle lineære regressionsmodel er\OLS-forudsagte værdier $\bredhat{Y}_i$ og rester $\hat{u}_i$ er\

det estimerede skæringspunkt $\hat{\beta}_0$, hældningsparameteren $\hat{\beta}_1$ og residualerne $\Left(\Hat{U}_i\right)$ beregnes ud fra en prøve af $N$ observationer af $h_i$ og $y_i$, $i$, $…$, $og$. Dette er estimater af den ukendte population intercept $\left (\beta_0\ right)$, slope $\left (\beta_1\ right)$ og error term$(u_i)$.

formlerne præsenteret ovenfor er muligvis ikke særlig intuitive ved første øjekast. Følgende interaktive program har til formål at hjælpe dig med at forstå mekanikken i OLS. Du kan tilføje observationer ved at klikke på koordinatsystemet, hvor dataene er repræsenteret af punkter. Når to eller flere observationer er tilgængelige, beregner applikationen en regressionslinje ved hjælp af OLS og nogle statistikker, der vises i højre panel. Resultaterne opdateres, når du tilføjer yderligere observationer til venstre panel. Et dobbeltklik nulstiller applikationen, dvs.alle data fjernes.

der er mange mulige måder at beregne $\hat{\beta}_0$ og $\hat{\beta}_1$ i R. For eksempel kunne vi implementere formlerne præsenteret i nøglekoncept 4.2 med to af R ‘ s mest basale funktioner: middelværdi() og sum(). Før vi gør det, vedhæfter vi CASchools datasættet.

attach(CASchools) # allows to use the variables contained in CASchools directly# compute beta_1_hatbeta_1 <- sum((STR - mean(STR)) * (score - mean(score))) / sum((STR - mean(STR))^2)# compute beta_0_hatbeta_0 <- mean(score) - beta_1 * mean(STR)# print the results to the consolebeta_1#> -2.279808beta_0#> 698.9329

Calling attach (CASchools) gør det muligt for os at adressere en variabel indeholdt i CASchools ved navn: det er ikke længere nødvendigt at bruge $ – operatøren sammen med datasættet: R kan evaluere variabelnavnet direkte.

R bruger objektet i brugermiljøet, hvis dette objekt deler navnet på variablen indeholdt i en vedhæftet database. Det er dog en bedre praksis at altid bruge karakteristiske navne for at undgå sådanne (tilsyneladende) ambivalenser!

Bemærk, at vi adresserer variabler indeholdt i de vedhæftede datasæt CASchools direkte for resten af dette kapitel!

selvfølgelig er der endnu flere manuelle måder at udføre disse opgaver på. Da OLS er en af de mest anvendte estimeringsteknikker, indeholder R selvfølgelig allerede en indbygget funktion ved navn lm() (lineær model), som kan bruges til at udføre regressionsanalyse.

det første argument for den funktion, der skal specificeres, er, svarende til plot (), regressionsformlen med den grundlæggende syntaks y ~ hvor y er den afhængige variabel og den forklarende variabel. Argumentdataene bestemmer det datasæt, der skal bruges i regressionen. Vi gennemgår nu eksemplet fra bogen, hvor forholdet mellem testresultaterne og klassestørrelserne analyseres. Følgende kode bruger lm () til at replikere resultaterne præsenteret i figur 4.3 i bogen.

# estimate the model and assign the result to linear_modellinear_model <- lm(score ~ STR, data = CASchools)# print the standard output of the estimated lm object to the console linear_model#> #> Call:#> lm(formula = score ~ STR, data = CASchools)#> #> Coefficients:#> (Intercept) STR #> 698.93 -2.28

lad os tilføje den estimerede regressionslinje til plottet. Denne gang udvider vi også områderne for begge akser ved at indstille argumenterne.

# plot the dataplot(score ~ STR, data = CASchools, main = "Scatterplot of TestScore and STR", xlab = "STR (X)", ylab = "Test Score (Y)", xlim = c(10, 30), ylim = c(600, 720))# add the regression lineabline(linear_model)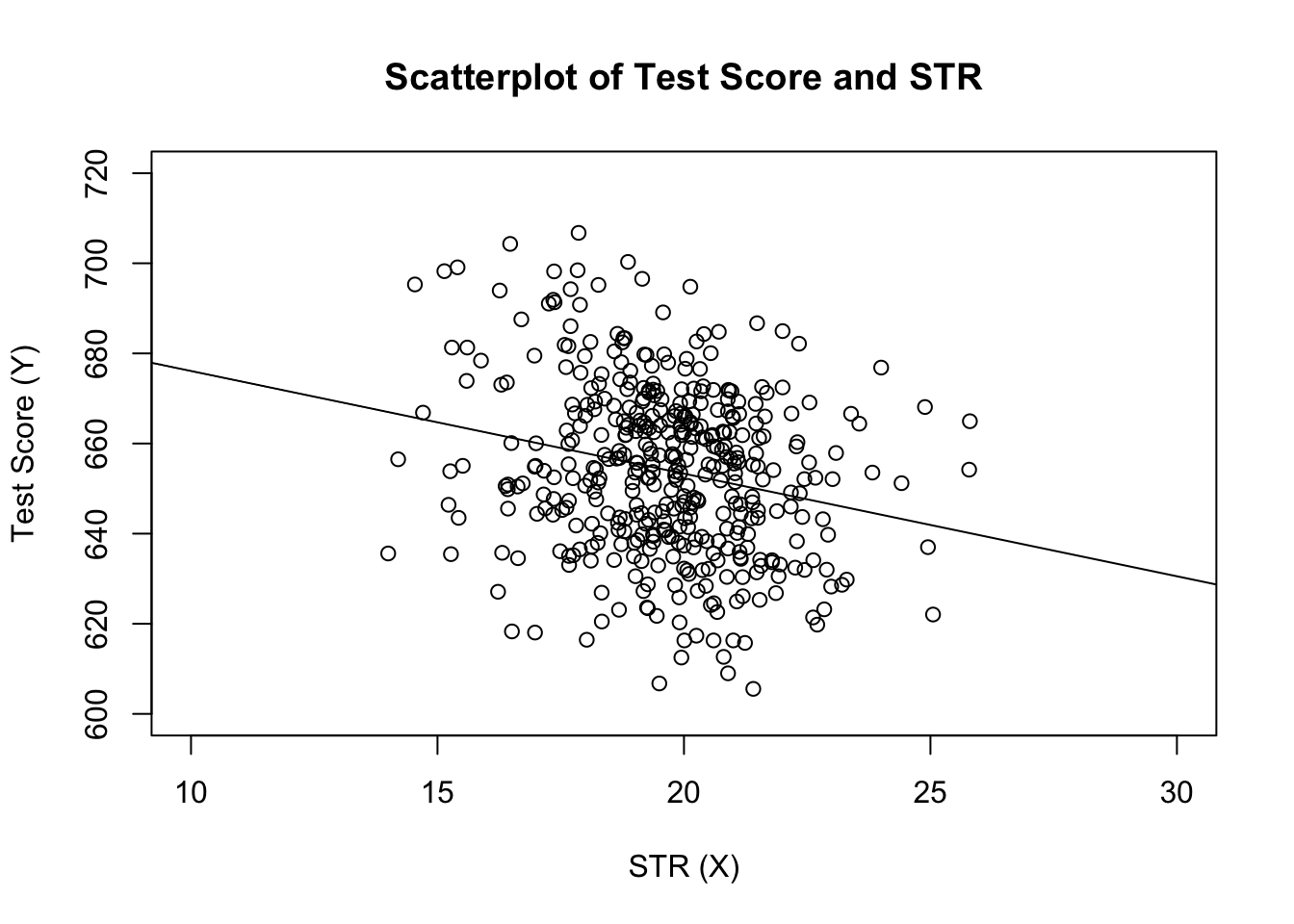

har du bemærket, at denne gang passerede vi ikke intercept-og hældningsparametrene til abline? Hvis du kalder abline () på et objekt i klasse lm, som kun indeholder en enkelt regressor, trækker R regressionslinjen automatisk!