antaget viden
studerende vil have haft omfattende uformel erfaring med geometri i tidligere år, og dette vil give et godt intuitivt grundlag for den mere systematiske tilgang til geometri passende i år 7-10. De særlige emner fra år F−6, der er relevante for dette modul, er:
- brug af kompasser og linealer og omhyggelig tegning af geometriske figurer.
- typer af vinkler, herunder mindst rette vinkler, akutte vinkler, stumpe vinkler og
refleksvinkler. - trekanter, herunder en uformel introduktion til ligebenede og ligesidede trekanter.
- firkanter, herunder en uformel introduktion til firkanter, rektangler, parallelogrammer, trapeser og rhombusser.
- uformel erfaring med oversættelser, refleksioner, rotationer og udvidelser,
og med symmetri i forbindelse med aktiviteter som foldning af en ensartet trekant, rektangel eller rhombus.
Motivation
 geometri bruges til at modellere verden omkring os. En visning af tagene på huse afslører trekanter, trapeser og rektangler, mens flisemønstre i fortove og badeværelser bruger sekskanter, femkanter, trekanter og firkanter.
geometri bruges til at modellere verden omkring os. En visning af tagene på huse afslører trekanter, trapeser og rektangler, mens flisemønstre i fortove og badeværelser bruger sekskanter, femkanter, trekanter og firkanter.
bygherrer, fliser, arkitekter, grafiske designere og netdesignere bruger rutinemæssigt geometriske ideer i deres arbejde. Det er meget vigtigt at klassificere sådanne geometriske objekter og studere deres egenskaber. Geometri har også mange anvendelser inden for kunst.
ligesom aritmetik har tal som sine grundlæggende studieobjekter, så er punkter, linjer og cirkler de grundlæggende byggesten i plangeometri.
i gymnasiets geometri begynder vi med en række intuitive ideer (punkter, linjer og vinkler), som slet ikke er lette at præcist definere, efterfulgt af nogle definitioner (lodret modsatte vinkler, parallelle linjer osv.), og ud fra disse udleder vi vigtige fakta, der ofte omtales som sætninger. I gymnasiet bør strengheden udvikle sig langsomt fra det ene år til det næste, men på hvert trin er det meget vigtigt og bør understreges.
geometri giver således eleverne mulighed for at udvikle deres geometriske intuition, som har anvendelser på mange områder af livet, og også at lære at konstruere logiske argumenter og foretage fradrag i en indstilling, der for det meste er uafhængig
af nummer.
indhold
punkter og linjer
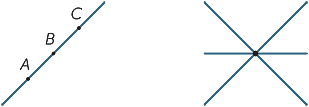
de enkleste objekter i plangeometri er punkter og linjer. Fordi de er så enkle, det er svært at give præcise definitioner af dem, så i stedet sigter vi mod at give eleverne en grov beskrivelse af deres egenskaber, der er i tråd med vores intuition. Et punkt markerer en position, men har ingen størrelse. I praksis, når vi tegner et punkt, har det klart en bestemt bredde, men det repræsenterer et punkt i vores fantasi. En linje har ingen bredde og strækker sig uendeligt i begge retninger. Når vi tegner en linje, har den bredde, og den har ender, så det er ikke rigtig en linje, men repræsenterer en linje i vores fantasi. Givet to forskellige punkter A og B, så er der en (og kun en) linje, der passerer gennem begge punkter. Vi bruger store bogstaver til at henvise til punkter og navnelinjer enten ved at angive to punkter på linjen eller ved at bruge små bogstaver som  og m. således betegnes den givne linje nedenfor som linjen AB eller som linjen
og m. således betegnes den givne linje nedenfor som linjen AB eller som linjen  .
.

givet to forskellige linjer er der to muligheder: de kan enten mødes på et enkelt punkt, eller de mødes måske aldrig, uanset hvor langt de udvides (eller produceres). Linjer, der aldrig mødes, kaldes parallelle. I det andet diagram skriver vi AB ||CD.
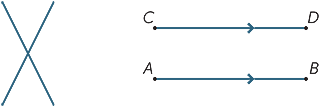
tre (eller flere) punkter, der ligger på en lige linje, kaldes collinear.
tre (eller flere) linjer, der mødes på et enkelt punkt kaldes samtidig.
|
|
|
| Collinear |
samtidig |
øvelse 1
tegn tre linjer, der ikke er samtidige, således at ingen to er parallelle.
Øvelse 2
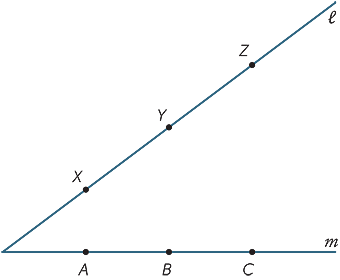
lav en stor kopi af nedenstående diagram. Punkterne er alle punkter på linjen  og A, B, C er alle punkter på linjen m. Deltag i AY og B kalder deres kryds R. Deltag i BS og YC og kalder deres kryds P. Deltag i KS OG Å og kalder deres kryds spørgsmål. Hvad bemærker du om punkterne P, K, R? (Dette resultat kaldes Pappus ‘ sætning, c. 340 e. kr.)
og A, B, C er alle punkter på linjen m. Deltag i AY og B kalder deres kryds R. Deltag i BS og YC og kalder deres kryds P. Deltag i KS OG Å og kalder deres kryds spørgsmål. Hvad bemærker du om punkterne P, K, R? (Dette resultat kaldes Pappus ‘ sætning, c. 340 e. kr.)
intervaller, stråler og vinkler
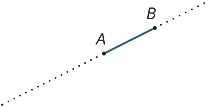 Antag, at A og B er to punkter på en linje. Intervallet
Antag, at A og B er to punkter på en linje. Intervallet
AB er den del af linjen mellem A og B, inklusive de to endepunkter.
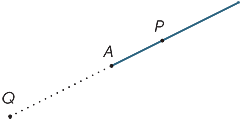 punktet A i diagrammet deler linjen i to stykker kaldet stråler. Ray AP er den stråle, der indeholder punktet P (og punktet A).
punktet A i diagrammet deler linjen i to stykker kaldet stråler. Ray AP er den stråle, der indeholder punktet P (og punktet A).
Vinkler
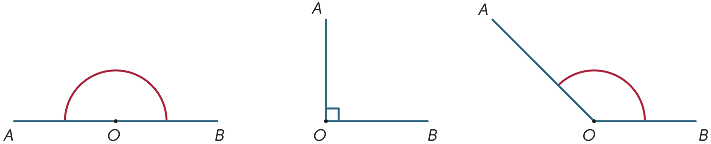
 i diagrammet kaldes det skraverede område mellem strålerne OA og OB vinklen AOB eller vinklen BOA. Vinkelskiltet
i diagrammet kaldes det skraverede område mellem strålerne OA og OB vinklen AOB eller vinklen BOA. Vinkelskiltet ![]() er skrevet, så vi skriver
er skrevet, så vi skriver ![]() AOB.
AOB.
 det skraverede område udenfor kaldes refleksvinklen dannet af OA og OB. Det meste af tiden, medmindre vi angiver ordet refleks, henviser alle vores vinkler til området mellem strålerne og ikke uden for dem.
det skraverede område udenfor kaldes refleksvinklen dannet af OA og OB. Det meste af tiden, medmindre vi angiver ordet refleks, henviser alle vores vinkler til området mellem strålerne og ikke uden for dem.
størrelsen af en vinkel
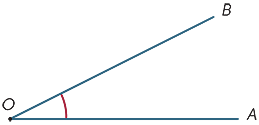 Forestil dig, at strålen OB roteres omkring punktet O, indtil den ligger langs OA. Mængden af drejning kaldes størrelsen af vinklen AOB. Vi kan ligeledes definere størrelsen af refleksvinklen.
Forestil dig, at strålen OB roteres omkring punktet O, indtil den ligger langs OA. Mængden af drejning kaldes størrelsen af vinklen AOB. Vi kan ligeledes definere størrelsen af refleksvinklen.
vi vil ofte bruge små græske bogstaver,,,,,,… at repræsentere størrelsen af en vinkel.
størrelsen af vinklen svarende til en fuld revolution blev opdelt (af babylonierne) i 360 lige store dele, som vi kalder grader. (De valgte sandsynligvis 360, da det var tæt på antallet af dage om året.) Derfor er størrelsen af en retvinkel 180 liter og størrelsen af en retvinkel er 90 liter. Andre vinkler kan måles (ca.) ved hjælp af en grader.
|
|
||
| lige vinkel | højre vinkel |
stump vinkel |
vinkler klassificeres efter deres størrelse. Vi siger, at en vinkel med størrelsen α er akut
(et ord, der betyder ‘skarpe’) hvis 0° < α < 90°, a er stump (et ord, der betyder ‘stump’) hvis
90° < α < 180°, og α er en refleks, hvis 180° < α < 360°.
da graden har to skalaer, skal eleverne være forsigtige, når de tegner og
måler vinkler. Det er en god øvelse at bruge en grader til at tegne nogle vinkler som 30°, 78°, 130°, 163°.
Øvelse 3
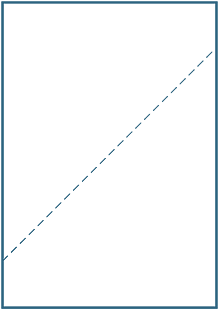 Fold et A4-ark papir, der matcher de (diagonalt) modsatte hjørner. Tegn en linje langs den krølle, der er dannet, og mål vinklerne mellem folden og siden.
Fold et A4-ark papir, der matcher de (diagonalt) modsatte hjørner. Tegn en linje langs den krølle, der er dannet, og mål vinklerne mellem folden og siden.
i øvelsen ovenfor danner de to vinkler sammen en lige linje og tilføjer således til 180 liter. To vinkler, der føjer til 180 kr., kaldes supplerende vinkler; således er 45 kr.og 135 kr. supplerende vinkler.
to vinkler, der føjer til 90 kr., kaldes komplementære; således er 23 kr. og 67 kr.
komplementære vinkler.
vinkler på et punkt
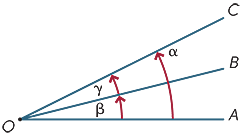 to vinkler på et punkt siges at være tilstødende, hvis de deler en fælles stråle. Derfor er
to vinkler på et punkt siges at være tilstødende, hvis de deler en fælles stråle. Derfor er ![]() AOB og
AOB og ![]() BOC i diagrammet tilstødende.
BOC i diagrammet tilstødende.
tilstødende vinkler kan tilføjes, så i diagrammet
lyri = lyri + lyri.
når to linjer skærer hinanden, dannes fire vinkler ved skæringspunktet.
i diagrammet kaldes vinklerne markeret ![]() AOKS og
AOKS og ![]() dreng lodret modsat.
dreng lodret modsat.
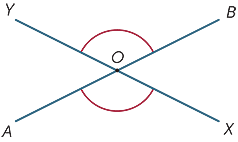 siden
siden
-
 AOKS er tillægget til
AOKS er tillægget til  boks (lige vinkel).
boks (lige vinkel). -
 dreng er også supplement til
dreng er også supplement til  kasse (lige vinkel),
kasse (lige vinkel),
vi kan konkludere, at disse lodret modsatte vinkler, ![]() AOKS og
AOKS og ![]() dreng er ens. Vi har således vores første
dreng er ens. Vi har således vores første
vigtige geometriske udsagn:
lodret modsatte vinkler er ens.
et resultat i geometri (og i matematik generelt) kaldes ofte en sætning. En sætning er en vigtig erklæring, som kan bevises ved logisk fradrag. Argumentet ovenfor er et bevis på sætningen; undertiden præsenteres beviser formelt efter sætningen.
 hvis to linjer skærer hinanden, så alle fire vinkler er retvinkler, siges linjerne at være vinkelret.
hvis to linjer skærer hinanden, så alle fire vinkler er retvinkler, siges linjerne at være vinkelret.
vinkler ved et punkt-geometriske argumenter
følgende grunde kan bruges i geometriske argumenter:
- tilstødende vinkler kan tilføjes eller trækkes fra.
- vinkler i en revolution tilføje til 360 kr.
- vinkler i en lige linje tilføje til 180 liter.
- lodret modsatte vinkler er ens.
tværgående og parallelle linjer
 en tværgående er en linje, der møder to andre linjer.
en tværgående er en linje, der møder to andre linjer.
tilsvarende vinkler
forskellige vinkler dannes af tværgående. I diagrammerne nedenfor kaldes de to markerede vinkler tilsvarende vinkler.
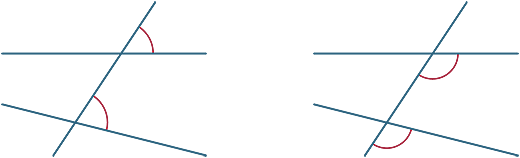
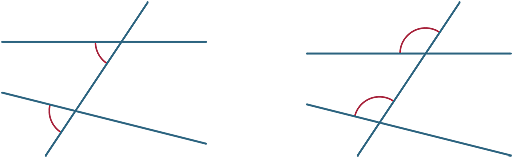
 vi ser nu på, hvad der sker, når de to linjer, der skæres af tværgående, er parallelle.
vi ser nu på, hvad der sker, når de to linjer, der skæres af tværgående, er parallelle.
Inituitively, hvis vinklen α var større end β derefter CD-ville krydse AB til venstre for F, og hvis den var mindre end β, det ville kryds til højre for F. da linjerne ikke kryds ved alle, α kan hverken være mindre eller mere end β og så er lig med β.
alternativt kan du forestille dig at oversætte vinklen KGD langs GF, indtil G falder sammen med F. da linjerne er parallelle, ville vi forvente, at vinklen kr ville falde sammen med vinklen KRR. Denne observation fører os til formodning om, at:
tilsvarende vinkler dannet af parallelle linjer er ens.
vi kan ikke bevise dette resultat, selvom vi har vist, at det er geometrisk plausibelt. Vi vil acceptere det som et aksiom af geometri. Et aksiom er en erklæring, som vi ikke kan bevise, men som er intuitivt rimelig. Bemærk, at mange af de kendsgerninger, vi allerede har nævnt, såsom: tilstødende vinkler kan tilføjes, og to punkter bestemmer en linje osv., er også aksiomer, selvom vi ikke udtrykkeligt har angivet dem på denne måde.
Alternative vinkler
i hvert diagram kaldes de to markerede vinkler alternative vinkler (da de er på alternative sider af tværgående).

 hvis linjerne AB og CD er parallelle, er de alternative vinkler ens. Dette resultat kan nu bevises.
hvis linjerne AB og CD er parallelle, er de alternative vinkler ens. Dette resultat kan nu bevises.
![]() DGK = ret (tilsvarende vinkler, AB / / CD)
DGK = ret (tilsvarende vinkler, AB / / CD)
![]() (vertikalt modsatte vinkler ved G)
(vertikalt modsatte vinkler ved G)
så lussing = lussing.
for at opsummere:
Alternative vinkler dannet af parallelle linjer er ens.
Co-indvendige vinkler
endelig kaldes de to markerede vinkler i hvert diagram nedenfor co-indvendige vinkler og ligger på samme side af tværgående.

hvis linjerne AB og CD er parallelle, er det indlysende, at de co-indvendige vinkler ikke er ens, men det viser sig, at de er supplerende, det vil sige deres sum er 180 liter .
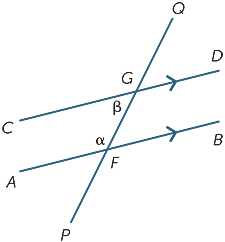 dette er et resultat, som også er let at bevise:
dette er et resultat, som også er let at bevise:
![]() BFG = liter (alternative vinkler, AB ||CD)
BFG = liter (alternative vinkler, AB ||CD)
liter + liter = 180 liter (lige vinkel ved F)
for at opsummere:
Co-indvendige vinkler dannet af parallelle linjer er supplerende.
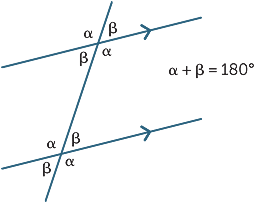 de tre resultater kan opsummeres
de tre resultater kan opsummeres
ved følgende diagram:
numeriske eksempler
givet information om vinklerne i et diagram, kan vi bruge ovenstående resultater til at finde størrelsen på andre vinkler i diagrammet. Dette er en enkel, men meget vigtig færdighed, ofte omtalt uformelt som vinkeljagt. Ved løsning af problemer er rækkefølgen af trin ikke altid unik. Der kan være flere forskellige, men lige så gyldige tilgange.
for eksempel søger vi i det følgende diagram størrelsen af vinkel BAC.

![]() DCA = 102 liter (alternative vinkler, AC / BD)
DCA = 102 liter (alternative vinkler, AC / BD)
![]() BAC = 78 liter (Co-indvendige vinkler, AB / / CD)
BAC = 78 liter (Co-indvendige vinkler, AB / / CD)
øvelse 4
brug en alternatie sekvens af trin for at finde ![]() BAC.
BAC.
Øvelse 5
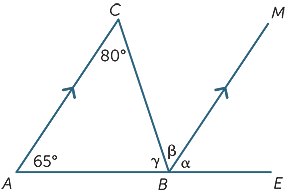 Brug kun Egenskaber for parallelle linjer, find (med grunde) de manglende vinkler i det følgende diagram.
Brug kun Egenskaber for parallelle linjer, find (med grunde) de manglende vinkler i det følgende diagram.
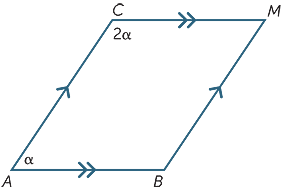
øvelse 6
Find værdien af kur i det følgende diagram.
Converse udsagn
mange udsagn i matematik har en converse, hvor implikationen går i modsat retning. For eksempel slutter udsagnet
‘hvert lige tal i 0, 2, 4, 6 eller 8.’
har samtale
‘hvert tal, der slutter i 0, 2, 4, 6 eller 8, er lige.’
denne særlige erklæring og dens omvendte er begge sande, men dette er på ingen måde altid
tilfældet.
for eksempel er følgende to udsagn samtaler om hinanden:
‘hvert multiplum af 4 er et lige tal.’
‘ hvert lige tal er et multiplum af 4.’
og her er den første sætning sand, men den anden er falsk.
øvelse 7
skriv ned:
a![]() en sand geometrisk erklæring, hvis omvendte også er sandt,
en sand geometrisk erklæring, hvis omvendte også er sandt,
b![]() falsk geometrisk erklæring, hvis omvendte er sandt,
falsk geometrisk erklæring, hvis omvendte er sandt,
c![]() en falsk geometrisk erklæring, hvis omvendte også er falsk.
en falsk geometrisk erklæring, hvis omvendte også er falsk.
de omvendte sætninger for parallelle linjer
vi har set, at tilsvarende vinkler dannet af parallelle linjer er ens. Vi kan skrive ned den omvendte erklæring som følger.
erklæring: hvis linjerne er parallelle, er de tilsvarende vinkler ens.
Converse: Hvis de tilsvarende vinkler er ens, er linjerne parallelle.
den omvendte erklæring er også sand og bruges ofte til at bevise, at to linjer er parallelle. Det samme gælder for alternative og co-indvendige vinkler.
erklæring: hvis linjerne er parallelle, er de alternative vinkler ens.
Converse: hvis de alternative vinkler er ens,så er linjerne parallelle.
erklæring: hvis linjerne er parallelle, er de co-indvendige vinkler supplerende.
Converse: Hvis de co-indvendige vinkler er supplerende, er linjerne parallelle.
i hvert diagram er linjerne AB og CD således parallelle.

øvelse 8
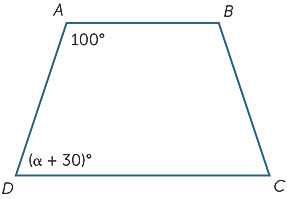 hvilken værdi af karrus vil gøre AB parallel til CD?
hvilken værdi af karrus vil gøre AB parallel til CD?
bevis for de tre samtaler
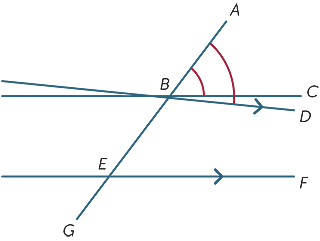 vi antager, at de tilsvarende vinkler dannet af tværgående er lige, og vi viser, at linjerne er parallelle.
vi antager, at de tilsvarende vinkler dannet af tværgående er lige, og vi viser, at linjerne er parallelle.
i diagrammet antager vi, at ![]() ABC =
ABC = ![]() BEF.
BEF.
hvis BC og EF ikke er parallelle, skal du tegne
BD parallelt med EF.
nu da BD og EF er parallelle ![]() ABD =
ABD = ![]() BEF og så
BEF og så ![]() ABC =
ABC = ![]() ABD, hvilket er klart umuligt, medmindre linjerne BC og BD er de samme. Derfor er linjerne BC og EF parallelle.
ABD, hvilket er klart umuligt, medmindre linjerne BC og BD er de samme. Derfor er linjerne BC og EF parallelle.
de andre beviser følger på samme måde.
øvelse 9
Giv et bevis på den anden omvendte sætning (alternative vinkler).
vinkel summen af en trekant
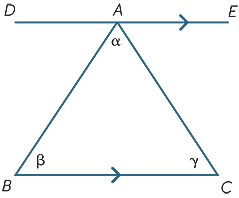 resultaterne fra det foregående afsnit kan bruges til at udlede en af de vigtigste fakta inden for geometri − vinkelsummen af en trekant er 180 liter .
resultaterne fra det foregående afsnit kan bruges til at udlede en af de vigtigste fakta inden for geometri − vinkelsummen af en trekant er 180 liter .
vi begynder med trekant ABC med vinkler L. A., L. A., L. A. Som vist. Tegn linjen DAE parallelt med BC. Derefter,
![]() DAB = venstre (alternative vinkler, BC||de)
DAB = venstre (alternative vinkler, BC||de)
![]() EAC = Kurt (alternative vinkler, BC||de)
EAC = Kurt (alternative vinkler, BC||de)
Kurt+ Kurt + Kurt = 180 Kurt (lige vinkel).
således har vi bevist sætningen
summen af vinklerne i en trekant er 180 liter.
en firkant er en plan figur afgrænset af fire sider.
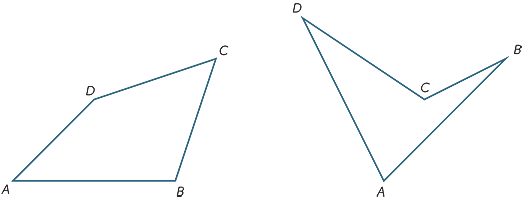
øvelse 10
ved at dividere den firkantede ABCD i to trekanter, find summen af vinklerne.
Links fremad
materialet i dette modul er begyndt at placere geometri på et rimeligt systematisk fundament af omhyggeligt definerede objekter, aksiomer, der skal antages, og sætninger, som vi har bevist. På dette grundlag kan vi udvikle en systematisk redegørelse for plane geometri involverer:
- Pythagoras’ sætning
- kongruens og kongruente trekanter
- lighed og lignende trekanter
- ligebenede og ligesidede trekanter
- specielle firkanter, herunder firkanter, rektangler, parallelogrammer, rhombusser og trapeser
- geometrien af cirkler.
Plane geometri vil også være grundlæggende i mange andre områder af år 7-10 matematik:
- transformationer
- tredimensionel geometri
- områder og volumener
- trigonometri
- koordinatgeometri
- graferne over cirkler og paraboler.
ideerne om tangenter og områder fører igen til beregning i år 11-12.
historie og anvendelse
historie
de utrolige konstruktioner af pyramiderne og de enorme templer i Egypten afslører, at egypterne må have haft en meget god arbejdskendskab og forståelse af grundlæggende geometri, i det mindste på et praktisk niveau. På den anden side er der ingen beviser for, at de havde systematiseret denne viden på nogen formel måde. Dette blev overladt til de gamle grækere. Vi har ikke detaljeret kendskab til denne systematisering, bortset fra påstanden om, at Thales (ca. 624 f. kr. – ca. 546 f. kr.) gav de første’ bevis ‘ for geometriske fakta, der markerede begyndelsen på deduktiv geometri. Pythagoras skole fortsatte dette arbejde, og Platon (428 f.kr. -348 f. kr.) trækker tydeligt på tidligere matematikers arbejde, når han nævner geometriske fakta i sine skrifter. Den geometriske dialog i hans arbejde Meno, hvor Socrates får en slavedreng til at nå frem til en geometrisk sætning ved en række logiske fradrag, er værd at læse. Hvis geometriens oprindelse er uklar, er det’ endelige produkt ‘ ikke. Euclid (323-283 f.kr.), der skrev i Aleksandria, producerede et bemærkelsesværdigt arbejde, kaldet elementerne, som forblev standard lærebog i geometri i mere end 2000 år. I dette arbejde beskriver Euclid en række definitioner (såsom for punkter og linjer), postulater og almindelige forestillinger. (Disse dage kalder vi dem aksiomer.) Fra disse udviklede han logisk i en meget omhyggeligt valgt rækkefølge mange sætninger, som vi generelt omtaler som euklidisk geometri. Der er en række andre geometriske resultater, såsom Pappus’ sætning, der blev opdaget efter Euclid, men disse er generelt ikke dækket i gymnasiet.
et af Euclids fem postulater var ikke så åbenlyst sandt, som de andre syntes at være. En version af det, kendt som Playfairs aksiom, siger, at: Givet en linje  og et punkt P, ikke på
og et punkt P, ikke på  , er der en og kun en linje parallelt med
, er der en og kun en linje parallelt med  passerer gennem P. I det 19. århundrede stillede en række matematikere spørgsmålet ‘Hvad sker der, hvis vi benægter dette postulat? Dette gøres ved at antage, at der enten ikke er en sådan parallel linje, eller ved at sige, at der er mere end en sådan linje. Dette førte til udviklingen af ikke-euklidiske geometrier, hvoraf den ene har vist sig at give en af de gode modeller for universet.
passerer gennem P. I det 19. århundrede stillede en række matematikere spørgsmålet ‘Hvad sker der, hvis vi benægter dette postulat? Dette gøres ved at antage, at der enten ikke er en sådan parallel linje, eller ved at sige, at der er mere end en sådan linje. Dette førte til udviklingen af ikke-euklidiske geometrier, hvoraf den ene har vist sig at give en af de gode modeller for universet.
applikationer
i en meget reel forstand danner geometri og geometrisk intuition grundlaget for alle
matematik − geometri fører til koordinatgeometri, der fører til beregning og
alle dens mange applikationer − og det er også afgørende i læseplanen.
på et mere praktisk niveau har bygherrer, landmålere, ingeniører og arkitekter været tunge brugere af geometri og geometriske ideer i århundreder. For nylig har udviklingen af computere, grafikere og designere tilsluttet sig denne gruppe mennesker, der har brug for og bruger geometri i deres arbejde. På spørgsmålet for nylig, hvor nyttig geometri er, Jim Kelly, sagde en anvendt videnskabsmand: … geometri er en vigtig del af design, tegning og computermodellering. Det bruges også ofte i … fysik og andre fysiske videnskabskurser som en del af forståelsen af virkningerne af belastninger på strukturer og afbalanceringspunkter(tyngdepunkter) for sammensatte faste stoffer. I kemi er forståelse af geometrien af et molekyle relateret til forståelse af stoffernes egenskaber. Der findes mange flere eksempler. (fra Spørg en videnskabsmand hjemmeside.)
en historie om matematik: En introduktion, 3. udgave, Victor J. kats, Addison, (2008)
historie af matematik, D. E. Smith, Dover publikationer, (1958)
svar på øvelser
øvelse 1
ØVELSE 2
De punkter, der er collinear
MOTION 3
60°
ØVELSE 4
![]() DBA = 102° (svarende vinkler, AB||CD)
DBA = 102° (svarende vinkler, AB||CD)
![]() BAC = 78° (co-indvendige vinkler, AC||BD)
BAC = 78° (co-indvendige vinkler, AC||BD)
ØVELSE 5
α = 65°![]() (svarende vinkler, AC||BM)
(svarende vinkler, AC||BM)
β = 80°![]() (alternative vinkler, AC||BM)
(alternative vinkler, AC||BM)
γ + β = 115°![]() (co-indvendige vinkler, AC||BM)
(co-indvendige vinkler, AC||BM)
Derfor, γ = 35°
(Dette er den struktur for et bevis for, at det resultat, at den vinkel summen i en trekant er 180°)
øvelse 6
liter = 60 liter
øvelse 7
a ![]() en firkant med hver af dens indvendige vinkler en ret vinkel er et rektangel.
en firkant med hver af dens indvendige vinkler en ret vinkel er et rektangel.
Converse: hver indvendig vinkel på et rektangel er en ret vinkel.
b![]() et rektangel er en firkant
et rektangel er en firkant
Converse: en firkant er et rektangel
c![]() vinkelsummen af de indvendige vinkler i en trekant er 200 liter
vinkelsummen af de indvendige vinkler i en trekant er 200 liter
Converse: en polygon, for hvilken summen af den indvendige vinkel er 200 liter, er en trekant.
øvelse 8
liter = 50 liter
øvelse 9
vi henviser til det samme diagram.
Placer et punkt H på linjen EF til venstre for E.
![]() CBE =
CBE = ![]() BEH
BEH
hvis BC og EF ikke er parallelle, skal du tegne BD parallelt med EF.
da BD og EF er parallelle, ![]() EBD=
EBD= ![]() BEH, hvilket klart er umuligt, medmindre linjerne BC og BD er de samme.
BEH, hvilket klart er umuligt, medmindre linjerne BC og BD er de samme.
derfor er linjerne BC og EF parallelle.
øvelse 10
360°
det Forbedring af matematikundervisning i skoler (TIMES) projekt 2009-2011 blev finansieret af det australske Regeringsdepartement for Uddannelse, Beskæftigelse og arbejdspladsrelationer.
de synspunkter, der udtrykkes her, er forfatterens og repræsenterer ikke nødvendigvis synspunkterne fra det australske Regeringsdepartement for Uddannelse, Beskæftigelse og arbejdspladsrelationer.
Kristian University of Melbourne på vegne af Det Internationale Center for uddannelse i matematik (ICE-EM), uddannelsesafdelingen for Australian Mathematical Sciences Institute (AMSI), 2010 (medmindre andet er angivet). Dette værk er licenseret under Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()