katamorfismen for begge er en generalisering af dens fold. Katamorfismen muliggør operationer, der ikke er tilgængelige via fold.
denne artikel er en del af en artikelserie om katamorfier. En katamorfisme er en universel abstraktion, der beskriver, hvordan man fordøjer en datastruktur til en potentielt mere kompakt værdi.
denne artikel præsenterer katamorfismen for begge (også kendt som resultat), samt hvordan man identificerer den. Begyndelsen af denne artikel præsenterer katamorfismen i C# med eksempler. Resten af artiklen beskriver, hvordan man kan udlede katamorfismen. Denne del af artiklen præsenterer mit arbejde i Haskell. Læsere, der ikke er fortrolige med Haskell, kan bare læse den første del og overveje resten af artiklen som et valgfrit bilag.
enten er en databeholder, der modellerer to gensidigt eksklusive resultater. Det bruges ofte til at returnere værdier, der kan være enten korrekte (højre) eller forkerte (venstre). I statisk maskinskrevet funktionel programmering med en præference for samlede funktioner, Enten tilbyder en renere, mere fornuftig måde at modellere succes og fejl resultater end at kaste undtagelser.
C# katamorfisme #
denne artikel bruger kirken kodning af enten. Katamorfismen for begge er Match – metoden:
T Match<T>(Func<L, T> onLeft, Func<R, T> onRight);
indtil denne artikel har alle tidligere katamorfier været et par lavet af en indledende værdi og en funktion. Enten katamorfisme er en generalisering, da det er et par funktioner. Den ene funktion håndterer sagen, hvor der er en venstre værdi, og den anden funktion håndterer sagen, hvor der er en rigtig værdi. Begge funktioner skal returnere den samme, samlende type, som ofte er en streng eller noget lignende, der kan vises i en brugergrænseflade:
> IEither<TimeSpan, int> e = new Left<TimeSpan, int>(TimeSpan.FromMinutes(3));> e.Match(ts => ts.ToString(), i => i.ToString())"00:03:00"> IEither<TimeSpan, int> e = new Right<TimeSpan, int>(42);> e.Match(ts => ts.ToString(), i => i.ToString())"42"
du vil ofte se eksempler som ovenstående, der forvandler både venstre og højre sager til strenge eller noget, der kan repræsenteres som en samlende svartype, men dette er på ingen måde påkrævet. Hvis du kan komme med en samlende type, kan du konvertere begge sager til den type:
> IEither<Guid, string> e = new Left<Guid, string>(Guid.NewGuid());> e.Match(g => g.ToString().Count(c => 'a' <= c), s => s.Length)12> IEither<Guid, string> e = new Right<Guid, string>("foo");> e.Match(g => g.ToString().Count(c => 'a' <= c), s => s.Length)3
i de to ovenstående eksempler bruger du to forskellige funktioner, der begge reducerer henholdsvis Guid og string værdier til et tal. Den funktion, der forvandler Guid værdier til et tal, tæller, hvor mange af de seksadecimale cifre, der er større end eller lig med A (10). Den anden funktion returnerer simpelthen længden af string, hvis den er der. Det eksempel giver lidt mening, men Match – metoden er ligeglad med det.
i praktisk brug bruges enten ofte til fejlhåndtering. Artiklen om Kirkens kodning af enten indeholder et eksempel.
enten f-Algebra #
som i den foregående artikel vil jeg bruge Fix og cata som forklaret i Bartos Milevskis fremragende artikel om F-algebraer.
mens F-algebraer og faste punkter for det meste bruges til rekursive datastrukturer, kan du også definere en F-Algebra for en ikke-rekursiv datastruktur. Du så allerede et eksempel på det i artiklerne om boolsk katamorfisme og måske katamorfisme. Forskellen mellem f. eks. måske værdier og enten er, at begge tilfælde af enten bærer en værdi. Du kan modellere dette som en Functor med både en transportørtype og to typeargumenter for de data, der enten kan indeholde:
data EitherF l r c = LeftF l | RightF r deriving (Show, Eq, Read) instance Functor (EitherF l r) where fmap _ (LeftF l) = LeftF l fmap _ (RightF r) = RightF r
jeg valgte at kalde ‘datatyperne’ l (til venstre) og r (til højre) og transportørtypen c (til transportør). Som det også var tilfældet med BoolF og MaybeF, ignorerer instansen Functor kortfunktionen, fordi bæretypen mangler fra både LeftF – sagen og RightF – sagen. Ligesom Functor instanserne for BoolF og MaybeF ser det ud til, at der ikke sker noget, men på typeniveau er dette stadig en oversættelse fra EitherF l r ctil EitherF l r c1. Ikke meget af en funktion, måske, men absolut en endofunctor.
som det også var tilfældet ved at udlede måske og liste katamorfier, er Haskell ikke så glad for at definere forekomster for en type som Fix (EitherF l r). For at løse dette problem kan du introducere en newtype indpakning:
newtype EitherFix l r = EitherFix { unEitherFix :: Fix (EitherF l r) } deriving (Show, Eq, Read)
du kan definere Functor, Applicative, Monad, osv. forekomster til denne type uden at ty til nogen funky GHC-udvidelser. Husk, at i sidste ende er formålet med al denne kode bare at finde ud af, hvordan katamorfismen ser ud. Denne kode er ikke beregnet til faktisk brug.
et par hjælpefunktioner gør det lettere at definere EitherFix værdier:
leftF :: l -> EitherFix l rleftF = EitherFix . Fix . LeftF rightF :: r -> EitherFix l rrightF = EitherFix . Fix . RightF
med disse funktioner kan du oprette EitherFix værdier:
Prelude Data.UUID Data.UUID.V4 Fix Either> leftF <$> nextRandomEitherFix {unEitherFix = Fix (LeftF e65378c2-0d6e-47e0-8bcb-7cc29d185fad)}Prelude Data.UUID Data.UUID.V4 Fix Either> rightF "foo"EitherFix {unEitherFix = Fix (RightF "foo")}
det er alt hvad du behøver for at identificere katamorfismen.
Haskell katamorfisme #
på dette tidspunkt har du to ud af tre elementer i en F-Algebra. Du har en endofunctor (EitherF l r) og et objekt c, men du skal stadig finde en morfisme EitherF l r c -> c. Bemærk, at den algebra, du skal finde, er den funktion, der reducerer functor til dens transportørtype c, ikke ‘datatyperne’ l og r. Det tager lidt tid at vænne sig til, men sådan fungerer katamorfier. Dette betyder dog ikke, at du kommer til at ignorere l og r, som du vil se.
som i de foregående artikler, start med at skrive en funktion, der bliver katamorfismen, baseret på cata:
eitherF = cata alg . unEitherFix where alg (LeftF l) = undefined alg (RightF r) = undefined
mens dette kompilerer, med dets undefined implementeringer, gør det naturligvis ikke noget nyttigt. Jeg finder dog, at det hjælper mig med at tænke. Hvordan kan du returnere en værdi af typen c fra LeftF – sagen? Du kan sende et argument til funktionen eitherF :
eitherF fl = cata alg . unEitherFix where alg (LeftF l) = fl l alg (RightF r) = undefined
mens du teknisk set kunne videregive et argument af typen c til eitherF og derefter returnere denne værdi fra LeftF – sagen, ville det betyde, at du ville ignorere l – værdien. Dette ville være forkert, så i stedet gør argumentet til en funktion og kalder det med l. Ligeledes kan du behandle RightF sagen på samme måde:
eitherF :: (l -> c) -> (r -> c) -> EitherFix l r -> ceitherF fl fr = cata alg . unEitherFix where alg (LeftF l) = fl l alg (RightF r) = fr r
det virker. Da cata har typen Functor f => (f a -> a) -> Fix f -> a, betyder det, at alghar typen f a -> a. I tilfælde af EitherF udleder kompilatoren, at funktionen alg har typen EitherF l r c -> c, hvilket er lige hvad du har brug for!
du kan nu se, hvad bæretypen c er til. Det er den type, som algebra udtrækker, og dermed den type, som katamorfismen vender tilbage.
dette er så katamorfismen for begge. Som hidtil har været konsekvent, er det et par, men nu lavet af to funktioner. Som du har set gentagne gange, er dette ikke den eneste mulige katamorfisme, da du for eksempel trivielt kan vende argumenterne til eitherF.
jeg har valgt repræsentationen vist her, fordi den er isomorf til either funktionen fra Haskells indbyggede Data.Either modul, som kalder funktionen “Case analyse for Either typen”. Begge disse funktioner (eitherF og either) svarer til ovenstående C# Match metode.
Basis #
du kan implementere de fleste andre nyttige funktioner med eitherF. Her er instansen
instance Bifunctor EitherFix where bimap f s = eitherF (leftF . f) (rightF . s)
fra den instans følger Functor instansen trivielt:
instance Functor (EitherFix l) where fmap = second
oven på Functor kan du tilføje Applicative:
instance Applicative (EitherFix l) where pure = rightF f <*> x = eitherF leftF (<$> x) f
Bemærk, at <*> implementeringen svarer til <*> implementeringen for MaybeFix. Det samme er tilfældet for Monad instansen:
instance Monad (EitherFix l) where x >>= f = eitherF leftF f x
ikke kun er EitherFix Foldable, det er Bifoldable:
instance Bifoldable EitherFix where bifoldMap = eitherF
Bemærk interessant, at bifoldMap er identisk med eitherF.
instansen Bifoldable giver dig mulighed for trivielt at implementere instansen Foldable :
instance Foldable (EitherFix l) where foldMap = bifoldMap mempty
du kan finde tilstedeværelsen af mempty forvirrende, da bifoldMap (eller eitherF; de er identiske) tager som argumenter to funktioner. Er mempty en funktion?
Ja, mempty kan være en funktion. Her er det. Der er en Monoid forekomst for enhver funktion a -> m, hvor m er en Monoid forekomst, og mempty er identiteten for den monoid. Det er tilfældet i brug her.
ligesom EitherFix er Bifoldable, det er også Bitraversable:
instance Bitraversable EitherFix where bitraverse fl fr = eitherF (fmap leftF . fl) (fmap rightF . fr)
du kan komfortabelt implementere Traversable instansen baseret på Bitraversable instansen:
instance Traversable (EitherFix l) where sequenceA = bisequenceA . first pure
endelig kan du implementere konverteringer til og fra standard Either – typen ved hjælp af ana som den dobbelte af cata:
toEither :: EitherFix l r -> Either l rtoEither = eitherF Left Right fromEither :: Either a b -> EitherFix a bfromEither = EitherFix . ana coalg where coalg (Left l) = LeftF l coalg (Right r) = RightF r
Dette viser, at EitherFix er isomorf til Either, hvilket igen fastslår, at eitherF og either er ækvivalente.
forhold #
i denne serie har du set forskellige eksempler på katamorfier af strukturer, der ikke har folder, katamorfier, der falder sammen med folder, og nu en katamorfisme, der er mere generel end folden. Introduktionen til serien omfattede dette diagram:
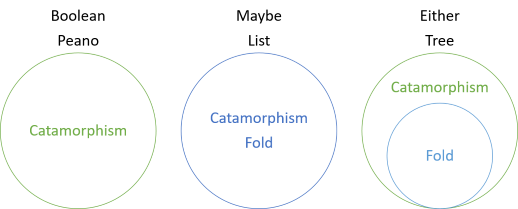
dette viser, at boolske værdier og Peano-tal har katamorfier, men ingen folder, mens for måske og liste er folden og katamorfismen den samme. For begge er folden imidlertid et specielt tilfælde af katamorfisme. Folden for enten ‘foregiver’, at venstre side ikke eksisterer. I stedet fortolkes den venstre værdi som en manglende højre værdi. For at folde begge værdier skal du således angive en’ fallback ‘ – værdi, der vil blive brugt, hvis en af værdierne ikke er en rigtig værdi:
Prelude Fix Either> e = rightF LT :: EitherFix Integer OrderingPrelude Fix Either> foldr (const . show) "" e"LT"Prelude Fix Either> e = leftF 42 :: EitherFix Integer OrderingPrelude Fix Either> foldr (const . show) "" e""
i en GHCi-session som ovenstående kan du oprette to enten værdier af samme type. Den rigtige sag er en Ordering værdi, mens den venstre sag er en Integer værdi.
med foldr er der ingen måde at få adgang til den venstre sag. Mens du kan få adgang til og omdanne den rigtige Ordering værdi, ignoreres tallet 42 simpelthen under folden. I stedet returneres standardværdien "".
kontrast dette med katamorfismen, som kan få adgang til begge tilfælde:
Prelude Fix Either> e = rightF LT :: EitherFix Integer OrderingPrelude Fix Either> eitherF show show e"LT"Prelude Fix Either> e = leftF 42 :: EitherFix Integer OrderingPrelude Fix Either> eitherF show show e"42"
i en session som denne genskaber du de samme værdier, men ved hjælp af katamorfismen eitherF kan du nu få adgang til og omdanne både venstre og højre sager. Med andre ord giver katamorfismen dig mulighed for at udføre operationer, der ikke er mulige med folden.
det er dog interessant at bemærke, at mens folden er en specialisering af katamorfismen, er bifolden identisk med katamorfismen.
Resume #
katamorfismen for begge er et par funktioner. Den ene funktion transformerer den venstre sag, mens den anden funktion transformerer den rigtige sag. For en hvilken som helst værdi vil kun en af disse funktioner blive brugt.
da jeg oprindeligt stødte på begrebet katamorfisme, fandt jeg det vanskeligt at skelne mellem katamorfisme og fold. Mit problem var, tror jeg, at de tutorials, jeg løb ind i, mest brugte linkede lister til at demonstrere, hvordan folden i så fald er katamorfismen. Det viser sig imidlertid, at dette ikke altid er tilfældet. En katamorfisme er en generel abstraktion. En fold synes derimod for det meste at være relateret til samlinger.
i denne artikel så du det første eksempel på en katamorfisme, der kan gøre mere end folden. For begge er folden bare et specielt tilfælde af katamorfisme. Du så dog også, hvordan katamorfismen var identisk med bifolden. Således er det stadig ikke helt klart, hvordan disse begreber forholder sig. Derfor får du i den næste artikel et eksempel på en beholder, hvor der ikke er bifold, og hvor katamorfismen faktisk er en generalisering af folden.
næste: Trækatamorfisme.