modulace délky kanálu v MOSFETu (VLSI Design)

Posted on by admin

terminologie:

  • IDS = proud z odtoku do zdroje nebo odtoku-zdroj proudu
  • VDS = odtok do zdrojového napětí
  • L = délka kanálu

nyní pro ideální případ, v oblasti saturace, se IDS stává nezávislým na VDS, tj. v oblasti saturace je kanál na odtokovém konci sevřen a další zvýšení VDS nemá žádný vliv na tvar kanálu.

ale v praxi zvýšení VDS má vliv na kanál. V oblasti nasycení, když se VDS zvětšuje, je bod sevření kanálu mírně posunut od odtoku směrem ke zdroji, když ho vypouštěcí elektronové pole „tlačí“ zpět. Oblast deplece zpětného zkreslení se rozšiřuje a efektivní délka kanálu se snižuje o množství ∆L pro zvýšení VDS.

kanál se tak již“ nedotýká “ odtoku a získává asymetrický tvar, který je na odtokovém konci tenčí. Tento jev je známý jako modulace délky kanálu.

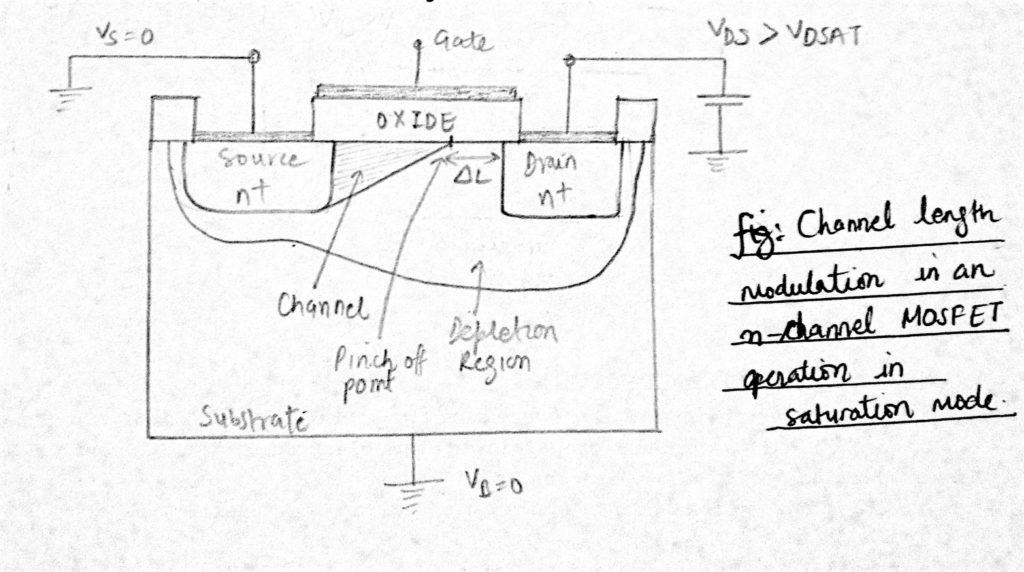
modulace délky kanálu v MOSFETu

modulace délky kanálu tak může být definována jako změna nebo zmenšení délky kanálu (L) v důsledku zvýšení odtoku na zdrojové napětí (VDS) v oblasti nasycení.

u velkých zařízení je tento efekt zanedbatelný, ale u kratších zařízení ∆L/L se stává důležitým. Také v oblasti saturace v důsledku modulace délky kanálu se IDS zvyšuje se zvýšením VDS a také se zvyšuje se snížením délky kanálu L.

křivka napětí a proudu již není v této oblasti plochá.

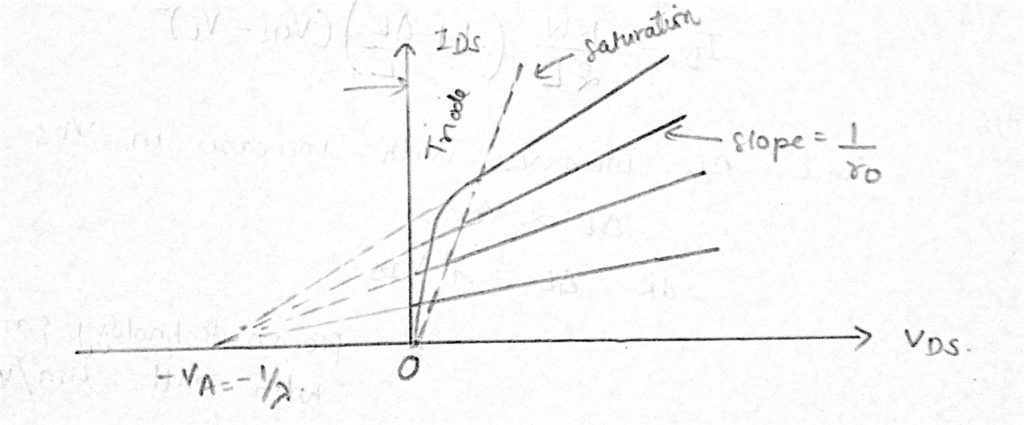
odtokový proud s modulací délky kanálu je dán:

\boxed{I_{DS} = I_{D} = I_{Dsat} (1+ \ lambda V_{DS})}

odvození:

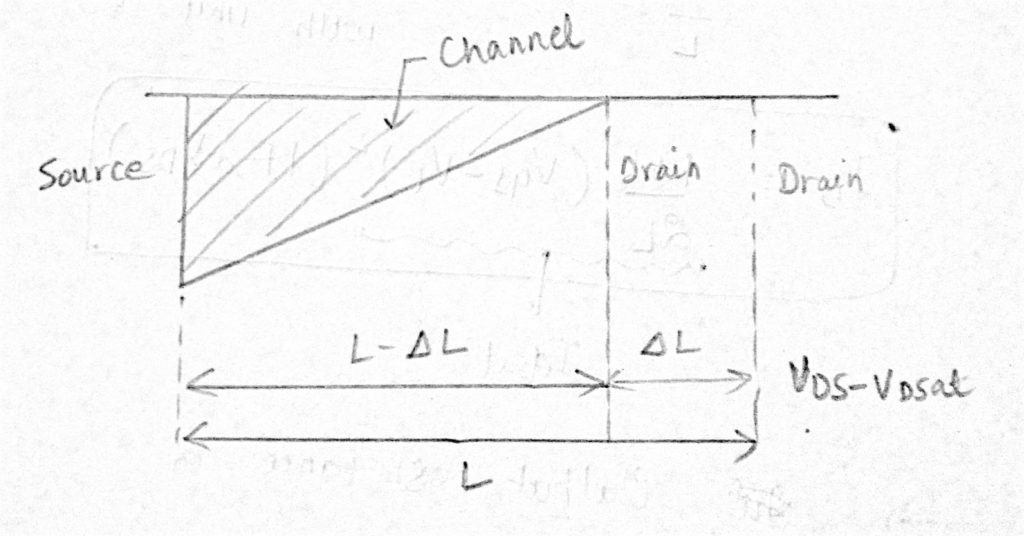
odvození modulace délky kanálu

pro zohlednění závislosti ID na VDS v oblasti saturace nahraďte L L – ∆L. víme, že v oblasti saturace je odtok do zdrojového proudu (IDS = ID) dán:

{I_{D} = \frac{kW}{2L} (v_{GS} - v_{t})^{2}}

{I_{D} = \left (\frac{k}{2} \ right)\left (\frac{W}{L - \ triangle l}\right) (V_{GS} - v_{t})^{2}}

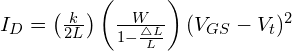
{I_{D} = \left (\frac{k}{2L}\right)\left (\frac{W}{1 - \frac {\triangle L}{L}}\right) (V_{GS} - v_{t})^{2}}

za předpokladu {\frac {\triangle L}{L} 1}

{I_{D} =\left (\frac{kW}{2L}\right)\left ({1+ \ frac {\triangle L}{L}}\right) (V_{GS} - v_{t})^{2}}

vzhledem k tomu, ∆l zvyšuje s nárůstem VDS

{\trojúhelník L\propto V_{DS}}

nebo

{\trojúhelník L= \lambda^ { '} V_{DS}}

kde {\lambda^{ '}} = parametr technologie procesu s jednotkou µm / v.

{ I_{D}=\left (\frac{kW}{2L}\right)\left ({1+ \ frac {\lambda^{ '} V_{DS}}{L}}\right) (V_{GS} - v_{t})^{2}}

proto,

\boxed{I_{DS} = I_{D} = I_{Dsat} (1+ \ lambda V_{DS})}

kde,

{\frac {\lambda^{ ' }} {L} = \lambda} = parametr technologie procesu s jednotkou V-1

{I_{Dsat}=\left (\frac{kW}{2L}\right) (v_{GS} - v_{t})^{2}}

Napsat komentář

Vaše e-mailová adresa nebude zveřejněna.