Toto je krok za krokem průvodce, jak spustit analýzu klastrů k-means v tabulce aplikace Excel od začátku do konce. Vezměte prosím na vědomí, že na tomto webu je k dispozici šablona aplikace Excel, která automaticky spouští analýzu klastrů. Ale pokud chcete vědět, jak spustit shlukování k-znamená v Excelu sami, pak je tento článek pro vás.
kromě tohoto článku mám také video, jak spustit analýzu clusteru v aplikaci Excel.
- první krok-začněte se sadou dat
- krok dva-pokud jen dvě proměnné, použijte scatter graf v Excelu
- krok tři-Vypočítejte vzdálenost od každého datového bodu ke středu clusteru
- jak výpočet funguje?
- Krok čtyři-Vypočítejte průměr (průměr) každé sady klastrů
- krok pět-opakujte krok 3-Vzdálenost od revidovaného průměru
- poslední krok-graf a shrnutí shluků
první krok-začněte se sadou dat
Obrázek 1
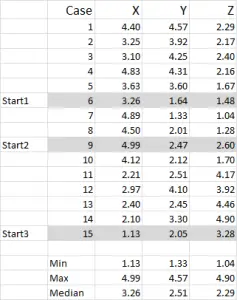
pro tento příklad používám 15 případů (nebo respondentů), kde máme data pro tři proměnné-obecně označené X, Y A Z.
měli byste si všimnout, že data jsou v tomto příkladu škálována 1-5. Vaše data mohou být v jakékoli formě s výjimkou Jmenovité datové stupnice (viz článek o tom, jaké údaje použít).
poznámka: raději používám zmenšená data – ale není to povinné. Důvodem je „obsahovat“ jakékoli odlehlé hodnoty. Řekněme například, že používám údaje o příjmech (demografické měřítko) – většina údajů může být kolem 40 000 až 100 000 USD, ale mám jednu osobu s příjmem 5 000 USD.je pro mě jednodušší klasifikovat tuto osobu do příjmové skupiny „přes 250 000 USD“ a měřítko příjmu 1-9 – ale to je na vás v závislosti na datech, se kterými pracujete.
z této ukázkové sady můžete vidět, že byly zvýrazněny tři počáteční pozice-o těch budeme diskutovat ve třetím kroku níže.
krok dva-pokud jen dvě proměnné, použijte scatter graf v Excelu
Obrázek 2
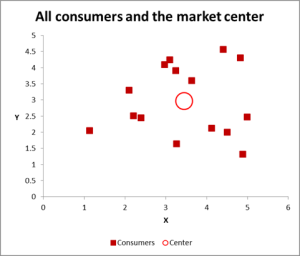
v tomto příkladu analýzy clusteru používáme tři proměnné-ale pokud máte ke shlukování pouze dvě proměnné, pak je scatter graf vynikajícím způsobem, jak začít. A občas můžete data seskupit vizuálními prostředky.
jak můžete vidět v tomto grafu rozptylu, každý jednotlivý případ (pro tento příklad volám spotřebitele) byl mapován spolu s průměrem (průměr) pro všechny případy (červený kruh).
v závislosti na tom, jak zobrazujete data / graf-zdá se, že existuje několik shluků. V tomto případě byste mohli identifikovat tři nebo čtyři relativně odlišné shluky-jak je znázorněno na následujícím grafu.
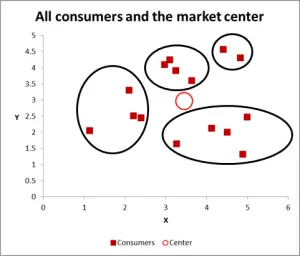
obrázek 3
s tímto dalším grafem, viditelně jsem identifikoval pravděpodobný shluk a kroužil je. Jak jsem navrhl, dobrý přístup, když je třeba zvážit pouze dvě proměnné – ale v tomto případě máme tři proměnné (a můžete mít více), takže tento vizuální přístup bude fungovat pouze pro základní datové sady – takže nyní se podívejme na to, jak provést výpočet Excel pro shlukování k-znamená.
krok tři-Vypočítejte vzdálenost od každého datového bodu ke středu clusteru
pro tento průchozí příklad předpokládejme, že chceme identifikovat pouze tři segmenty/klastry. Ano, Ve výše uvedeném diagramu jsou patrné čtyři shluky, ale to se dívá pouze na dvě proměnné. Vezměte prosím na vědomí, že tento přístup aplikace Excel můžete použít k identifikaci tolika klastrů, kolik chcete-postupujte podle stejného konceptu, jak je vysvětleno níže.
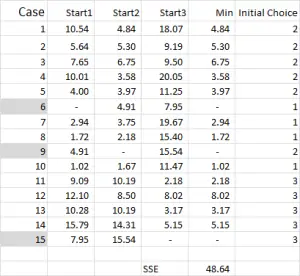
obrázek 4
pro shlukování K-znamená obvykle vyberete některé náhodné případy (výchozí body nebo semena), abyste mohli začít s analýzou.
v tomto příkladu-protože chci vytvořit tři klastry, budu potřebovat tři výchozí body. Pro tyto počáteční body jsem vybral případy 6, 9 a 15 – ale všechny náhodné body by mohly být také vhodné.
důvod, proč jsem vybral tyto případy, je ten, že – při pohledu pouze na proměnnou X-případ 6 byl medián, případ 9 byl maximální a případ 15 byl minimální. To naznačuje, že tyto tři případy se navzájem poněkud liší, takže dobré výchozí body, jak jsou rozloženy.
přečtěte si článek o tom, proč klastrová analýza někdy generuje různé výsledky.
s odkazem na výstup tabulky-toto je náš první výpočet v aplikaci Excel a generuje naši „počáteční volbu“ klastrů. Start 1 jsou data pro případ 6, start 2 je případ 9 a start 3 je případ 15. Měli byste si uvědomit, že průsečík každého z nich dává v tabulce 0 ( -).
jak výpočet funguje?
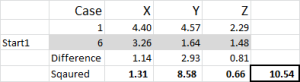
obrázek 5
podívejme se na první číslo v tabulce – případ 1, Začátek 1 = 10,54.
nezapomeňte, že jsme libovolně označili případ 6 jako náš náhodný počáteční bod pro Cluster 1. Chceme vypočítat vzdálenost a použijeme metodu součtu čtverců-jak je znázorněno zde. Vypočítáme rozdíl mezi každým ze tří datových bodů v sadě a poté rozdíly vyrovnáme a pak je sečteme.
můžeme to udělat „mechanicky“, jak je ukázáno zde-ale Excel má vestavěný vzorec pro použití: SUMXMY2 – to je mnohem efektivnější použití.
s odkazem na obrázek 4 pak najdeme minimální vzdálenost pro každý případ od každého ze tří počátečních bodů – to nám říká, ke kterému clusteru (1, 2 nebo 3) je případ nejblíže – což je znázorněno ve sloupci „počáteční volba“.
Krok čtyři-Vypočítejte průměr (průměr) každé sady klastrů
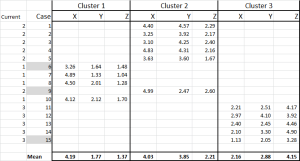
obrázek 6
nyní jsme každý případ přidělili jeho počátečnímu clusteru – a můžeme to rozložit pomocí příkazu IF v tabulce (jak je znázorněno na obrázku 6).
ve spodní části tabulky máme průměr (průměr) každého z těchto případů. N0w – namísto spoléhání se pouze na jeden „reprezentativní“ datový bod – máme sadu případů představujících každý.
krok pět-opakujte krok 3-Vzdálenost od revidovaného průměru
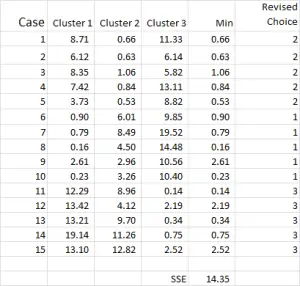
Obrázek 7
proces analýzy clusteru se nyní stává otázkou opakování kroků 4 a 5 (iterací), dokud se clustery stabilizují.
pokaždé použijeme revidovaný průměr pro každý cluster. Proto Obrázek 7 ukazuje naši druhou iteraci – ale tentokrát používáme prostředky generované ve spodní části obrázku 6 (místo počátečních bodů z obrázku 1).
nyní můžete vidět, že došlo k mírné změně v aplikaci clusteru, přičemž případ 9-Jeden z našich výchozích bodů-byl přerozdělen.
můžete také vidět součet kvadratické chyby (SSE) vypočtené dole-což je součet každé z minimálních vzdáleností. Naším cílem je nyní opakovat kroky 4 a 5, dokud SSE nezobrazí pouze minimální zlepšení a / nebo změny alokace clusteru nebudou při každé iteraci malé.
poslední krok-graf a shrnutí shluků
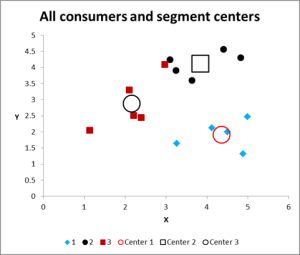
Obrázek 8
po spuštění více iterací máme nyní výstup pro graf a shrnutí dat.
zde je výstupní graf pro tento příklad Excel analýzy clusteru.
jak vidíte, jsou zobrazeny tři odlišné shluky spolu s centroidy (průměr) každého shluku-větší symboly –
v případě potřeby můžeme tato data také prezentovat ve formě tabulky, jak jsme to zpracovali v aplikaci Excel.
podívejte se prosím na případ v clusteru 3-malý červený čtverec hned vedle černé tečky v horní polovině grafu. Tento případ tam sedí kvůli vlivu třetí proměnné, která není zobrazena na tomto grafu dvou proměnných.