předpokládané znalosti
studenti budou mít rozsáhlé neformální zkušenosti s geometrií v dřívějších letech, což poskytne dobrý intuitivní základ pro systematičtější přístup ke geometrii vhodný v letech 7-10. Konkrétní témata z let F-6 relevantní pro tento modul jsou:
- použití kompasů a pravítek a pečlivé kreslení geometrických obrazců.
- typy úhlů, včetně alespoň pravých úhlů, ostrých úhlů, tupých úhlů a
reflexních úhlů. - trojúhelníky, včetně neformálního úvodu do rovnoramenných a rovnostranných trojúhelníků.
- Čtyřúhelníky, včetně neformálního úvodu do čtverců, obdélníků, rovnoběžníků, lichoběžníků a kosočtverců.
- Neformální zkušenosti s překlady, odrazy, rotacemi a zvětšeními,
a se symetrií v kontextu činností, jako je skládání rovnoramenného trojúhelníku, obdélníku nebo kosočtverce.
Motivace
 geometrie se používá k modelování světa kolem nás. Pohled na střechy domů odhaluje trojúhelníky, lichoběžníky a obdélníky, zatímco obklady v chodnících a koupelnách používají šestiúhelníky, pětiúhelníky, trojúhelníky a čtverce.
geometrie se používá k modelování světa kolem nás. Pohled na střechy domů odhaluje trojúhelníky, lichoběžníky a obdélníky, zatímco obklady v chodnících a koupelnách používají šestiúhelníky, pětiúhelníky, trojúhelníky a čtverce.
stavitelé, obkladači, architekti, grafici a webdesignéři běžně používají geometrické nápady ve své práci. Klasifikace takových geometrických objektů a studium jejich vlastností jsou velmi důležité. Geometrie má také mnoho aplikací v umění.
stejně jako aritmetika má čísla jako základní předměty studia, tak body, čáry a kruhy jsou základními stavebními kameny rovinné geometrie.
v geometrii středních škol začínáme řadou intuitivních myšlenek (body, čáry a úhly), které není vůbec snadné přesně definovat, následované některými definicemi (vertikálně protilehlé úhly, rovnoběžky atd.) a z nich odvozujeme důležitá fakta, která jsou často označována jako věty. Na střední škole by se úroveň přísnosti měla vyvíjet pomalu z jednoho roku na druhý, ale v každé fázi je jasné stanovení velmi důležité a mělo by být zdůrazněno.
geometrie tak dává studentům příležitost rozvíjet svou geometrickou intuici, která má uplatnění v mnoha oblastech života, a také se naučit konstruovat logické argumenty a provádět dedukce v prostředí, které je z větší části nezávislé na počtu
.
obsah
body a čáry
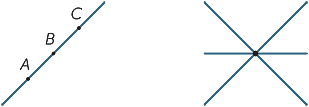
nejjednodušší objekty v rovinné geometrii jsou body a čáry. Protože jsou tak jednoduché, je těžké dát přesné definice z nich, takže místo toho se snažíme dát studentům hrubý popis jejich vlastností, které jsou v souladu s naší intuici. Bod označuje pozici, ale nemá žádnou velikost. V praxi, když nakreslíme bod, má jasně určitou šířku, ale představuje bod v naší představivosti. Čára nemá šířku a nekonečně se rozprostírá v obou směrech. Když nakreslíme čáru, má šířku a má konce, takže to ve skutečnosti není čára, ale představuje čáru v naší představivosti. Vzhledem ke dvěma odlišným bodům A A B pak existuje jedna (a pouze jedna) čára, která prochází oběma body. Používáme velká písmena k označení bodů a řádků názvu buď uvedením dvou bodů na řádku, nebo pomocí malých písmen, jako je  a m. níže uvedený řádek je tedy označován jako řádek AB nebo jako řádek
a m. níže uvedený řádek je tedy označován jako řádek AB nebo jako řádek  .
.

vzhledem ke dvěma odlišným liniím existují dvě možnosti: mohou se buď setkat v jednom bodě, nebo se nikdy nesetkají, bez ohledu na to, jak daleko jsou rozšířeny(nebo vyrobeny). Linky, které se nikdy nesetkají, se nazývají paralelní. Ve druhém diagramu píšeme AB / / CD.
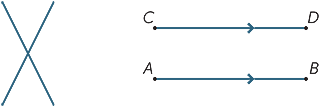
tři (nebo více) bodů, které leží na přímce, se nazývají kolineární.
tři (nebo více) řádků, které se setkávají v jednom bodě, se nazývají souběžné.
|
|
|
| kolineární |
souběžné |
cvičení 1
nakreslete tři čáry, které nejsou souběžné, takže žádné dvě nejsou rovnoběžné.
cvičení 2
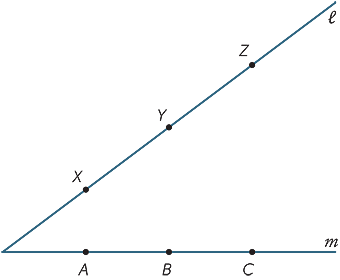
vytvořte velkou kopii níže uvedeného diagramu. Body X, Y, Z jsou libovolné body na řádku  a A ,B, C jsou jakékoli body na řádku m. Připojte se k AY a XB zavolejte jejich průsečík R. Připojte se k BZ a YC a zavolejte jejich průsečík P. Připojte se k CX a ZA a zavolejte jejich průsečík Q. co si všimnete o bodech P, Q, R? (Tento výsledek se nazývá Pappusova věta, c. 340 n. l.)
a A ,B, C jsou jakékoli body na řádku m. Připojte se k AY a XB zavolejte jejich průsečík R. Připojte se k BZ a YC a zavolejte jejich průsečík P. Připojte se k CX a ZA a zavolejte jejich průsečík Q. co si všimnete o bodech P, Q, R? (Tento výsledek se nazývá Pappusova věta, c. 340 n. l.)
intervaly, paprsky a úhly
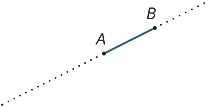 Předpokládejme, že A A B jsou dva body na přímce. Interval
Předpokládejme, že A A B jsou dva body na přímce. Interval
AB je část čáry mezi A A B, včetně dvou koncových bodů.
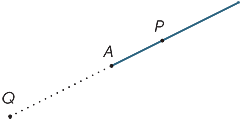 bod a v diagramu rozděluje čáru na dva kusy zvané paprsky. Paprsek AP je paprsek, který obsahuje bod P (a bod A).
bod a v diagramu rozděluje čáru na dva kusy zvané paprsky. Paprsek AP je paprsek, který obsahuje bod P (a bod A).
Úhly
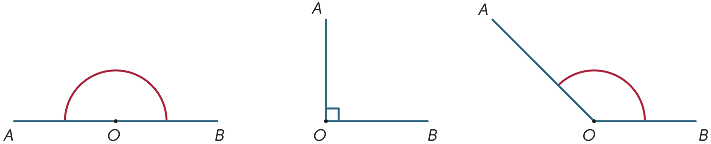
 v diagramu se stínovaná oblast mezi paprsky OA a OB nazývá úhel AOB nebo úhel BOA. Znaménko úhlu
v diagramu se stínovaná oblast mezi paprsky OA a OB nazývá úhel AOB nebo úhel BOA. Znaménko úhlu ![]() je zapsáno, takže píšeme
je zapsáno, takže píšeme ![]() AOB.
AOB.
 stínovaná oblast venku se nazývá reflexní úhel tvořený OA a OB. Většinu času, pokud neurčíme slovo reflex, všechny naše úhly odkazují na oblast mezi paprsky a ne mimo ně.
stínovaná oblast venku se nazývá reflexní úhel tvořený OA a OB. Většinu času, pokud neurčíme slovo reflex, všechny naše úhly odkazují na oblast mezi paprsky a ne mimo ně.
velikost úhlu
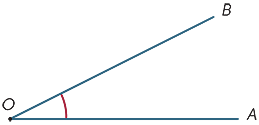 Představte si, že paprsek OB se otáčí kolem bodu O, dokud neleží podél OA. Velikost otáčení se nazývá velikost úhlu AOB. Můžeme podobně definovat velikost reflexního úhlu.
Představte si, že paprsek OB se otáčí kolem bodu O, dokud neleží podél OA. Velikost otáčení se nazývá velikost úhlu AOB. Můžeme podobně definovat velikost reflexního úhlu.
často budeme používat malá řecká písmena, α, β, γ, … reprezentovat velikost úhlu.
velikost úhlu odpovídající jedné úplné revoluci byla rozdělena (Babyloňany) na 360 stejných částí, které nazýváme stupně. (Pravděpodobně si vybrali 360, protože se blížil počtu dní v roce.) Proto je velikost přímého úhlu 180° a velikost pravého úhlu 90°. Další úhly lze měřit (přibližně) pomocí úhloměru.
|
|
||
| přímý úhel | pravý úhel |
tupý úhel |
úhly jsou klasifikovány podle jejich velikosti. Říkáme, že úhel s velikostí α je ostrý
(slovo znamená „ostrý“), pokud 0° < α < 90°, α je tupý (slovo znamená „tupý“), pokud
90° < α < 180° a α je reflexní, pokud 180° < α < 360°.
vzhledem k tomu, že úhloměr má dvě stupnice, musí být studenti opatrní při kreslení a
měření úhlů. Je užitečné použít úhloměr k nakreslení některých úhlů, jako například 30°, 78°, 130°, 163°.
Cvičení 3
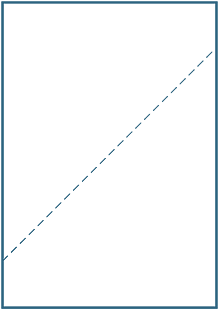 Přeložte list papíru A4 odpovídající (diagonálně) protilehlým rohům. Nakreslete čáru podél vytvořeného záhybu a změřte úhly mezi záhybem a stranou.
Přeložte list papíru A4 odpovídající (diagonálně) protilehlým rohům. Nakreslete čáru podél vytvořeného záhybu a změřte úhly mezi záhybem a stranou.
ve výše uvedeném cvičení tvoří dva úhly dohromady přímku, a tak se přidávají na 180°. Dva úhly, které přidávají na 180°, se nazývají doplňkové úhly; 45° a 135° jsou tedy doplňkové úhly.
dva úhly, které se přidávají k 90°, se nazývají komplementární; 23° a 67° jsou tedy
komplementární úhly.
úhly v bodě
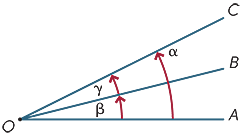 o dvou úhlech v bodě se říká, že sousedí, pokud sdílejí společný paprsek. Proto v diagramu sousedí
o dvou úhlech v bodě se říká, že sousedí, pokud sdílejí společný paprsek. Proto v diagramu sousedí ![]() AOB a
AOB a ![]() BOC.
BOC.
lze přidat sousední úhly, takže v diagramu
α = β + γ.
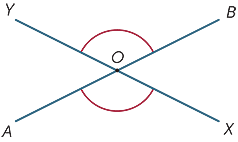
když se protínají dvě čáry, vytvoří se v průsečíku čtyři úhly.
v diagramu se úhly označené ![]() AOX a
AOX a ![]() BOY nazývají vertikálně opačné.
BOY nazývají vertikálně opačné.
 vzhledem k tomu,
vzhledem k tomu,
-
 AOX je doplněk
AOX je doplněk  BOX (přímý úhel).
BOX (přímý úhel). -
 chlapec je také doplněk
chlapec je také doplněk  krabice (přímý úhel),
krabice (přímý úhel),
můžeme konstatovat, že tyto vertikálně opačné úhly, ![]() AOX a
AOX a ![]() BOY jsou stejné. Máme tedy naše první
BOY jsou stejné. Máme tedy naše první
důležité geometrické prohlášení:
vertikálně protilehlé úhly jsou stejné.
výsledek v geometrii (a v matematice obecně) se často nazývá věta. Věta je důležitým tvrzením, které lze prokázat logickou dedukcí. Výše uvedený argument je důkazem věty; někdy jsou důkazy předloženy formálně po prohlášení věty.
 pokud se protínají dvě čáry tak, že všechny čtyři úhly jsou pravoúhlé, pak se říká, že čáry jsou kolmé.
pokud se protínají dvě čáry tak, že všechny čtyři úhly jsou pravoúhlé, pak se říká, že čáry jsou kolmé.
úhly v bodě-geometrické argumenty
v geometrických argumentech lze použít následující důvody:
- sousední úhly lze přidat nebo odečíst.
- úhly při otáčkách se přidávají na 360°.
- úhly v přímce se přidávají na 180°.
- svisle protilehlé úhly jsou stejné.
příčné a rovnoběžné čáry
 příčný je čára, která splňuje další dvě čáry.
příčný je čára, která splňuje další dvě čáry.
odpovídající úhly
různé úhly jsou tvořeny příčným. V níže uvedených schématech se dva označené úhly nazývají odpovídající úhly.
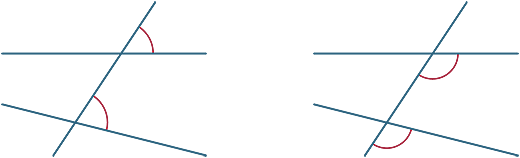
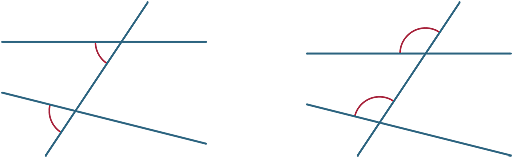
 nyní se podíváme na to, co se stane, když jsou dvě čáry řezané příčným průřezem rovnoběžné.
nyní se podíváme na to, co se stane, když jsou dvě čáry řezané příčným průřezem rovnoběžné.
Inituitivně, pokud by úhel α byl větší než β, CD by překročilo AB nalevo od F a pokud by bylo menší než β, zkřížilo by se napravo od F. takže protože čáry vůbec nekříží, α nemůže být ani menší, ani větší než β a tak se rovná β.
alternativně si představte překládání úhlu QGD podél GF, dokud se G neshoduje s F. protože čáry jsou rovnoběžné, očekávali bychom, že úhel α se bude shodovat s úhlem β. Toto pozorování nás vede k domněnce, že:
odpovídající úhly vytvořené z rovnoběžných čar jsou stejné.
tento výsledek nemůžeme dokázat, i když jsme ukázali, že je geometricky věrohodný. Přijmeme to jako axiom geometrie. Axiom je tvrzení, které nemůžeme dokázat, ale které je intuitivně rozumné. Všimněte si, že mnoho skutečností, které jsme již uvedli, například: mohou být přidány sousední úhly, a dva body určují čáru atd., jsou také axiomy, i když jsme je tímto způsobem výslovně neuvedli.
alternativní úhly
v každém diagramu se dva označené úhly nazývají alternativní úhly (protože jsou na střídavých stranách příčné).

 pokud jsou čáry AB a CD rovnoběžné, pak jsou alternativní úhly stejné. Tento výsledek lze nyní prokázat.
pokud jsou čáry AB a CD rovnoběžné, pak jsou alternativní úhly stejné. Tento výsledek lze nyní prokázat.
![]() DGQ = α (odpovídající úhly, AB / / CD)
DGQ = α (odpovídající úhly, AB / / CD)
![]() DGQ = β (svisle protilehlé úhly v G)
DGQ = β (svisle protilehlé úhly v G)
takže α = β.
abych to shrnul:
střídavé úhly vytvořené z rovnoběžek jsou stejné.
Co – vnitřní úhly
konečně, v každém diagramu níže, dva označené úhly se nazývají co – vnitřní úhly a leží na stejné straně příčné.

pokud jsou čáry AB a CD rovnoběžné, pak je zřejmé, že společné vnitřní úhly nejsou stejné, ale ukazuje se, že jsou doplňkové, to znamená, že jejich součet je 180° .
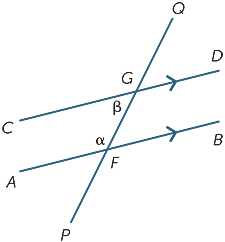 toto je výsledek, který lze také snadno prokázat:
toto je výsledek, který lze také snadno prokázat:
![]() BFG = β (alternativní úhly, AB ||CD)
BFG = β (alternativní úhly, AB ||CD)
α + β = 180° (přímý úhel na F)
abych to shrnul:
společné vnitřní úhly vytvořené z rovnoběžek jsou doplňkové.
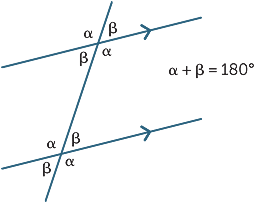 tři výsledky lze shrnout
tři výsledky lze shrnout
následujícím schématem:
numerické příklady
vzhledem k informacím o úhlech v diagramu můžeme výše uvedené výsledky použít k nalezení velikosti dalších úhlů v diagramu. Jedná se o jednoduchou, ale velmi důležitou dovednost, často označovanou neformálně jako pronásledování úhlu. Při řešení problémů není sled kroků vždy jedinečný. Může existovat několik různých, ale stejně platných přístupů.
například v následujícím diagramu hledáme velikost úhlu BAC.

![]() DCA = 102° (střídavé úhly, AC / BD)
DCA = 102° (střídavé úhly, AC / BD)
![]() BAC = 78° (společné vnitřní úhly, AB / / CD)
BAC = 78° (společné vnitřní úhly, AB / / CD)
cvičení 4
použijte alternativní posloupnost kroků k nalezení ![]() BAC.
BAC.
Cvičení 5
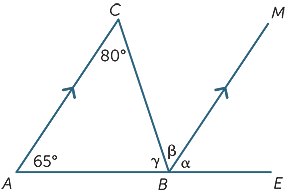 pomocí pouze vlastností rovnoběžných čar Najděte (s důvody) chybějící úhly v následujícím diagramu.
pomocí pouze vlastností rovnoběžných čar Najděte (s důvody) chybějící úhly v následujícím diagramu.
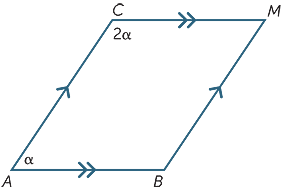
cvičení 6
najděte hodnotu α v následujícím diagramu.
Converse příkazy
mnoho výroků v matematice má converse, ve kterém implikace jde opačným směrem. Například příkaz
‚každé sudé číslo končí 0, 2, 4, 6 nebo 8.‘
má converse
‚každé číslo, které končí 0, 2, 4, 6 nebo 8, je sudé.‘
toto konkrétní tvrzení a jeho konverzace jsou pravdivé, ale v žádném případě to není vždy
případ.
například následující dva příkazy jsou vzájemné konverzace:
‚ každý násobek 4 je sudé číslo.‘
‚ každé sudé číslo je násobkem 4.‘
a zde je první tvrzení pravdivé, ale druhé je nepravdivé.
cvičení 7
zapsat:
a![]() pravdivý geometrický výrok, jehož converse je také pravdivý,
pravdivý geometrický výrok, jehož converse je také pravdivý,
b![]() falešný geometrický výrok, jehož converse je pravdivý,
falešný geometrický výrok, jehož converse je pravdivý,
c![]() falešný geometrický výrok, jehož converse je také nepravdivý.
falešný geometrický výrok, jehož converse je také nepravdivý.
Converse věty pro rovnoběžky
viděli jsme, že odpovídající úhly vytvořené z rovnoběžek jsou stejné. Prohlášení converse můžeme zapsat následovně.
prohlášení: pokud jsou čáry rovnoběžné, pak jsou odpovídající úhly stejné.
Converse: Pokud jsou odpovídající úhly stejné, jsou čáry rovnoběžné.
příkaz converse je také pravdivý a často se používá k prokázání, že dva řádky jsou rovnoběžné. Totéž platí pro alternativní a společné vnitřní úhly.
prohlášení: pokud jsou čáry rovnoběžné, pak jsou alternativní úhly stejné.
Converse: pokud jsou alternativní úhly stejné, pak jsou čáry rovnoběžné.
prohlášení: pokud jsou přímky rovnoběžné, pak jsou společné vnitřní úhly doplňkové.
Converse: Pokud jsou společné vnitřní úhly doplňkové, pak jsou čáry rovnoběžné.
v každém diagramu jsou tedy čáry AB a CD rovnoběžné.

cvičení 8
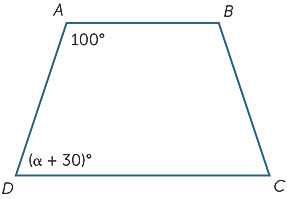 která hodnota α bude AB rovnoběžná s CD?
která hodnota α bude AB rovnoběžná s CD?
důkazy tří konverzí
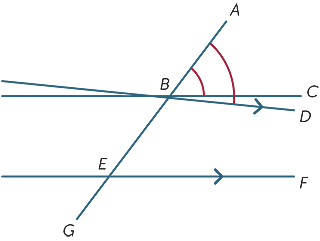 předpokládáme, že odpovídající úhly tvořené příčným průřezem jsou stejné a ukazujeme, že čáry jsou rovnoběžné.
předpokládáme, že odpovídající úhly tvořené příčným průřezem jsou stejné a ukazujeme, že čáry jsou rovnoběžné.
v diagramu předpokládáme, že ![]() ABC =
ABC = ![]() BEF.
BEF.
pokud BC a EF nejsou rovnoběžné, nakreslete
BD rovnoběžně s EF.
nyní, protože BD a EF jsou rovnoběžné ![]() ABD =
ABD = ![]() BEF a tak
BEF a tak ![]() ABC =
ABC = ![]() ABD, což je zjevně nemožné, pokud řádky BC a BD nejsou stejné. Proto jsou linie BC a EF rovnoběžné.
ABD, což je zjevně nemožné, pokud řádky BC a BD nejsou stejné. Proto jsou linie BC a EF rovnoběžné.
ostatní důkazy následují stejným způsobem.
cvičení 9
uveďte důkaz druhé věty converse (alternativní úhly).
úhlový součet trojúhelníku
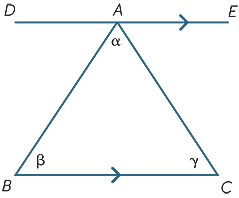 výsledky z předchozí části lze použít k odvození jedné z nejdůležitějších skutečností v geometrii-úhlový součet trojúhelníku je 180° .
výsledky z předchozí části lze použít k odvození jedné z nejdůležitějších skutečností v geometrii-úhlový součet trojúhelníku je 180° .
začínáme trojúhelníkem ABC s úhly α, β, γ, jak je znázorněno. Nakreslete čáru DAE rovnoběžně s BC. Pak,
![]() DAB = β (alternativní úhly, BC / / DE)
DAB = β (alternativní úhly, BC / / DE)
![]() EAC = γ (alternativní úhly, BC||DE)
EAC = γ (alternativní úhly, BC||DE)
α+ β + γ = 180° (přímý úhel).
tak jsme prokázali větu
součet úhlů v trojúhelníku je 180°.
čtyřúhelník je rovinná postava ohraničená čtyřmi stranami.
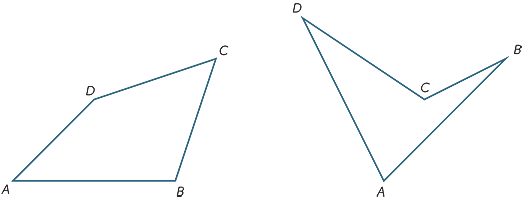
cvičení 10
rozdělením čtyřúhelníku ABCD na dva trojúhelníky Najděte součet úhlů.
odkazy vpřed
materiál v tomto modulu začal umisťovat geometrii na přiměřeně systematický základ pečlivě definovaných objektů, axiomů, které je třeba předpokládat, a vět, které jsme prokázali. Na tomto základě můžeme vytvořit systematický popis rovinné geometrie zahrnující:
- Pythagorova věta
- kongruence a shodné trojúhelníky
- podobnost a podobné trojúhelníky
- rovnoramenné a rovnostranné trojúhelníky
- speciální čtyřúhelníky, včetně čtverců, obdélníků, rovnoběžníků, kosočtverců a lichoběžníků
- geometrie kruhů.
geometrie roviny bude také zásadní v mnoha dalších oblastech matematiky let 7-10:
- transformace
- trojrozměrná geometrie
- plochy a objemy
- trigonometrie
- souřadnicová geometrie
- grafy kruhů a parabol.
myšlenky tečen a oblastí vedou zase k počtu v letech 11-12.
historie a aplikace
historie
neuvěřitelné stavby pyramid a obrovských chrámů Egypta ukazují, že Egypťané museli mít velmi dobré pracovní znalosti a porozumění základní geometrii, alespoň na praktické úrovni. Na druhé straně neexistují žádné důkazy o tom, že by tyto znalosti systematizovali jakýmkoli formálním způsobem. To bylo ponecháno starým Řekům. Nemáme podrobné znalosti o této systematizaci, s výjimkou tvrzení, že Thales (ca. 624 př. n. l. 546
jeden z euclidových pěti postulátů nebyl tak zjevně pravdivý, jak se zdálo, že ostatní jsou. Jedna jeho verze, známý jako Playfairův Axiom uvádí, že: Vzhledem k přímce  a bodu P, nikoli na
a bodu P, nikoli na  , existuje jedna a pouze jedna přímka rovnoběžná s
, existuje jedna a pouze jedna přímka rovnoběžná s  procházející P. v 19. století se řada matematiků ptala na otázku “ co se stane, když tento postulát popřeme?“To se provádí za předpokladu, že buď neexistuje žádná taková rovnoběžka, nebo tím, že existuje více než jedna taková přímka. To vedlo k vývoji neeuklidovských geometrií, z nichž jedna se ukázala jako jeden z dobrých modelů pro vesmír.
procházející P. v 19. století se řada matematiků ptala na otázku “ co se stane, když tento postulát popřeme?“To se provádí za předpokladu, že buď neexistuje žádná taková rovnoběžka, nebo tím, že existuje více než jedna taková přímka. To vedlo k vývoji neeuklidovských geometrií, z nichž jedna se ukázala jako jeden z dobrých modelů pro vesmír.
aplikace
ve velmi reálném smyslu tvoří geometrie a geometrická intuice základy všech
matematiky − geometrie vede ke souřadnicové geometrii, která vede k počtu a
všem jeho mnoha aplikacím-a proto je v učebních osnovách zásadní.
na praktičtější úrovni jsou stavitelé, geodeti, inženýři a architekti po staletí těžkými uživateli geometrie a geometrických myšlenek. V poslední době se s vývojem počítačů připojili grafici a weboví designéři k této skupině lidí, kteří ve své práci potřebují a používají geometrii. Nedávno na otázku, jak užitečná je geometrie, Jim Kelly, řekl aplikovaný vědec: … geometrie je důležitou součástí návrhu, kreslení a počítačového modelování. Používá se také často … kurzy fyziky a dalších fyzikálních věd jako součást pochopení účinků zatížení na struktury a vyvažovacích bodů (těžišť) kompozitních těles. V chemii je pochopení geometrie molekuly spojeno s pochopením vlastností látek. Existuje mnoho dalších příkladů. (z webu Ask a Scientist.)
Dějiny matematiky: Úvod, 3. vydání, Victor J. Katz, Addison-Wesley, (2008)
historie matematiky, D. E. Smith, Dover publikace New York, (1958)
odpovědi na cvičení
cvičení 1
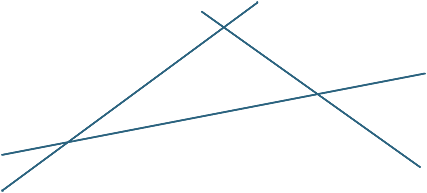
cvičení 2
body jsou kolineární
cvičení 3
60°
cvičení 4
![]() DBA = 102° (odpovídající úhly, AB / / CD)
DBA = 102° (odpovídající úhly, AB / / CD)
![]() BAC = 78° (společné vnitřní úhly, AC||BD)
BAC = 78° (společné vnitřní úhly, AC||BD)
cvičení 5
α = 65°![]() (odpovídající úhly, AC||BM)
(odpovídající úhly, AC||BM)
β = 80°![]() (alternativní úhly, AC||BM)
(alternativní úhly, AC||BM)
γ + β = 115°![]() (společné vnitřní úhly, AC||BM)
(společné vnitřní úhly, AC||BM)
= 35°
(Toto je struktura pro důkaz výsledku, že úhlový součet trojúhelníku je 180°)
cvičení 6
α = 60°
cvičení 7
a![]() čtyřúhelník s každým z jeho vnitřních úhlů pravý úhel je obdélník.
čtyřúhelník s každým z jeho vnitřních úhlů pravý úhel je obdélník.
Converse: každý vnitřní úhel obdélníku je pravý úhel.
b![]() obdélník je čtverec
obdélník je čtverec
Converse: čtverec je obdélník
c![]() úhlový součet vnitřních úhlů trojúhelníku je 200°
úhlový součet vnitřních úhlů trojúhelníku je 200°
Converse: mnohoúhelník, pro který je součet vnitřního úhlu 200°, je trojúhelník.
cvičení 8
α = 50°
cvičení 9
odkazujeme na stejný diagram.
umístěte bod H na přímku EF nalevo od E.
![]() CBE =
CBE = ![]() BEH
BEH
pokud BC a EF nejsou rovnoběžné, nakreslete BD rovnoběžně s EF.
protože BD a EF jsou rovnoběžné, ![]() EBD=
EBD= ![]() BEH, což je zjevně nemožné, pokud řádky BC a BD nejsou stejné.
BEH, což je zjevně nemožné, pokud řádky BC a BD nejsou stejné.
proto jsou linie BC a EF rovnoběžné.
cvičení 10
360°
Projekt zlepšování matematického vzdělávání ve školách (TIMES) 2009-2011 byl financován australským vládním Ministerstvem školství, zaměstnanosti a vztahů na pracovišti.
zde vyjádřené názory jsou názory autora a nemusí nutně představovat názory australského vládního Ministerstva školství, zaměstnanosti a vztahů na pracovišti.
© University of Melbourne jménem Mezinárodního centra excelence pro vzdělávání v matematice (ICE-EM), vzdělávací divize australského Institutu matematických věd (AMSI), 2010 (není-li uvedeno jinak). Tato práce je licencována pod licencí Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()