Assessment | Biopsychology / Comparative |Cognitive | Developmental | Language / Individual differences / Personality | Philosophy |Social /
Methods / Statistics / Clinical | Educational | Industrial / Professional items / World psychology /
Statistics: Scientific method * Research methods * Experimental design * pregradual statistics courses * Statistical tests * Game theory * Decision theory
prosím, pomozte zlepšit tuto stránku sami, pokud je to možné..
Clusterová analýza nebo shlukování je běžná technika pro statistickou analýzu dat, která se používá v mnoha oblastech, včetně strojového učení, dolování dat, rozpoznávání vzorů, analýzy obrazu a bioinformatiky. Shlukování je klasifikace podobných objektů do různých skupin, nebo přesněji rozdělení datové sady na podmnožiny (klastry), takže data v každé podmnožině (ideálně) sdílejí nějakou společnou vlastnost – často blízkost podle nějaké definované míry vzdálenosti.
kromě termínu shlukování dat (nebo jen shlukování) existuje řada termínů s podobným významem, včetně shlukové analýzy, automatické klasifikace,numerické taxonomie, botryologie a typologické analýzy.
- typy shlukování
- hierarchické shlukování
- měření vzdálenosti
- vytváření clusterů
- Aglomerativní hierarchické shlukování
- Partiční shlukování
- k-means a deriváty
- k-means shlukování
- Qt Clust algoritmus
- fuzzy C-znamená shlukování
- kritérium loktů
- spektrální shlukování
- aplikace
- biologie
- marketingový výzkum
- další aplikace
- srovnání mezi shlukováním dat
- Viz také
- bibliografie
- softwarové implementace
- zdarma
typy shlukování
algoritmy shlukování dat mohou být hierarchické nebo částečné. Hierarchické algoritmy nacházejí po sobě jdoucí klastry pomocí dříve vytvořených klastrů, zatímco partiční algoritmy určují všechny klastry najednou. Hierarchické algoritmy mohou být aglomerativní (zdola nahoru) nebo dělící (shora dolů). Aglomerativní algoritmy začínají s každým prvkem jako samostatný cluster a slučují je do postupně větších shluků. Rozdělující algoritmy začínají celou sadou a pokračují v rozdělení na postupně menší klastry.
hierarchické shlukování
měření vzdálenosti
klíčovým krokem v hierarchickém shlukování je výběr míry vzdálenosti. Jednoduchým měřítkem je vzdálenost Manhattanu, která se rovná součtu absolutních vzdáleností pro každou proměnnou. Název pochází ze skutečnosti, že v případě dvou proměnných mohou být proměnné vykresleny na mřížce, kterou lze porovnat s ulicemi města, a vzdálenost mezi dvěma body je počet bloků, které by člověk chodil.
běžnějším měřítkem je euklidovská vzdálenost, vypočtená nalezením čtverce vzdálenosti mezi každou proměnnou, součtem čtverců a nalezením druhé odmocniny této sumy. V případě dvou proměnných je vzdálenost analogická k nalezení délky přepony v trojúhelníku; to znamená, že je to Vzdálenost “ jak vrána letí.“Přehled shlukové analýzy ve výzkumu psychologie zdraví zjistil, že nejběžnějším měřítkem vzdálenosti v publikovaných studiích v této oblasti výzkumu je euklidovská vzdálenost nebo čtvercová euklidovská vzdálenost.
vytváření clusterů
vzhledem k měření vzdálenosti lze prvky kombinovat. Hierarchické shlukování staví (aglomerativní), nebo rozpadá (dělitelný), hierarchie shluků. Tradiční reprezentace této hierarchie je stromová datová struktura (nazývaná dendrogram), s jednotlivými prvky na jednom konci a jediným clusterem s každým prvkem na druhém. Aglomerativní algoritmy začínají v horní části stromu, zatímco dělicí algoritmy začínají dole. (Na obrázku šipky označují aglomerativní shlukování.)
řezání stromu v dané výšce poskytne shlukování s vybranou přesností. V následujícím příkladu řezání za druhým řádkem přinese shluky {a} {b c} {d e} {f}. Řezání po třetí řadě přinese shluky {a} {b c} {d e f}, což je hrubší shlukování, s menším počtem větších shluků.
Aglomerativní hierarchické shlukování
Předpokládejme například, že tato data mají být seskupena. Kde euklidovská vzdálenost je metrika vzdálenosti.
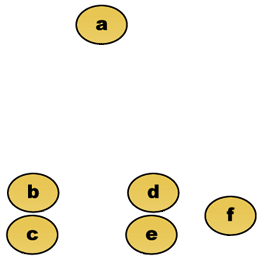
nezpracovaná data
hierarchický shlukovací dendrogram by byl jako takový:
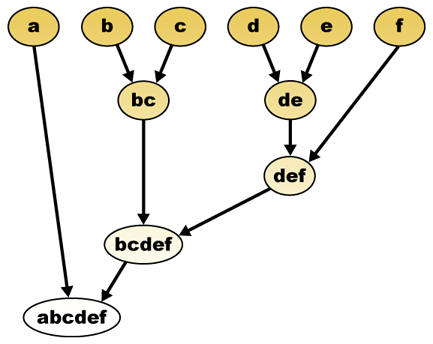
tradiční reprezentace
tato metoda vytváří hierarchii z jednotlivých prvků postupným slučováním klastrů. Opět máme šest prvků {a} {b} {c} {d} {e} A {f}. Prvním krokem je určení, které prvky se mají sloučit do clusteru. Obvykle chceme vzít dva nejbližší prvky, proto musíme definovat vzdálenost 
Předpokládejme, že jsme sloučili dva nejbližší prvky b A c, nyní máme následující klastry {a}, {b, C}, {d}, {e} A {f} a chceme je dále sloučit. Ale k tomu musíme vzít vzdálenost mezi {A} a {b C}, a proto definovat vzdálenost mezi dvěma shluky. Obvykle je vzdálenost mezi dvěma klastry 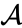
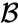
- maximální vzdálenost mezi prvky každého clusteru (nazývané také úplné shlukování vazeb):
- minimální vzdálenost mezi prvky každého clusteru (také nazývaná shlukování jednotlivých vazeb):
- střední vzdálenost mezi prvky každého clusteru (také nazývané průměrné shlukování vazeb):
- součet všech rozptylů uvnitř klastru
- zvýšení rozptylu pro sloučený klastr (Wardovo kritérium)
- pravděpodobnost, že kandidátské klastry vzniknou ze stejné distribuční funkce (v-vazba)
každá aglomerace se vyskytuje ve větší vzdálenosti mezi shluky než předchozí aglomerace, a člověk se může rozhodnout zastavit shlukování buď když shluky jsou příliš daleko od sebe, aby mohly být sloučeny (kritérium vzdálenosti) nebo pokud existuje dostatečně malý počet klastrů(kritérium počtu).
Partiční shlukování
k-means a deriváty
k-means shlukování
algoritmus k-means přiřadí každý bod clusteru, jehož střed (nazývaný také centroid)je nejbližší. Střed je průměr všech bodů v klastru — to znamená, že jeho souřadnice jsou aritmetickým průměrem pro každou dimenzi zvlášť nad všemi body v klastru.
příklad: Datová sada má tři rozměry a cluster má dva body: X = (x1, x2, x3) a Y = (y1, y2, y3). Pak se centroid Z stává Z = (z1, z2, z3), kde z1 = (x1 + y1)/2 a z2 = (x2 + y2)/2 a z3 = (x3 + y3)/2.
algoritmus je zhruba (J. MacQueen, 1967):
- náhodně generujte klastry k a určete centra klastrů nebo přímo generujte body semen k jako centra klastrů.
- přiřaďte každý bod nejbližšímu centru clusteru.
- přepočítat nová centra clusteru.
- opakujte, dokud není splněno nějaké konvergenční kritérium (obvykle se přiřazení nezměnilo).
hlavními výhodami tohoto algoritmu jsou jeho jednoduchost a rychlost, která mu umožňuje běžet na velkých datových sadách. Jeho nevýhodou je, že při každém běhu nepřináší stejný výsledek, protože výsledné klastry závisí na počátečních náhodných přiřazeních. Maximalizuje rozptyl mezi klastry (nebo minimalizuje rozptyl uvnitř klastru), ale nezajišťuje, aby výsledek měl globální minimum rozptylu.
Qt Clust algoritmus
Qt (Quality Threshold) shlukování (Heyer et al, 1999) je alternativní metoda dělení dat, vynalezená pro shlukování genů. To vyžaduje větší výpočetní výkon než k-prostředky, ale nevyžaduje zadání počtu clusterů a priori, a vždy vrátí stejný výsledek při spuštění několikrát.
algoritmus je:
- uživatel zvolí maximální průměr klastrů.
- Vytvořte kandidátský cluster pro každý bod zahrnutím nejbližšího bodu, dalšího nejbližšího atd., Dokud průměr clusteru nepřekročí práh.
- Uložte klastr kandidátů s největším počtem bodů jako první skutečný klastr a odstraňte všechny body v klastru z dalšího zvážení.
- Recurse se sníženou sadou bodů.
vzdálenost mezi bodem a skupinou bodů se vypočítá pomocí úplné vazby, tj. jako maximální vzdálenost od bodu ke každému členu skupiny (viz část „Aglomerativní hierarchické shlukování“ o vzdálenosti mezi shluky).
fuzzy C-znamená shlukování
ve fuzzy shlukování má každý bod určitý stupeň příslušnosti ke shlukům, jako ve fuzzy logice, spíše než zcela patřit pouze k jednomu shluku. Tím pádem, body na okraji clusteru, může být v clusteru v menší míře než body ve středu clusteru. Pro každý bod x máme koeficient udávající stupeň bytí v klastru kth 

s fuzzy C-prostředky, těžiště clusteru je průměr všech bodů, vážený jejich stupněm příslušnosti ke clusteru:
stupeň sounáležitosti souvisí s inverzní vzdáleností ke clusteru
pak jsou koeficienty normalizovány a fuzzyfied s reálným parametrem 
pro m rovno 2 to odpovídá normalizaci koeficientu lineárně, aby se jejich součet 1. Když je m Blízko 1, pak centrum clusteru nejblíže k bodu má mnohem větší váhu než ostatní a algoritmus je podobný k-prostředkům.
algoritmus fuzzy C-means je velmi podobný algoritmu k-means:
- vyberte několik klastrů.
- přiřaďte náhodně každému bodovému koeficientu za to, že je v klastrech.
- opakujte, dokud algoritmus konverguje (to znamená, že změna koeficientů mezi dvěma iteracemi není větší než
, daný práh citlivosti) :
- Vypočítejte těžiště pro každý cluster pomocí výše uvedeného vzorce.
- pro každý bod Vypočítejte jeho koeficienty v klastrech pomocí výše uvedeného vzorce.
algoritmus minimalizuje rozptyl uvnitř clusteru, ale má stejné problémy jako k-prostředky, minimum je lokální minimum a výsledky závisí na počáteční volbě závaží.
kritérium loktů
kritérium loktů je běžným pravidlem pro určení, jaký počet shluků by měl být zvolen, například pro K-prostředky a aglomerativní hierarchické shlukování.
kritérium lokte říká, že byste měli zvolit počet klastrů, aby přidání dalšího klastru nepřidalo dostatečné informace. Přesněji, pokud grafujete procento rozptylu vysvětlené shluky proti počtu shluků, první shluky přidají mnoho informací (vysvětlují hodně rozptylu), ale v určitém okamžiku mezní zisk klesne, což dává úhel v grafu (loket).
na následujícím grafu je loket označen červeným kruhem. Počet vybraných shluků by proto měl být 4.
spektrální shlukování
vzhledem k množině datových bodů může být matice podobnosti definována jako matice {\displaystyle s} kde 

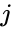
jednou z takových technik je algoritmus Shi-Malik, běžně používaný pro segmentaci obrazu. Rozděluje body do dvou množin 

z {\displaystyle s}, kde 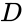
toto rozdělení může být provedeno různými způsoby, například tím, že se vezme medián 



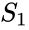
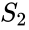
příbuzný algoritmus je algoritmus Meila-Shi, který vezme vlastní vektory odpovídající k největším vlastním číslům matice 
aplikace
biologie
v biologii clustering má mnoho aplikací v oblasti výpočetní biologie a bioinformatiky, z nichž dvě jsou:
- v transkriptomice se shlukování používá k vytváření skupin genů se souvisejícími expresními vzory. Tyto skupiny často obsahují funkčně příbuzné proteiny, jako jsou enzymy pro specifickou cestu nebo geny, které jsou koregulovány. Vysoce výkonné experimenty s použitím exprimovaných sekvenčních značek (est) nebo DNA microarrays mohou být výkonným nástrojem pro anotaci genomu, obecný aspekt genomiky.
- v sekvenční analýze se shlukování používá ke skupině homologních sekvencí do genových rodin. Jedná se o velmi důležitý koncept v bioinformatice a evoluční biologii obecně. Viz evoluce duplikací genů.
marketingový výzkum
klastrová analýza je široce používána v průzkumu trhu při práci s vícerozměrnými daty z průzkumů a testovacích panelů. Výzkumníci trhu používají klastrovou analýzu k rozdělení obecné populace spotřebitelů na segmenty trhu a k lepšímu pochopení vztahů mezi různými skupinami spotřebitelů/potenciálních zákazníků.
- segmentace trhu a určení cílových trhů
- polohování produktu
- vývoj nových produktů
- výběr testovacích trhů (viz : experimentální techniky)
další aplikace
analýza sociálních sítí: při studiu sociálních sítí lze shlukování použít k rozpoznání komunit ve velkých skupinách lidí.
segmentace obrazu: shlukování lze použít k rozdělení digitálního obrazu na odlišné oblasti pro detekci hranic nebo rozpoznávání objektů.
dolování dat: mnoho aplikací pro dolování dat zahrnuje rozdělení datových položek do souvisejících podmnožin; marketingové aplikace diskutované výše představují některé příklady. Další běžnou aplikací je rozdělení dokumentů, jako jsou webové stránky World Wide, do žánrů.
srovnání mezi shlukováním dat
existuje několik návrhů na míru podobnosti mezi dvěma shlukováním. Takové opatření lze použít k porovnání toho, jak dobře fungují různé algoritmy shlukování dat na sadě dat. Mnoho z těchto opatření je odvozeno z matrice shody (aka confusion matrix), např. Rand opatření a Fowlkes-Mallows BK opatření.
- Jain, Murty and Flynn: Data Clustering: a Review, ACM Comp. Surve., 1999. K dispozici zde.
- pro další prezentaci hierarchických, k-prostředků a fuzzy c-prostředků viz tento úvod do shlukování. Také má vysvětlení o směsi Gaussians.
- David Dowe, stránka modelování směsí-další odkazy na shlukování a modely směsí.
- výukový program o shlukování
- on-line učebnice: teorie informací, Inference a učení algoritmy, David J. C. MacKay obsahuje kapitoly o K-znamená shlukování, měkké K-znamená shlukování a derivace včetně e-m algoritmu a variační pohled na e-m algoritmu.
Viz také
- k-means
- umělá neuronová síť (ANN)
- Samoorganizující se mapa
- maximalizace očekávání (EM)
bibliografie
- Clatworthy, J., Buick, D., Hankins, m., Weinman, J., & Horne, R. (2005). Použití a vykazování klastrové analýzy v psychologii zdraví: přehled. British Journal of Health Psychology 10: 329-358.
- Romesburg, h. Clarles, Cluster Analysis for Researchers, 2004, 340 stran. ISBN 1411606175 nebo nakladatelství, dotisk 1990 vydání vydané Krieger Pub. Spolupráce… Japonský překlad je k dispozici od Uchida Rokakuho Publishing Co., Ltd., Tokio, Japonsko.
- Heyer, LJ, Kruglyak, s. and Yooseph, s., zkoumání expresních dat: identifikace a analýza Koexpresovaných genů, výzkum genomu 9: 1106-1115.
- on-line učebnice: teorie informace, Inference, a učení algoritmy, David J. C. MacKay obsahuje kapitoly o K-znamená shlukování, měkké K-znamená shlukování, a derivace včetně e-m algoritmu a variační pohled na e-m algoritmu.
pro spektrální shlukování :
- Jianbo Shi and Jitendra Malik, „Normalized Cuts and Image Segmentation“, IEEE Transactions on Pattern Analysis and Machine Intelligence, 22(8), 888-905, August 2000. K dispozici na domovské stránce Jitendra Malik
- Marina Meila a Jianbo Shi, „segmentace učení s náhodnou chůzí“, Neural Information Processing Systems, NIPS, 2001. K dispozici na domovské stránce Jianbo Shi
pro odhad počtu klastrů:
- Can, F., Ozkarahan, E. a. (1990) “ koncepty a účinnost metodiky shlukování založené na koeficientu krytí pro textové databáze.“Transakce ACM v databázových systémech. 15 (4) 483-517.
softwarové implementace
zdarma
- balíček flexclust pro R
- YALE (Yet Another Learning Environment): bezplatný open-source software pro zjišťování znalostí a dolování dat včetně pluginu pro shlukování
- některé zdrojové soubory MATLABu pro shlukování zde
- COMPACT – Comparative Package for Clustering Assessment (také v Matlabu)
- mixmod : Klastr Založený Na Modelu A Diskriminační Analýza. Kód v C++, rozhraní s Matlab a Scilab
- LingPipe Clustering Tutorial Tutorial pro to kompletní-a single-link clustering pomocí LingPipe, Java text dolování dat balíček distribuován se zdrojem.
- Weka: Weka obsahuje nástroje pro předběžné zpracování dat, klasifikaci, regresi, shlukování, asociační pravidla a vizualizaci. Je také vhodný pro vývoj nových schémat strojového učení.