Katamorfismus pro oba je zobecněním jeho záhybu. Katamorfismus umožňuje operace, které nejsou dostupné přes fold.
tento článek je součástí série článků o katamorfismech. Katamorfismus je univerzální abstrakce, která popisuje, jak strávit datovou strukturu do potenciálně kompaktnější hodnoty.
tento článek představuje katamorfismus pro buď (také známý jako výsledek), a jak jej identifikovat. Začátek tohoto článku představuje katamorfismus v C#, s příklady. Zbytek článku popisuje, jak odvodit katamorfismus. Tato část článku představuje mou práci v Haskellu. Čtenáři, kteří nejsou spokojeni s Haskellem, si mohou přečíst první část a zbytek článku považovat za volitelný Dodatek.
buď je datový kontejner, který modeluje dva vzájemně se vylučující výsledky. Často se používá k vrácení hodnot, které mohou být buď správné (vpravo), nebo nesprávné (vlevo). Ve staticky typovaném funkcionálním programování s preferencí pro celkové funkce nabízí buď rozumnější a rozumnější způsob, jak modelovat úspěch a výsledky chyb, než házet výjimky.
C # catamorphism #
tento článek používá církevní kódování buď. Katamorfismus pro oba je metoda Match :
T Match<T>(Func<L, T> onLeft, Func<R, T> onRight);
až do tohoto článku byly všechny předchozí katamorfismy dvojicí vytvořenou z počáteční hodnoty a funkce. Katamorfismus je zobecnění, protože se jedná o dvojici funkcí. Jedna funkce zpracovává případ, kdy je levá hodnota, a druhá funkce zpracovává případ, kdy je správná hodnota. Obě funkce musí vrátit stejný, sjednocující Typ, což je často řetězec nebo něco podobného, které lze zobrazit v uživatelském rozhraní:
> IEither<TimeSpan, int> e = new Left<TimeSpan, int>(TimeSpan.FromMinutes(3));> e.Match(ts => ts.ToString(), i => i.ToString())"00:03:00"> IEither<TimeSpan, int> e = new Right<TimeSpan, int>(42);> e.Match(ts => ts.ToString(), i => i.ToString())"42"
často uvidíte příklady, jako je výše uvedené, které mění levý i pravý případ na řetězce nebo něco, co lze reprezentovat jako sjednocující typ odpovědi, ale to není v žádném případě nutné. Pokud můžete přijít s sjednocujícím typem, můžete převést oba případy na tento typ:
> IEither<Guid, string> e = new Left<Guid, string>(Guid.NewGuid());> e.Match(g => g.ToString().Count(c => 'a' <= c), s => s.Length)12> IEither<Guid, string> e = new Right<Guid, string>("foo");> e.Match(g => g.ToString().Count(c => 'a' <= c), s => s.Length)3
ve dvou výše uvedených příkladech používáte dvě různé funkce, které snižují hodnoty Guid a string na číslo. Funkce, která změní hodnoty Guid na číslo, počítá, kolik hexadecimálních číslic je větší nebo rovno A (10). Druhá funkce jednoduše vrátí délku string, pokud je tam. Tento příklad dává malý smysl, ale metoda Match se o to nestará.
v praktickém použití se buď často používá pro zpracování chyb. Článek o církevním kódování obou obsahuje příklad.
buď F-Algebra #
stejně jako v předchozím článku použiji Fix a cata, jak je vysvětleno v vynikajícím článku Bartosze Milewského o f-Algebrách.
zatímco F-algebry a pevné body se většinou používají pro rekurzivní datové struktury, můžete také definovat F-algebru pro nerekurzivní datovou strukturu. Příklad toho jste již viděli v článcích o Booleovském katamorfismu a možná katamorfismu. Možná hodnoty a buď je, že oba případy buď nesou hodnotu. Můžete to modelovat jako Functor jak s typem nosiče, tak se dvěma argumenty typu pro data, která mohou obsahovat:
data EitherF l r c = LeftF l | RightF r deriving (Show, Eq, Read) instance Functor (EitherF l r) where fmap _ (LeftF l) = LeftF l fmap _ (RightF r) = RightF r
rozhodl jsem se zavolat „datové typy“ l (vlevo) a r (vpravo) a typ nosiče c (pro dopravce). Stejně jako tomu bylo v případě BoolF a MaybeF, instance Functor ignoruje funkci mapy, protože typ nosiče chybí jak v případě LeftF, tak v případě RightF. Stejně jako Functor instance pro BoolF a MaybeF se zdá, že se nic neděje, ale na úrovni typu je to stále překlad z EitherF l r c na EitherF l r c1. Ne moc funkce, možná, ale určitě endofunktor.
stejně jako tomu bylo i v případě odvození Katamorfismů možná a seznam, Haskell není příliš šťastný z definování instancí pro typ jako Fix (EitherF l r). Chcete-li tento problém vyřešit, můžete zavést newtype obal:
newtype EitherFix l r = EitherFix { unEitherFix :: Fix (EitherF l r) } deriving (Show, Eq, Read)
můžete definovat Functor, Applicative, Monad, atd. instance pro tento typ, aniž by se uchylovat k jakékoliv funky GHC rozšíření. Mějte na paměti, že nakonec, účelem celého tohoto kódu je jen zjistit, jak vypadá katamorfismus. Tento kód není určen pro skutečné použití.
dvojice pomocných funkcí usnadňuje definování hodnot EitherFix :
leftF :: l -> EitherFix l rleftF = EitherFix . Fix . LeftF rightF :: r -> EitherFix l rrightF = EitherFix . Fix . RightF
pomocí těchto funkcí můžete vytvořit hodnoty EitherFix :
Prelude Data.UUID Data.UUID.V4 Fix Either> leftF <$> nextRandomEitherFix {unEitherFix = Fix (LeftF e65378c2-0d6e-47e0-8bcb-7cc29d185fad)}Prelude Data.UUID Data.UUID.V4 Fix Either> rightF "foo"EitherFix {unEitherFix = Fix (RightF "foo")}
to je vše, co potřebujete k identifikaci katamorfismu.
Haskell catamorfism #
v tomto bodě máte dva ze tří prvků F-algebry. Máte endofunctor (EitherF l r) a objekt c, ale stále musíte najít morfismus EitherF l r c -> c. Všimněte si, že algebra, kterou musíte najít, je funkce, která redukuje funktor na typ nosiče c, nikoli „datové typy“ l a r. To trvá nějaký čas, než si zvyknete, ale tak fungují katamorfismy. To však neznamená, že budete ignorovat l a r, jak uvidíte.
stejně jako v předchozích článcích začněte psaním funkce, která se stane katamorfismem založeným na cata:
eitherF = cata alg . unEitherFix where alg (LeftF l) = undefined alg (RightF r) = undefined
i když se to kompiluje, s implementacemi undefined to zjevně nedělá nic užitečného. Zjistil jsem však, že mi to pomáhá přemýšlet. Jak můžete vrátit hodnotu typu c z případu LeftF? Můžete předat argument funkci eitherF :
eitherF fl = cata alg . unEitherFix where alg (LeftF l) = fl l alg (RightF r) = undefined
i když byste technicky mohli předat argument typu c na eitherF a pak vrátit tuto hodnotu z případu LeftF, znamenalo by to, že byste ignorovali hodnotu l. To by bylo nesprávné, takže místo toho udělejte z argumentu funkci a zavolejte ji pomocí l. Stejně tak se můžete vypořádat s případem RightF stejným způsobem:
eitherF :: (l -> c) -> (r -> c) -> EitherFix l r -> ceitherF fl fr = cata alg . unEitherFix where alg (LeftF l) = fl l alg (RightF r) = fr r
tohle funguje. Protože cata má typ Functor f => (f a -> a) -> Fix f -> a, znamená to, že alg má typ f a -> a. V případě EitherF kompilátor vyvozuje, že funkce alg má typ EitherF l r c -> c, což je přesně to, co potřebujete!
nyní můžete vidět, k čemu je typ nosiče c určen. Je to typ, který algebra extrahuje, a tedy typ, který katamorfismus vrací.
Toto je tedy katamorfismus pro oba. Jak bylo dosud konzistentní, je to pár, ale nyní je vyroben ze dvou funkcí. Jak jste opakovaně viděli, toto není jediný možný katamorfismus, protože můžete například triviálně převrátit argumenty na eitherF.
vybral jsem zde zobrazenou reprezentaci, protože je izomorfní na funkci either z vestavěného modulu Haskell Data.Either, který volá funkci “ Analýza případů pro typ Either„. Obě tyto funkce (eitherF a either) jsou ekvivalentní výše uvedené metodě C# Match.
Basis #
většinu dalších užitečných funkcí můžete implementovat pomocí eitherF. Zde je instance Bifunctor :
instance Bifunctor EitherFix where bimap f s = eitherF (leftF . f) (rightF . s)
z této instance následuje instance Functor triviálně:
instance Functor (EitherFix l) where fmap = second
na vrcholu Functor můžete přidat Applicative:
instance Applicative (EitherFix l) where pure = rightF f <*> x = eitherF leftF (<$> x) f
Všimněte si, že implementace <*> je podobná implementaci <*> pro MaybeFix. Totéž platí pro instanci Monad :
instance Monad (EitherFix l) where x >>= f = eitherF leftF f x
nejen, že je EitherFix Foldable, je to Bifoldable:
instance Bifoldable EitherFix where bifoldMap = eitherF
je zajímavé, že bifoldMap je totožný s eitherF.
instance Bifoldable umožňuje triviálně implementovat instanci Foldable :
instance Foldable (EitherFix l) where foldMap = bifoldMap mempty
možná zjistíte, že přítomnost mempty je záhadná, protože bifoldMap (nebo eitherF; jsou identické) bere jako argumenty dvě funkce. Je mempty funkce?
Ano, mempty může být funkce. Tady to je. Existuje instance Monoid pro libovolnou funkci a -> m, kde m je instance Monoid a mempty je identita pro tento monoid. To je příklad, který se zde používá.
stejně jako EitherFix je Bifoldable, je to také Bitraversable:
instance Bitraversable EitherFix where bitraverse fl fr = eitherF (fmap leftF . fl) (fmap rightF . fr)
instanci Traversable můžete pohodlně implementovat na základě instance Bitraversable :
instance Traversable (EitherFix l) where sequenceA = bisequenceA . first pure
nakonec můžete implementovat konverze do a ze standardního typu Either pomocí ana jako duálního cata:
toEither :: EitherFix l r -> Either l rtoEither = eitherF Left Right fromEither :: Either a b -> EitherFix a bfromEither = EitherFix . ana coalg where coalg (Left l) = LeftF l coalg (Right r) = RightF r
to ukazuje, že EitherFix je izomorfní na Either, což opět dokazuje, že eitherF a either jsou ekvivalentní.
vztahy #
v této sérii jste viděli různé příklady katamorfismů struktur, které nemají záhyby, katamorfismy, které se shodují se záhyby, a nyní katamorfismus, který je obecnější než záhyb. Úvod do série zahrnoval tento diagram:
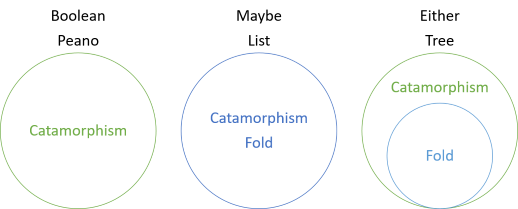
to ukazuje, že booleovské hodnoty a Peanova čísla mají katamorfismy, ale žádné záhyby, zatímco pro Možná a seznam je záhyb a katamorfismus stejný. Pro oba je však záhyb zvláštním případem katamorfismu. Záhyb pro buď „předstírá“, že levá strana neexistuje. Místo toho je levá hodnota interpretována jako chybějící pravá hodnota. Chcete-li tedy složit obě hodnoty, musíte zadat hodnotu „fallback“, která bude použita v případě, že hodnota buď není správnou hodnotou:
Prelude Fix Either> e = rightF LT :: EitherFix Integer OrderingPrelude Fix Either> foldr (const . show) "" e"LT"Prelude Fix Either> e = leftF 42 :: EitherFix Integer OrderingPrelude Fix Either> foldr (const . show) "" e""
v relaci GHCi, jako je výše, můžete vytvořit dvě hodnoty stejného typu. Pravý případ je hodnota Ordering, zatímco levý případ je hodnota Integer.
s foldr neexistuje žádný způsob přístupu k levému pouzdru. Zatímco můžete přistupovat a transformovat správnou hodnotu Ordering, číslo 42 je během skládání jednoduše ignorováno. Místo toho se vrátí výchozí hodnota "".
to kontrastuje s katamorfismem, který může přistupovat k oběma případům:
Prelude Fix Either> e = rightF LT :: EitherFix Integer OrderingPrelude Fix Either> eitherF show show e"LT"Prelude Fix Either> e = leftF 42 :: EitherFix Integer OrderingPrelude Fix Either> eitherF show show e"42"
v takové relaci znovu vytvoříte stejné hodnoty, ale pomocí katamorfismu eitherF můžete nyní přistupovat a transformovat jak levý, tak pravý případ. Jinými slovy, katamorfismus umožňuje provádět operace, které nejsou možné se záhybem.
je však zajímavé poznamenat, že zatímco záhyb je specializací katamorfismu, bifold je totožný s katamorfismem.
shrnutí #
katamorfismus pro buď je dvojice funkcí. Jedna funkce transformuje levý případ, zatímco druhá funkce transformuje správný případ. Pro libovolnou hodnotu bude použita pouze jedna z těchto funkcí.
když jsem se původně setkal s konceptem katamorfismu, zjistil jsem, že je obtížné rozlišovat mezi katamorfismem a složením. Můj problém byl, myslím, že tutoriály, na které jsem narazil, většinou používaly propojené seznamy, aby ukázaly, jak je v tomto případě záhyb katamorfismus. Ukazuje se však, že tomu tak není vždy. Katamorfismus je obecná abstrakce. Na druhou stranu se mi zdá, že záhyb souvisí hlavně se sbírkami.
v tomto článku jste viděli první příklad katamorfismu, který dokáže více než záhyb. Pro oba je záhyb jen zvláštním případem katamorfismu. Také jste však viděli, jak byl katamorfismus totožný s bifoldem. Stále tedy není zcela jasné, jak se tyto pojmy vztahují. Proto v dalším článku získáte příklad kontejneru, kde není bifold a kde katamorfismus je skutečně zobecněním záhybu.
další: stromový katamorfismus.