dnes bude stručný úvod do kruhové statistiky (někdy označované jako směrová statistika). Kruhová statistika je zajímavé rozdělení statistik zahrnující pozorování pořízená jako vektory kolem jednotkového kruhu. Jako příklad si představte měření doby narození v nemocnici během 24hodinového cyklu nebo směrové rozptýlení skupiny stěhovavých zvířat. Tento typ dat je zapojen do různých oblastí, jako je ekologie, klimatologie a biochemie. Povaha měření pozorování kolem jednotkového kruhu vyžaduje odlišný přístup k testování hypotéz. Distribuce musí být „zabaleny“ kolem kruhu, aby byly užitečné, a konvenční odhady, jako je průměr vzorku nebo rozptyl vzorku, neobsahují vodu.
v tomto příspěvku provedeme test rozteče Rao, abychom vyhodnotili uniformitu kruhového datového souboru. Jedná se o základní postup a měl by být považován za úvod do zpracování kruhových dat.
Začínáme
chystáme se provést test hypotézy na Želvách, malý datový soubor sestávající z úhlů příchodu 10 zelených mořských želv na jejich hnízdní ostrov. Naším cílem je zjistit, kde úhly příjezdu vykazují známky směrovosti nebo více svědčí o náhodném rozptylu.
Nejprve nainstalujte balíček circular a připojte datovou sadu želv.
install.packages("circular")require(circular)attach(turtles)
vykreslování dat
balíček circular obsahuje vlastní funkci Vykreslování, plot.circular. Pozorujme příletové úhly želv.
plot.circular(arrival)
zde je děj: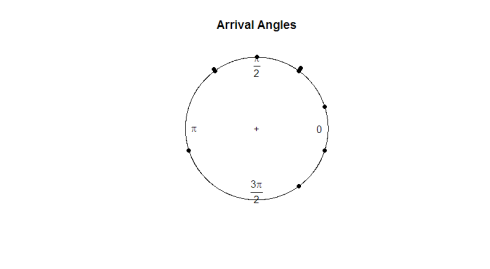
vzhledem k očnímu testu se zdá, že pozorování jsou kolem kruhu jednotná. Pokud chceme spustit test hypotéz, abychom zjistili, zda jsou data skutečně jednotná, budeme muset vyvinout statistiku testů, která pracuje s úhlovými daty.
jaký je pro nás dobrý parametr? Když vezmeme průměr vzorku, moc nám neřekne o směru dat (180 stupňů není užitečným průměrem 2 stupňů a 358 stupňů). Na následujícím grafu pozorujte, jak je průměr vzorku k ničemu při reprezentaci tvaru nebo šíření našich dat.
mean(arrival)plot.circular(mean(arrival)) 0.9120794
zde je děj: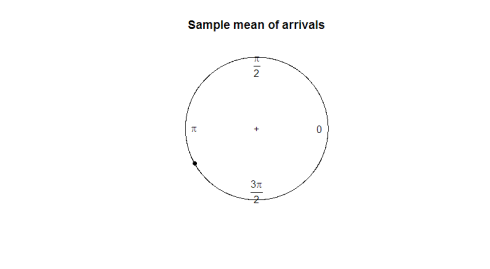
místo toho použijeme metodu, která určuje směrovost měřením průměrného prostoru mezi pozorováními. Tento test se nazývá Raoův Rozestupový Test.
Rao ‚s distance Test
Rao‘ s distance Test byl vyvinut pro posouzení jednotnosti kruhových dat. Využívá prostor mezi pozorováními k určení, zda data vykazují významnou směrovost. Pokud jsou údaje jednotné, pozorování by měla mít tendenci být rovnoměrně od sebe.
zde je statistika testu \(U\) PRO Test rozteče Rao: $$U = 1/2 \ sum\limits_{i=1}^n / t_{i} – λ| $$ kde \(λ = 360 / n, T_{i} = f_{i + 1} – f_{i}\) a \(T_{n} = (360-f_{n})+f_{1}\)
statistika testu v zásadě agreguje odchylky mezi po sobě jdoucími body, každý z nich vážený celkovým počtem pozorování v datovém souboru.
použijeme funkci rao.spacing.test() ke spuštění tohoto testu hypotéz. Naše nulová hypotéza říká, že data mají rovnoměrné rozdělení, zatímco alternativní stavy data vykazují známky směrovosti. Projdeme ten test.
rao.spacing.test(arrival,alpha=.10) Rao's Spacing Test of Uniformity Test Statistic = 127.2689 Level 0.1 critical value = 161.23 Do not reject null hypothesis of uniformity
při statistice testu 127, která spadá pod kritickou hodnotu 161, se data významně neopírají v žádném směru. Nemůžeme odmítnout hypotézu, že příchozí želvy mají rovnoměrné rozložení.
závěr
test rozestupu Rao určil, že data nevykazují žádné známky směrových trendů. Nemůžeme odmítnout nulovou hypotézu uniformity a budeme předpokládat uniformitu, pokud jde o směr příjezdu. Zatímco tento příspěvek byl relativně základním tutoriálem, mnoho lidí v komunitě datových věd nepracovalo s kruhovými daty dříve. Je zajímavým podtémem ponořit se do mladého pole statistiky, které se stále vyvíjí.
závěrečné poznámky
chtěl bych rozšířit kredit na S. Rao Jammalamadaka PhD, University of California, Santa Barbara, a jeho učebnici „témata v Cirkulární statistice“ za vyvolání mého zájmu o oblast cirkulární statistiky.