4.2 odhad koeficientů lineárního regresního modelu / Úvod do ekonometrie S R

4.2 odhad koeficientů lineárního regresního modelu

v praxi nejsou intercept $\beta_0$ a sklon $\beta_1$ populační regresní linie známy. Proto musíme použít data k odhadu obou neznámých parametrů. V následujícím textu bude použit příklad skutečného světa k prokázání toho, jak je toho dosaženo. Chceme spojit výsledky testů s poměrem student-učitel naměřeným v kalifornských školách. Testovací skóre je okresní průměr čtení a matematické skóre pro páté srovnávače. Velikost třídy se opět měří jako počet studentů vydělený počtem učitelů(poměr student-učitel). Pokud jde o data, Kalifornská školní datová sada (CASchools) přichází s balíčkem R s názvem AER, zkratka pro aplikovanou ekonometrii s R (Kleiber and Zeileis 2020). Po instalaci balíčku s instalací.balíčky („AER“) a připojení s knihovnou (Aer) datovou sadu lze načíst pomocí funkce data ().

## # install the AER package (once)## install.packages("AER")## ## # load the AER packagelibrary(AER)# load the the data set in the workspacedata(CASchools)

jakmile je balíček nainstalován, je k dispozici pro použití při dalších příležitostech při vyvolání s knihovnou () – není třeba spouštět instalaci.balíčky () znovu!

je zajímavé vědět, s jakým objektem se zabýváme.class () vrací třídu objektu. V závislosti na třídě objektu se některé funkce (například plot() a shrnutí()) chovají odlišně.

zkontrolujme třídu objektu CASchools.

class(CASchools)#> "data.frame"

ukazuje se, že CASchools má třídní data.rám, který je vhodný formát pro práci s, zejména pro provádění regresní analýzy.

s pomocí head() získáme první přehled o našich datech. Tato funkce zobrazuje pouze prvních 6 řádků datové sady, což zabraňuje přeplněnému výstupu konzoly.

stiskněte ctrl + L pro vymazání konzoly. Tento příkaz odstraní jakýkoli kód, který jste zadali a provedli nebo vytiskli do konzoly pomocí funkcí R. Dobrou zprávou je, že cokoli jiného zůstává nedotčeno. Ani volné definované proměnné atd. ani historie kódu. Stále je možné vyvolat dříve provedené příkazy R pomocí kláves nahoru a dolů. Pokud pracujete v RStudio, stiskněte ctrl + nahoru na klávesnici (CMD + nahoru na Mac) a prohlédněte si seznam dříve zadaných příkazů.

head(CASchools)#> district school county grades students teachers#> 1 75119 Sunol Glen Unified Alameda KK-08 195 10.90#> 2 61499 Manzanita Elementary Butte KK-08 240 11.15#> 3 61549 Thermalito Union Elementary Butte KK-08 1550 82.90#> 4 61457 Golden Feather Union Elementary Butte KK-08 243 14.00#> 5 61523 Palermo Union Elementary Butte KK-08 1335 71.50#> 6 62042 Burrel Union Elementary Fresno KK-08 137 6.40#> calworks lunch computer expenditure income english read math#> 1 0.5102 2.0408 67 6384.911 22.690001 0.000000 691.6 690.0#> 2 15.4167 47.9167 101 5099.381 9.824000 4.583333 660.5 661.9#> 3 55.0323 76.3226 169 5501.955 8.978000 30.000002 636.3 650.9#> 4 36.4754 77.0492 85 7101.831 8.978000 0.000000 651.9 643.5#> 5 33.1086 78.4270 171 5235.988 9.080333 13.857677 641.8 639.9#> 6 12.3188 86.9565 25 5580.147 10.415000 12.408759 605.7 605.4

zjistili jsme, že datová sada se skládá z mnoha proměnných a že většina z nich je číselná.

mimochodem: alternativou k class() A head() je str (), který je odvozen od „struktury“ a poskytuje komplexní přehled o objektu. Zkus to!

když se vrátíme k CASchools, dvě proměnné, které nás zajímají (tj., průměrné skóre testu a poměr student-učitel) nejsou zahrnuty. Je však možné vypočítat jak z poskytnutých údajů. Abychom získali poměr student-učitel, jednoduše vydělíme počet studentů počtem učitelů. Průměrné skóre testu je aritmetický průměr skóre testu pro čtení a skóre matematického testu. Další blok kódu ukazuje, jak mohou být tyto dvě proměnné konstruovány jako vektory a jak jsou připojeny k CASchools.

# compute STR and append it to CASchoolsCASchools$STR <- CASchools$students/CASchools$teachers # compute TestScore and append it to CASchoolsCASchools$score <- (CASchools$read + CASchools$math)/2

kdybychom znovu spustili hlavu (CASchools), našli bychom dvě zajímavé proměnné jako další sloupce s názvem STR a score (zkontrolujte toto!).

tabulka 4.1 z učebnice shrnuje rozdělení výsledků testů a poměrů student-učitel. Existuje několik funkcí, které lze použít k dosažení podobných výsledků, např.,

průměr () (vypočítá aritmetický průměr poskytnutých čísel),
sd () (vypočítá směrodatnou odchylku vzorku),
kvantil() (vrací vektor specifikovaných kvantilů vzorku pro data).

další blok kódu ukazuje, jak toho dosáhnout. Nejprve vypočítáme souhrnné statistiky o sloupcích STR a skóre CASchools. Abychom získali pěkný výstup, shromažďujeme opatření v datech.rám s názvem Distribucesummary.

# compute sample averages of STR and scoreavg_STR <- mean(CASchools$STR) avg_score <- mean(CASchools$score)# compute sample standard deviations of STR and scoresd_STR <- sd(CASchools$STR) sd_score <- sd(CASchools$score)# set up a vector of percentiles and compute the quantiles quantiles <- c(0.10, 0.25, 0.4, 0.5, 0.6, 0.75, 0.9)quant_STR <- quantile(CASchools$STR, quantiles)quant_score <- quantile(CASchools$score, quantiles)# gather everything in a data.frame DistributionSummary <- data.frame(Average = c(avg_STR, avg_score), StandardDeviation = c(sd_STR, sd_score), quantile = rbind(quant_STR, quant_score))# print the summary to the consoleDistributionSummary#> Average StandardDeviation quantile.10. quantile.25. quantile.40.#> quant_STR 19.64043 1.891812 17.3486 18.58236 19.26618#> quant_score 654.15655 19.053347 630.3950 640.05000 649.06999#> quantile.50. quantile.60. quantile.75. quantile.90.#> quant_STR 19.72321 20.0783 20.87181 21.86741#> quant_score 654.45000 659.4000 666.66249 678.85999

pokud jde o ukázková data, používáme plot (). To nám umožňuje detekovat vlastnosti našich dat, jako jsou odlehlé hodnoty, které je těžší objevit při pohledu na pouhá čísla. Tentokrát přidáme některé další argumenty k volání plot().

první argument v našem volání plot (), skóre ~ STR, je opět vzorec, který uvádí proměnné na ose y a x. Tentokrát však tyto dvě proměnné nejsou uloženy v samostatných vektorech, ale jsou to sloupce CASchools. Proto by je R nenalezl, aniž by byla správně zadána data argumentu. údaje musí být v souladu s názvem údajů.rámec, do kterého proměnné patří, v tomto případě CASchools. Další argumenty se používají ke změně vzhledu grafu: zatímco main přidává název, xlab a ylab přidávají do obou OS vlastní štítky.

plot(score ~ STR, data = CASchools, main = "Scatterplot of TestScore and STR", xlab = "STR (X)", ylab = "Test Score (Y)")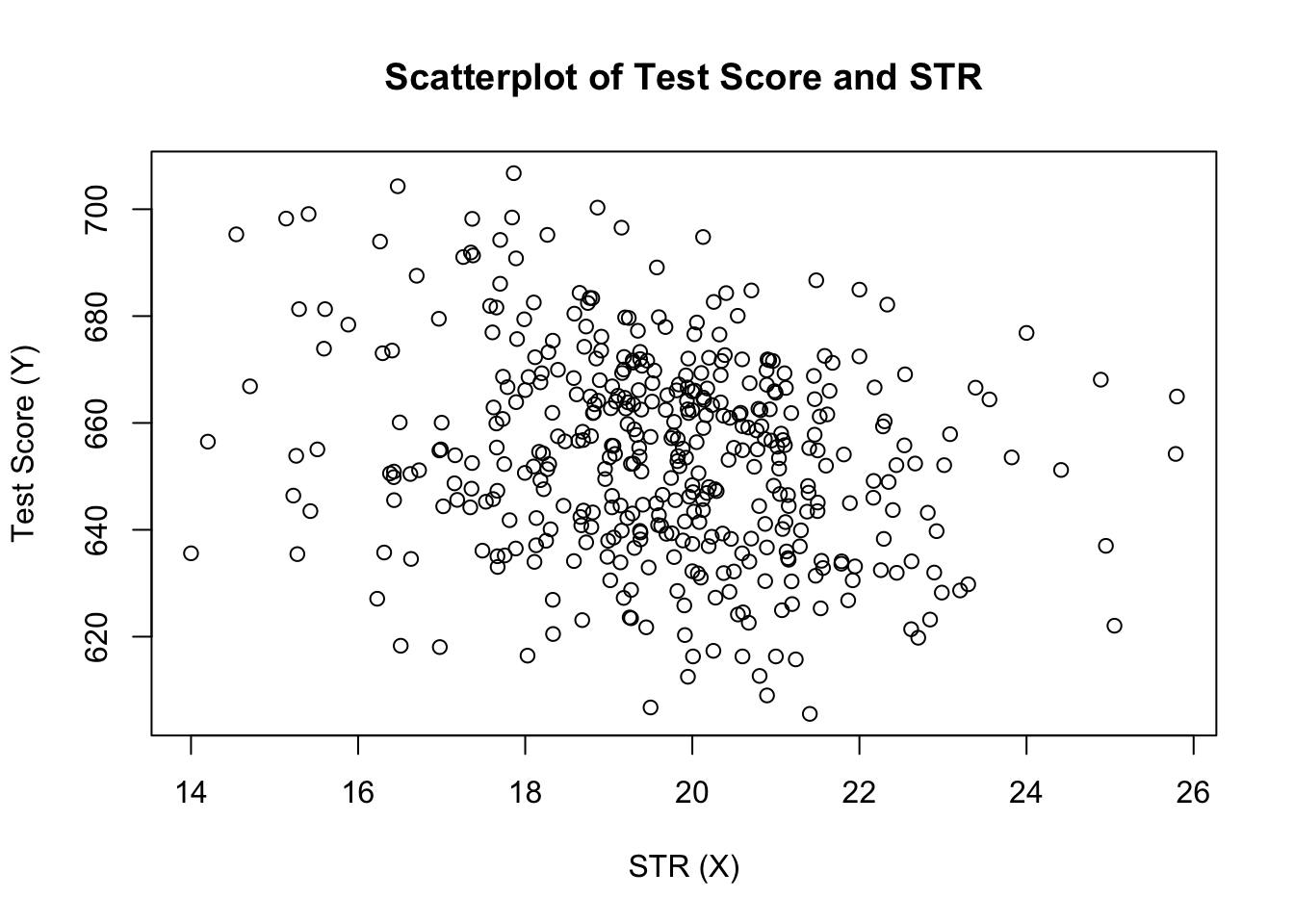

spiknutí (obrázek 4.2 V knize) ukazuje rozptylplot všech pozorování na poměru student-učitel a skóre testu. Vidíme, že body jsou silně rozptýleny a že proměnné jsou negativně korelovány. To znamená, že očekáváme nižší výsledky testů ve větších třídách.

funkce cor () (viz ?cor pro další informace) lze použít k výpočtu korelace mezi dvěma číselnými vektory.

cor(CASchools$STR, CASchools$score)#> -0.2263627

jak již scatterplot naznačuje, korelace je negativní, ale spíše slabá.

úkolem, kterému nyní čelíme, je najít řádek, který nejlépe vyhovuje datům. Samozřejmě bychom se mohli jednoduše držet grafické kontroly a korelační analýzy a poté vybrat nejlepší linii podle oční bulvy. To by však bylo spíše subjektivní: různí pozorovatelé by kreslili různé regresní linie. Z tohoto důvodu nás zajímají techniky, které jsou méně libovolné. Taková technika je dána běžným odhadem nejmenších čtverců (OLS).

běžný odhad nejmenších čtverců

odhad OLS volí regresní koeficienty tak, aby odhadovaná regresní přímka byla co nejblíže pozorovaným datovým bodům. Zde je blízkost měřena součtem kvadratických chyb provedených při předpovídání $Y$ daných $X$. Nechť $b_0$ a $b_1$ jsou některé odhady $\beta_0$ a $\beta_1$. Pak součet chyb odhadu na druhou lze vyjádřit jako

odhad OLS v jednoduchém regresním modelu je dvojice odhadů pro zachycení a sklon, která minimalizuje výše uvedený výraz. Odvození odhadů OLS pro oba parametry je uvedeno v příloze 4.1 knihy. Výsledky jsou shrnuty v klíčovém konceptu 4.2.

odhad OLS, predikované hodnoty a zbytky

odhady OLS sklonu $\beta_1$ a intercept $\beta_0$ v jednoduchém lineárním regresním modelu jsou\předpokládané hodnoty OLS $\widehat{Y}_i$ a rezidua $\hat{u}_i$ jsou\

odhadovaný intercept $\hat{\beta}_0$, parametr sklonu $\hat{\beta}_1$ a zbytky $\Left(\Hat{u}_i\right)$ jsou vypočteny ze vzorku $n$ pozorování $x_i$ a $y_i$, $i$, $…$, $n$. Jedná se o odhady neznámé populace intercept $\left(\beta_0 \right)$, slope $\left (\beta_1\right)$ a error term $(u_i)$.

výše uvedené vzorce nemusí být na první pohled velmi intuitivní. Následující interaktivní aplikace si klade za cíl pomoci vám porozumět mechanice OLS. Pozorování můžete přidat kliknutím do souřadnicového systému, kde jsou data reprezentována body. Jakmile jsou k dispozici dvě nebo více pozorování, aplikace vypočítá regresní čáru pomocí OLS a některé statistiky, které jsou zobrazeny v pravém panelu. Výsledky se aktualizují při přidávání dalších pozorování do levého panelu. Dvojitým kliknutím se aplikace resetuje, tj.

existuje mnoho možných způsobů, jak vypočítat $\hat {\beta}_0$ a $\hat {\beta}_1$ v r.například bychom mohli implementovat vzorce uvedené v Key Concept 4.2 se dvěma nejzákladnějšími funkcemi R: mean() a sum (). Než tak učiníme, připojíme datovou sadu CASchools.

attach(CASchools) # allows to use the variables contained in CASchools directly# compute beta_1_hatbeta_1 <- sum((STR - mean(STR)) * (score - mean(score))) / sum((STR - mean(STR))^2)# compute beta_0_hatbeta_0 <- mean(score) - beta_1 * mean(STR)# print the results to the consolebeta_1#> -2.279808beta_0#> 698.9329

volání attach (CASchools) nám umožňuje adresovat proměnnou obsaženou v CASchools podle jejího názvu: již není nutné používat operátor $ ve spojení s datasetem: R může přímo vyhodnotit název proměnné.

R používá objekt v uživatelském prostředí, pokud tento objekt sdílí název proměnné obsažené v připojené databázi. Je však lepší používat vždy rozlišovací jména, aby se předešlo takovým (zdánlivě) ambivalencím!

Všimněte si, že adresujeme proměnné obsažené v přiloženém datovém souboru CASchools přímo pro zbytek této kapitoly!

samozřejmě existuje ještě více manuálních způsobů, jak tyto úkoly provádět. Vzhledem k tomu, že OLS je jednou z nejpoužívanějších technik odhadu, R již samozřejmě obsahuje vestavěnou funkci s názvem lm() (lineární model), kterou lze použít k provádění regresní analýzy.

prvním argumentem funkce, která má být zadána, je, podobně jako plot(), regresní vzorec se základní syntaxí y ~ x, kde y je závislá proměnná a x vysvětlující proměnná. Argument data určuje soubor dat, které mají být použity v regresi. Nyní se znovu podíváme na příklad z knihy, kde je analyzován vztah mezi skóre testu a velikostí třídy. Následující kód používá lm () k replikaci výsledků uvedených na obrázku 4.3 knihy.

# estimate the model and assign the result to linear_modellinear_model <- lm(score ~ STR, data = CASchools)# print the standard output of the estimated lm object to the console linear_model#> #> Call:#> lm(formula = score ~ STR, data = CASchools)#> #> Coefficients:#> (Intercept) STR #> 698.93 -2.28

přidejte odhadovanou regresní přímku do grafu. Tentokrát také zvětšíme rozsahy obou OS nastavením argumentů xlim a ylim.

# plot the dataplot(score ~ STR, data = CASchools, main = "Scatterplot of TestScore and STR", xlab = "STR (X)", ylab = "Test Score (Y)", xlim = c(10, 30), ylim = c(600, 720))# add the regression lineabline(linear_model)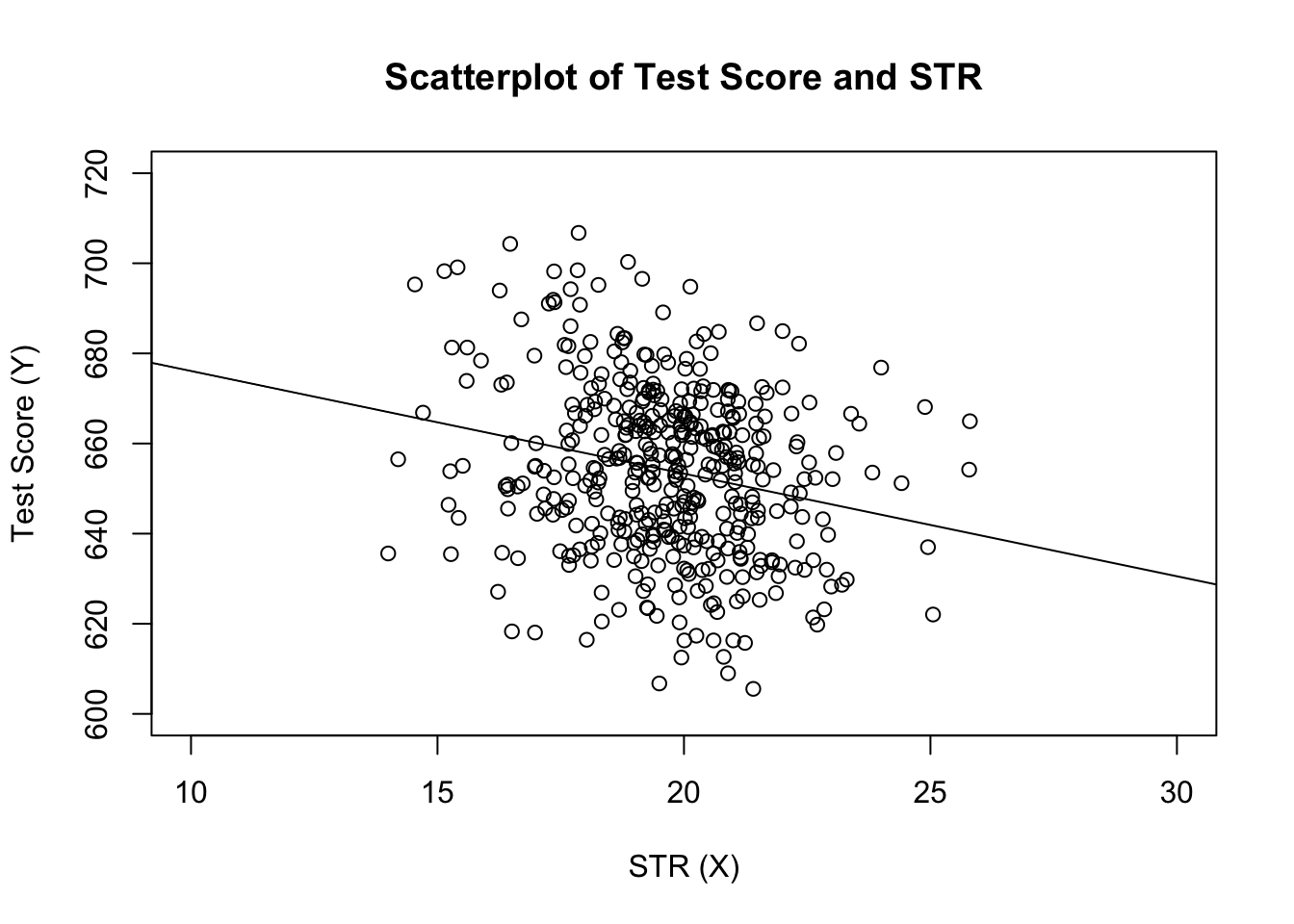

všimli jste si, že tentokrát jsme neprošli parametry zachycení a sklonu do abline? Pokud zavoláte abline() na objekt třídy lm, který obsahuje pouze jeden regresor, R automaticky nakreslí regresní přímku!